Эквивалентность процентных ставок различного типа
Эквивалентные процентные ставки – это такие процентные ставки разного вида, применение которых при одинаковых начальных условиях дает одинаковые результаты.
Приравнивая попарно формулы для определения наращенной суммы, можно получить соотношения, выражающие зависимость между любыми двумя различными процентными ставками.
Приравнивая соотношения 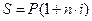 и
и 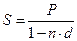 , получим:
, получим:
– простая годовая ставка ссудного процента 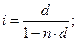
– простая годовая учётная ставка 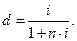
Пример 11.Срок уплаты по долговому обязательству – полгода, учетная ставка равна 18%. Какова доходность данной операции, измеренная в виде простой ставки ссудного процента?
Решение
Используем формулу простой годовой ставки ссудного процента
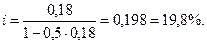
Проверка: 1. При простой процентной ставке 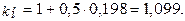
2. При простой учётной ставке 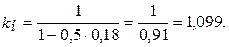
Пример 12.Определить, под какую ставку процентов выгоднее поместить капитал на два года:
а) под простую ставку процентов 20% годовых;
б) под сложную ставку в 16% при ежеквартальном начислении?
Решение
I способ. Найдём простую процентную ставку, эквивалентную данной сложной ставке, воспользовавшись формулой :
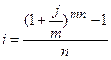 .
. 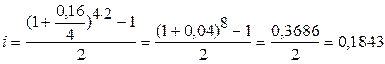 , т.е. 18,43%.
, т.е. 18,43%.
 Так как простая процентная ставка (20%), которая дала бы одинаковый с данной сложной процентной ставкой результат, превышает предложенную (18,43%), ясно, что выгоднее использовать простую процентную ставку.
Так как простая процентная ставка (20%), которая дала бы одинаковый с данной сложной процентной ставкой результат, превышает предложенную (18,43%), ясно, что выгоднее использовать простую процентную ставку.
II способ.Посчитаем коэффициенты наращения, получаемые в обоих случаях: а) под простую ставку процентов 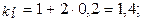
б) под сложную ставку при ежеквартальном начислении
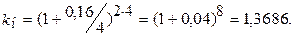
Разница в результатах подтверждает сделанный ранее вывод.
Аннуитеты
В большинстве современных коммерческих операций подразумеваются не разовые платежи, а последовательность денежных поступлений (или, наоборот, выплат) в течение определенного периода. Такая последовательность называется потоком платежей.
Поток платежей, все элементы которого распределены во времени так, что интервалы между любыми двумя последовательными платежами постоянны, называют аннуитетом,или финансовой рентой.
Аннуитет, для которого платежи осуществляются в начале соответствующих интервалов, носит название аннуитета пренумерандо;если же платежи осуществляются в конце интервалов, мы получаем аннуитет постнумерандо (обыкновенныйаннуитет) – пожалуй, самый распространенный случай. Такой аннуитет предполагает получение или выплаты одинаковых по величине сумм на протяжении всего срока операции в конце каждого периода (года, полугодия, квартала, месяца и т.д.).
Введем следующие обозначения:
Р –величина каждого отдельного платежа;
iс – сложная процентная ставка, по которой начисляются проценты;
Sk – наращенная сумма для k-го платежа аннуитета постнумерандо;
S – наращенная (будущая) сумма всего аннуитета постнумерандо (т. е. сумма всех платежей с процентами);
Ak – современная величина к-го платежа аннуитета постнумерандо;
А –современная величина всего аннуитета постнумерандо.
п – число платежей.
