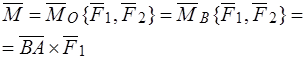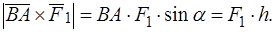Общий признак эквивалентности двух систем сил (критерий эквивалентности)

Теорема. Для того, чтобы две системы сил были эквивалентны, необходимо и достаточно, чтобы у этих систем были геометрически равны соответственно главные векторы и главные моменты относительно одного и того же полюса.

Доказательство.

Необходимость.

Дано: .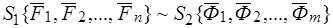

Следует доказать, что у этих систем сил равны главные векторы и главные моменты относительно одного и того же полюса, то есть что

, .

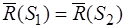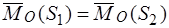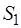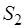Доказательство: Системы сил и эквивалентны, следовательно, одна из другой могут быть получены с помощью элементарных операций. Но элементарные операции не изменяют главный вектор и главный момент системы сил – второе (геометрическое) свойство элементарных операций, поэтому , .

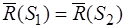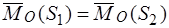Достаточность.

Дано: две системы сил 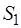и 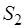, главные векторы и главные моменты которых равны, то есть , .

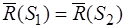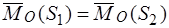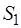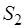Доказать, что системы и эквивалентны.

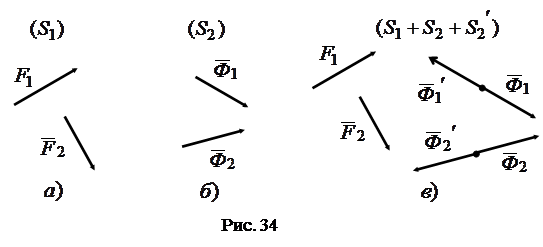Доказательство: Не ограничиваясь в общности, проводим доказательство в предположении, что каждая из систем 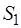и 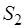состоит из двух сил, то есть пусть даны системы сил 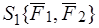и 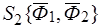(рис 34а). В силу основной леммы статики системы сил 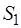и 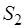, содержащие произвольное число сил всегда при помощи элементарных операций могут быть приведены к двум силам, при этом главные векторы и главные моменты этих систем сил не изменяются.

Рассмотрим дополнительную систему 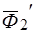, силы которой пряморотивоположны силам системы :

, .

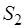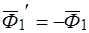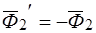Тогда , .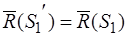

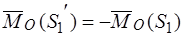Системы сил 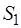(рис. 34а) и 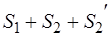(рис. 34в) эквивалентны:

,

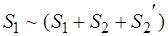так как система 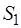может быть получена из системы 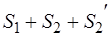отбрасыванием прямопротивоположных сил 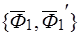и .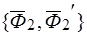

Рассмотрим систему 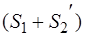, состоящую из сил .

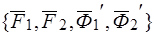Главный вектор: .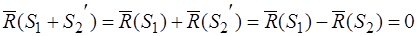

Главный момент:

.

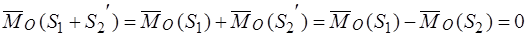Согласно основной лемме статики систему сил 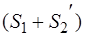можно заменить двумя силами 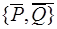. Тогда 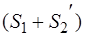~ 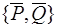. У эквивалентных систем сил равны главные моменты и главные вектор: поэтому

,

,

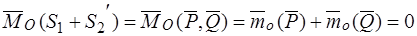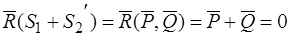то есть 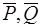– прямопротивоположные силы, которые можно отбросить. Таким образом:

,

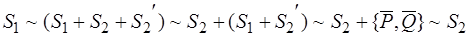или .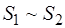

Теорема доказана.

ТЕОРИЯ ПАР СИЛ

Момент пары сил

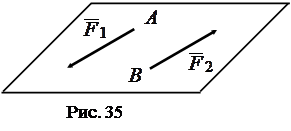Рассмотрим пару сил 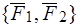. По определению – это совокупность двух равных по величине и параллельных сил, направленных в противоположные стороны (рис. 35).

Плоскость, в которой лежит пара сил, называется плоскостью пары. Как уже отмечалось, главный момент пары не зависит выбора полюса и отличен от нуля.

Главный момент пары, не зависящий от выбора полюса, называется моментом пары. Обозначение: 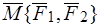, или .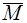

Момент пары – это свободный вектор, перпендикулярный плоскости пары, направленный в ту сторону, откуда видно, что пара стремится вращать тело против часовой стрелки, и равный по величине произведению одной из сил пары на кратчайшее расстояние между линиями действия сил пары (плечо пары).

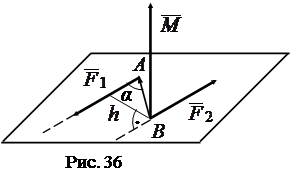Для доказательства этого утверждения рассмотрим пару 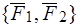(рис. 36).