Реальная и номинальная ставка

Различают номинальную и реальную процентную ставку.

Реальная процентная ставка — это процентная ставка, очищенная от инфляции.

Взаимосвязь реальной, номинальной ставки и инфляции в общем случае описывается следующей (приближённой) формулой:

i_r = i_n − π

где:

· i_n — номинальная процентная ставка

· i_r — реальная процентная ставка

· π — ожидаемый или планируемый уровень инфляции.

Ирвинг Фишер предложил более точную формулу взаимосвязи реальной, номинальной ставок и инфляции, выражаемую названной в его честь формулой Фишера:

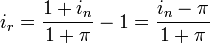
При небольших значениях уровня инфляции π результаты мало отличаются, но если инфляция велика, то следует применять формулу Фишера.

Пример.Кредит выдан банком под 30% годовых, планируемый уровень инфляции 15% годовых. Определить реальную процентную ставку.

Решение:

i_r = 30-15 = 15(%)

i_r = (1+0,3)/(1+0,15)-1=0,13 или 13%

Правило 72. Если процентная ставка есть a, то удвоение капитала по такой ставке происходит примерно за 72/a лет. Это правило применяется для небольших ставок, вычисляемых по сложным процентам.

Пример. Годовая ставка сложных процентов равна 8%. Через сколько лет начальная сумма удвоится? Решение: 72/8=9 лет

Оценка реальной эффективности кредитно-депозитных операций с учётом инфляции

Пример. Вклад в сумме 20 000 рублей положен в банк на 6 месяцев с ежемесячным начислением сложных процентов по ставке 15% годовых. Уровень инфляции составляет 0,7% в месяц.

Определить сумму вклада с процентами, индекс инфляции за 6 месяцев, сумму вклада с процентами с точки зрения покупательной способности, реальный доход вкладчика с точки зрения покупательной способности. При каком уровне инфляции вклад не принесет реального дохода?

Решение

S=20000∙(1+0,15/12)⁶ =21547

I=(1+i)⁶ =(1+0,007)⁶ =1,0427

К= 21547/ 1,0427=20664

Д=20664-20000=664

I = 21547/20000=1,07835 i= 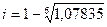= 0,0125= 1,25%

Пример. Банк выдал кредит 900 тыс. руб. на год под 13% годовых простых процентов. Ожидаемый уровень инфляции 7% годовых. Определить с учётом инфляции: реальную ставку процентов по кредиту,погашаемую сумму, сумму реального дохода банка, очищенную от инфляции

Решение:

13-7 = 6%

900000(1+0,13)=1017000 руб.

1017000/1,07=950467 руб.

950467-900000=50467 руб.

В случае ежегодного начисления процентов для лица, предоставляющего кредит:

1) Более выгодной является схема простых процентов, если срок ссуды менее одного года (проценты начисляются однократно в конце периода);

2) Более выгодной является схема сложных процентов, если срок ссуды превышает один год (проценты начисляются ежегодно);

3) 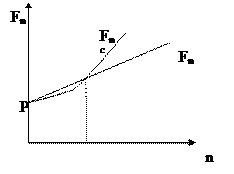Обе схемы дают одинаковые результаты при продолжительности периода 1 год и однократном начислении процентов.

Годовая эффективная ставка r_ef используется для сравнительного анализа эффективности контрактов, является универсальным показателем для любой схемы начисления. Она показывает, какую годовую ставку сложных процентов необходимо установить, чтобы получить такой же финансовый результат, как и при m-разовом начислении процентов в году по ставке r^(m)/m.

r_ef =(1+r^(m)/m)^m-1.

Пример. Предприниматель может получить ссуду а) либо на условиях ежемесячного начисления процентов из расчета 26% годовых, б) либо на условиях полугодового начисления процентов из расчета 27% годовых. Какой вариант предпочтительнее?

Решение:

Для варианта а) r_ef=(1+0,26/12) ¹² -1=0,2933;

Для варианта б) r_ef=(1+0,27/2) ²-1=0,2882 – данный вариант предпочтительнее.