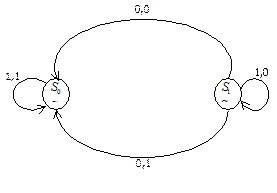
Покрытие и эквивалентность

Теория конечных автоматов

Введение.

Теория конечных автоматов исследует тематические модели, приближенно отражающие физические или абстрактные явления, причем эти модели могут быть из области психологии, административного управления, связи, лингвистики, теории ЭВМ и т.д. С помощью конечных автоматов можно исследовать нервную систему животных или человека и проектировать ЭВМ.

Универсальная ЭВМ состоит из 5 устройств:

1) устройство ввода;

2) устройство памяти;

3) арифметическое устройство;

4) устройство управления;

5) устройство вывода.

Дискретный автомат будем трактовать как устройство (реальное или абстрактное) осуществляющее прием, хранение и преобразование дискретной информации по некоторому правилу (алгоритму). Примером автомата могут служить ЭВМ, математические абстрактные машины, аксиоматические теории и т.п.

Общую теорию автоматов подразделяют на абстрактную и структурную. Абстрактная теория, отвлекаясь от реальной структуры автомата, его элементной базы и способов построения, изучает только поведение автомата относительно поведения внешней среды. Тем самым можно говорить только о том, что абстрактная теория автоматов близка к теории алгоритмов. Структурная теория автоматов учитывает и интересуется как структурой самого автомата, так и структурой входных воздействий и реакции автомата на них. В структурной теории изучаются способы построения автоматов, способы кодирования входных воздействий и выходных сигналов (реакций).

Последовательность действий машины определяется программой, которая выполняется последовательно. Сама программа может предусматривать пропуск или повторение информации, хранящейся в памяти, т.е. от внутреннего состояния машины.

ЭВМ бывают цифровые и аналоговые. Мы здесь рассматриваем цифровые. Все сигналы в такой машине двузначны, т. е. принимают значения из множества .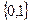

Материальные носители и преобразования сигналов – конечны. Множество состояний любой машины также конечно.

Определение автомата Мили.

Автомат Мура.

Определение:Конечным автоматом называется набор из 5 объектов 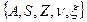, где:

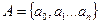- входной алфавит;

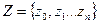­ выходной алфавит;

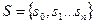­ множество внутренних состояний;

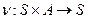­ функция перехода (в следующее состояние);

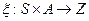­ функция выхода.

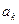Таким образом, конечный автомат описывается тремя множествами и двумя функциями. Обе функции зависят от текущего внутреннего состояния и от входного символа, считываемого в данный момент времени. Автомат действует следующим образом. Конечный автомат, находящийся во внутреннем состоянии , считывает входной символ . Функция 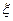принимает на паре 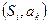значение 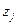- первый символ выхода. Функция 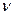принимает на паре 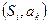значение 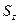, которое является следующим внутренним состоянием.

Пусть входящие символы записаны на входной ленте: **********. Автомат считывает с нее символы один за другим. По прочтению каждого символа автомат печатает выходной символ на выходной ленте и переходит в новое внутреннее состояние.

В определении подразумевается, что функци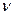и и 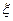в описании автомата М всюду определены, т.е. каждая пара из прямого произведения 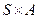задает их значения. Такое описание автомата является полным, т.е. если задано начальное состояние автомата, то он способен считывать любую последовательность входных символов и выдавать однозначно определенную цепочку символов на выходе.

Конечный автомат считается заданным, если заданы множества 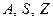(конечные), а также даны функции или приведено их описание. Существует три способа задания конечных автоматов: таблица, диаграмма и матрица переходов.

Пример 1. Конечный автомат задан следующим образом:

, , , .

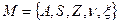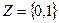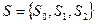Значения функций 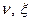заданы таблицей:

n:	(S0, 0)®S1,	x:	(S0, 0)®0,
	(S0, 1)®S0,		(S0, 1)®1,
	(S1, 0)®S2,		(S1, 0)®1,
	(S1, 1)®S1,		(S1, 1)®0,
	(S2, 0)®S0,		(S2, 0)®1,
	(S2, 1)®S2,		(S2, 1)®0.

Пусть на входе дана двоичная последовательность 0101 и автомат находится в состоянии 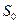, тогда на выходе получаем последовательность: 0010.

Этот автомат можно наглядно представить в виде диаграммы, которая, по сути, является ориентированным графом.

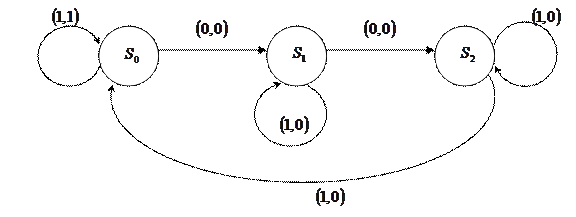Вершины этого графа помечены символами, обозначающими внутреннее состояние. Каждая дуга помечено парой символов (метка) 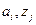, где 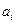- входной символ, вызывающий переход в следующее состояние, а 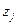- символ на выходе.

Второй способ описания автомата – таблица состояний. Этот способ часто приводится в виде условия задачи. Это просто табличное представление функци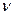й и :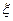

Текущее состояние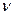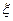

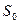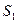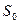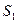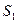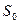Таблица удобнее для вычислений, диаграмма - нагляднее. Например, по диаграмме легко обнаружить состояния, не достижимые из других состояний.

Кроме того, автомат можно задать с помощью матрицы. Такая матрица всегда будет квадратной по форме, а размерность её зависит от количества внутренних состояний. Каждая позиция матрицы отвечает за определённый переход из одного состояния в другое. Если какой-то переход существует, то на определённом месте матрицы должна стоять соответствующая метка. Если же некоторый переход отсутствует, то на этом месте в матрице стоит ноль.

Пример 2. По приведенному описанию построить конечный автомат. Задать его таблицей и диаграммой. Данный автомат проверяет четность числа считываемых единиц на входе из последовательности нулей и единиц, и выводит на печать символы чёт и нечёт в ответ на запрос, которому соответствует входной символ Q.

Согласно условию, алфавит на входе: 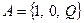, алфавит на выходе состоит из символов: 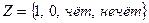. Множество внутренних состояний: 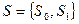, где содержание этих состояний следующее: 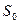- считано четное число единиц; 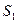- считано нечетное число единиц.

Анализируя работу автомата, можно составить таблицу:

Текущее состояние	n	x
		Q			Q
S0	S0	S1	S0			чёт
S1	S1	S0	S1			нечёт

Считав символ Q, автомат печатает "чет", если число ранее считанных единиц было четно, и "нечет" - если нечетно. Например, входная последовательность символов имела вид: 0110Q1110Q. Она будет переработана в последовательность: 0110четн1110нечет.

Диаграмма для данного автомата может быть составлена с помощью построенной таблицы:

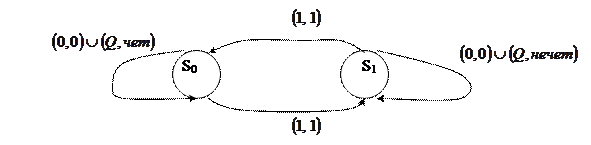
Любой конечный автомат Мили может быть преобразован в автомат, в котором выходной символ является функцией только состояния в настоящий момент.

Для этого полагают 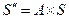- новый алфавит, 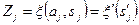, 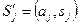. Отсюда получаем выражение для 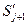: 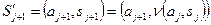или .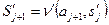

Такой автомат называется автоматом Мура. Так как автоматы Мили и Мура можно преобразовать друг в друга, то обычно достаточно рассматривать автомат Мили, тем более что число состояний у него меньше, чем у соответствующего автомата Мура.

Покрытие и эквивалентность.

Морфизмы.

Пусть 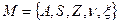- конечный автомат. Тогда по любой входной строке 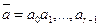длины r и по любому начальному состоянию 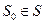однозначно определяется строка длины r внутренних состояний 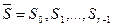, которая получается последовательным применением отображения 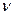. Точнее: 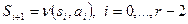. Аналогично строка на выходе определяется последовательным применением отображения 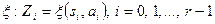. Поэтому рассмотрим автомат как устройство, перерабатывающее пары, состоящие из состояния 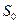и 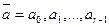в строк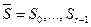и и 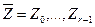. С помощью функци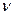й и 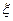можно определить функции 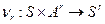, , 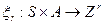которые строятся по функциям 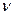и 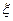, заданным в описании автомата М.

Пример. Автомат задан диаграммой:

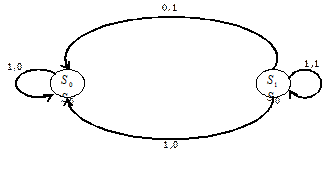
Пусть входная строка 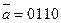и начальное состояние 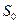, тогда _, .

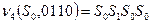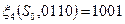Увеличение числа внутренних состояний автомата в реальном устройстве приводит к росту количества электронных схем, к уменьшению надежности, к усложнению отладки и т. д. Поэтому число необходимых состояний автомата, предназначенного для выполнения определенных действий, стремятся уменьшить, не ограничивая его возможностей.

Этим объясняется важность следующей задачи. Предположим, что входной и выходной алфавиты фиксированы. Возникает следующий вопрос. Можно ли заменить автомат 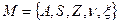автоматом с меньшим числом внутренних состояний 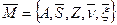, но с той же функцией, переводящей входы в выходы?

Определение 1: Говорят, что автомат 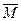покрывает автомат 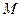, если входной и выходной алфавиты у них общие и существует функция 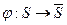, такая что для любого положительного числа 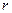имеет место условие:

.

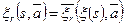
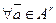Определение 2: Автомат, который нельзя покрыть меньшим автоматом, называется минимальным. Будем писать: 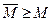, если 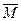покрывает .

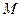Теорема 1: Отношение покрытий рефлексивно и транзитивно.

Доказательство очевидно.

Определение 3: Автоматы 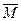и 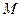называются эквивалентными, если автомат 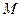покрывает 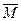и автомат 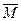покрывает 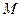. В этом случае пишут: .

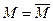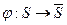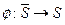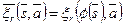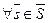Это означает, что кроме функции со свойством, указанным в предыдущем определении, существует еще функция со следующим свойством: при и .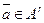

Следствие: Отношение эквивалентности автоматов рефлексивно, транзитивно и симметрично.

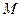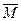Пусть и – автоматы с общими входными и выходными алфавитами.

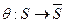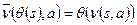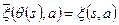
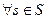Определение 4:Морфизмом называется такое отображение , что и и 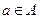. Если 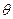сюрьективно, то морфизм называется эпиморфизмом. Если 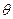- биекция, то морфизм называется изоморфизмом.

Теорема 2: Пусть 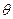эпиморфизм автомат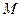а на 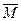. Тогда для любой входной строки 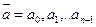и любого начального состояния 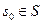входная строка 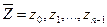автомата 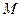совпадает с входной строкой автомата 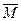, если начальное состояние 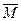равно .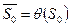

Доказательство:Доказательство можно провести индукцией по числу 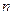с индуктивным шагом:

;

.

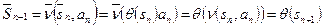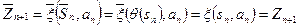Следствие: Любой эпиморфизм 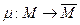определяет покрытие автомата 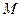автоматом 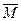. Изоморфизм автоматов 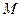и 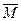с общим входным и выходным алфавитами есть биекция 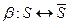, такая, что для всякого начального состояния 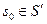и всякой входной строки 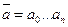автоматы 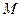и 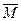выдают одну и ту же выходную строку, проходя через соответствующие промежуточные состояния.

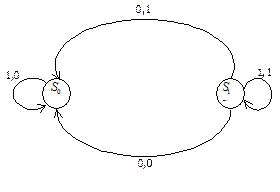
Пример. Автоматы, представленные следующими ориентированными графами, изоморфны.