Определение параметров аннуитета

Последовательные платежи в виде постоянной обычной годовой ренты определяются основными параметрами:

R – размер платежа;

n – срок ренты в годах;

i – годовая ставка процентов.

Однако при разработке условий финансовой операции могут возникать ситуации, когда заданной величиной является одна из двух обобщающих характеристик и неполный набор параметров ренты.

В таких случаях находят недостающий параметр.

При определении члена ренты возможны два варианта, зависящие от того, какая величина является исходной:

а) наращенная сумма.

Если сумма долга определена на какой-либо момент в будущем (FVA), тогда величину последующих взносов в течение n лет при начислении на них процентов по ставке i можно определить по формуле:

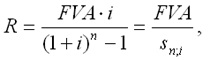Пример:

Для покупки автомобиля через 5 лет потребуется 50 тыс. руб.

Определите размер ежегодных взносов, вносимых в конце каждого года в банк, который начисляет проценты по ставке 40%.

Решение:

В данном случае известна наращенная величина постоянной финансовой ренты, поэтому размер ежегодных взносов будет равен:

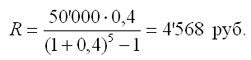Таким образом, чтобы накопить на счете необходимую сумму для покупки автомобиля следует в конце каждого года в течении пяти лет откладывать 4'568 руб.

б) современная величина финансовой ренты, тогда, исходя из ставки процента и срока ренты, разовый платеж находится по формуле:

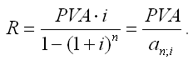Пример:

Сумма 10 тыс. долларов предоставлена в долг на 5 лет под 8% годовых.

Определить ежегодную сумму погашения долга.

Решение:

Известна современная величина долга, отсюда:

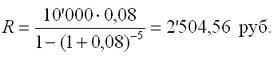Таким образом, ежегодно необходимо будет возвращать сумму 2'504,56 руб.

Можно произвести проверку: сумма долга с начисленными на нее процентами к концу пятого года будет составлять:

FV = 10'000 • (1 + 0,08)⁵ = 14'693,28 руб.

Наращенная сумма для потока платежей размером 2'504,56 руб. составит:

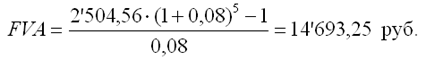Следовательно, величина члена финансовой ренты определена верно.

Незначительное расхождение вызвано округлением расчетов.

Современная величина ренты пренумерандо рассчитывается путем умножения современной величины обычной ренты на соответствующий множитель наращения.

Оценка некоторых видов аннуитета.

Бессрочный аннуитет.

Если денежные поступления осуществляются достаточно длительное время и их число заранее не может быть известно, то такой поток называется бессрочным аннуитетом или вечной рентой.

В этом случае определение будущей величины такого аннуитета не имеет смысла.

Для данного вида финансовой ренты имеет смысл только характеристика современной величины потока платежей.

Поток, даже с неограниченным числом платежей все же имеет конечную приведенную стоимость, поскольку с финансовой точки зрения, деньги, поступающие через много лет, сейчас практически ничего не стоят.

Для бессрочного аннуитета постнумерандо формула современной величины принимает следующий вид:

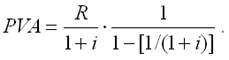При больших сроках аннуитета и большом уровне процентной ставки для определения приведенной величины срочного аннуитета можно пользоваться формулой бессрочного аннуитета, поскольку полученный приблизительный результат не слишком будет отличаться от точного значения, т.к. при сроке более 40-50 лет коэффициенты дисконтирования аннуитета незначительно отличаются друг от друга.

Приведенная стоимость бессрочного аннуитета пренумерандо в общем виде определяется из приведенной стоимости бессрочного аннуитета постнумерандо, скорректированного на коэффициент (1 + i), т.е. отличается на величину первого платежа.

Непрерывный аннуитет.

Если промежутки между последовательными поступлениями являются бесконечно малой величиной, то такой аннуитет считают непрерывным, т.е. денежные поступления происходят непрерывно с постоянной интенсивностью.

При начислении непрерывных процентов для получения формул определения наращенной или современной величины потока платежей необходимо перейти к пределу, откуда:

· наращенная величина потока платежей

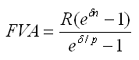где

σ – сила роста.

· современная величина потока платежей
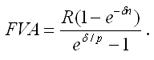