Указания к выполнению задания 15
Премия за риск (ПР):
ПР = b (СНД - БНД),
где БНД — безрисковая норма доходности на рынке финансовых инструментов;
b — фактор «бета»;
СНД — средняя норма доходности на рынке финансовых инструментов.
ПРВ = b (СНД - БНД)=1,9(13,2-7)=11,78
ПРА = b (СНД - БНД)=1,2(16,2-5)=13,44
ПРО = b (СНД - БНД)=1,5(9,4-5)=6,6
ПР Д= b (СНД - БНД)=0,7(3,4-2)=0,98
Значение b «бета» говорит, что любое небольшое изменение средней доходности приведет к значительным изменениям в их доходности, а следовательно, премия за риск должна быть выше.
Требуемая доходность по каждому инвестиционному инструменту (ТД):
ТД = БНД +ПР или БНД +b (СНД - БНД).
ТДВ = БНД +ПР=7+11,78=18,78
ТДА = БНД +ПР=5+13,44=18,44
ТД = БНД +ПР=5+6,6=11,6
ТД = БНД +ПР=2+0,98=2,98
Как правило, чем выше значение фактора b «бета», тем выше рискованность проекта, а следовательно, больше размер премии за риск должен брать инвестор, чтобы покрыть свой риск. Проводя сравнение по каждому из инвестиционных инструментов, можно будет сделать предложения по наиболее предпочтительному финансовому инструменту.
Вывод: на основании проведенных расчетов можно сделать вывод, что наиболее предпочтительным финансовом инструментом вложения средств – акции, т.к. при значении коэффициента b - 1,2, т.е. с риском меньше векселя (1,9), средняя норма доходности выше на 3%, премия за риск в этом случае выше у акций. Риск по депозитному счету, значительно ниже, чем при остальных операциях, однако норма доходности очень низка.
Задание 16
Директор строительной организации _Самарадорстрой_ не может принять решения по выбору наиболее эффективного варианта инвестиционного вложения. Варианты развития событий представлены в исходных данных. Помогите руководителю организации принять правильное решение, с учетом фактора риска, используя методику расчета средневзвешенной эффективности по критерию Гурвица.
Расчеты проведите, используя исходные данные таблицы 23. Оформите полученные расчеты в виде таблицы 24.
Требуется:
1. Альфа-коэффициент, принимаемый с учетом рискового предпочтения в поле от 0 до 1;
2. Определить минимальное и максимальное значение эффективности по конкретной альтернативе;
3. Выбрать наибольшее значение средневзвешенной эффективности по критерию Гурвица для конкретной альтернативы.
Таблица 23 - Основные исходные данные для задания 16
| Вариант альтернативных решений | Эффективность в зависимости от варианта развития событий, тыс.р. | |||
| Э1 | Э2 | Э3 | Э4 | |
| 1. Приобрести программный продукт | ||||
| 2. Воспользоваться услугами сторонней организации | ||||
| 3. Увеличить численность экономического отдела |
Таблица 24 - Выбор оптимального рискового решения по критерию Гурвица
| Варианты альтернативных решений | a | Эмахi | a* Эмахi | (1-a) | Эмini | (1-a)Эмiхi | Аi |
| 0,5 | 0,5 | ||||||
| 0,5 | 0,5 | ||||||
| 0,5 | 0,5 |
Указания к выполнению задания 16
Критерий Гурвица (критерий «оптимизма-пессимизма» или «альфа -критерий») (Аi):
Аi=a* Эмахi+(1-a)Эмini,
где Аi — средневзвешенная эффективность по критерию Гурвица для конкретной альтернативы;
a - альфа-коэффициент, принимаемый с учетом рискового предпочтения в поле от 0 до 1;
Эмахi - максимальное значение эффективности по конкретной альтернативе;
Эмiхi - минимальное значение эффективности по конкретной инициативе.
Принимая значениеальфа-коэффициента равным 0,5, можно говорить о том, что субъект нейтрален к риску. Вариант считается наиболее приемлемым там, где средневзвешенная эффективность будет наибольшей.
Вывод: на основании проведенных расчетов можно сделать вывод, что наиболее предпочтительным будет вариант № 2, т.к. Аi имеет наибольшее значение.
Задание 17
Предприятие проводит оценку рискованности будущего инвестиционного проекта по строительству торгового центра на основе метода «дерева решений» или «дерева вероятности». В качестве основного показателя эффективности проектов избран чистый приведенный доход. Срок реализации по проекту составляет два года – он разбит на два этапа реализации, продолжительность которых принята по одному году. Определена система возможных альтернативных решений по отдельным этапам их реализации, рассчитана вероятность таких решений и сумма чистого приведенного дохода в настоящей стоимости по каждому из рассматриваемых альтернатив, которые отражены на «дереве решений», представленном в исходных данных (рисунок 1).
Оформите полученные расчеты в виде таблиц 25 и 26.
Требуется:
1. Провести расчет средневзвешенной вероятности и суммы чистого приведенного дохода.
2. Рассчитать дисперсию и среднеквадратическое отклонение показателя чистого приведенного дохода.
3. Определить коэффициент вариации или уровень риска.
4. Дать оценку рискованности будущего инвестиционного проекта.
Таблица 25 - Расчет средневзвешенной вероятности и суммы чистого приведенного дохода
| Номер альтернативных решений | Альтернативная сумма чистого приведенного дохода, млн. р. | Вероятно-сти | Расчет средневзвешен-ной вероятности | Расчет средневзвешенной суммы чистого приведенного дохода, млн.р. | |
| 1-й год | 2-й год | ||||
| 0,2 | 0,1 | 0,02 | 5,2 | ||
| 0,2 | 0,6 | 0,12 | 25,92 | ||
| 0,2 | 0,3 | 0,06 | |||
| 0,7 | 0,2 | 0,14 | 26,88 | ||
| 0,7 | 0,5 | 0,35 | 61,6 | ||
| 0,7 | 0,3 | 0,21 | 34,44 | ||
| 0,1 | 0,3 | 0,03 | 4,32 | ||
| 0,1 | 0,5 | 0,05 | 6,2 | ||
| 0,1 | 0,2 | 0,02 | 2,08 | ||
| ИТОГО | 178,64 |
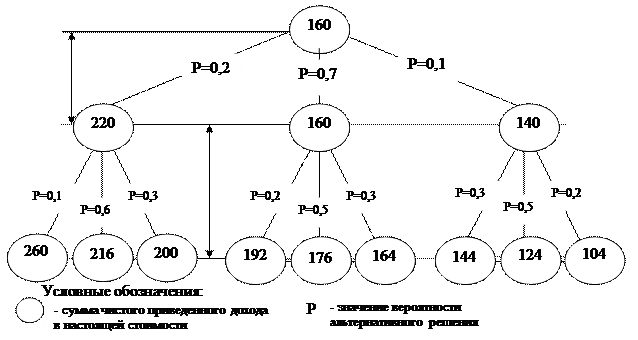
Рисунок 1- «Дерево решений»
Таблица 26 - Расчет среднеквадратического отклонения и коэффициента вариации по результатам построения «дерева решений»
