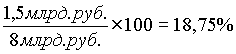Определение чистой настоящей стоимости и внутренней ставки доходности инвестиционного проекта в инфляционной среде сопряжено со значительными трудностями

Ниже дана универсальная формула вычисления чистой настоящей стоимости (NPV) проекта, позволяющая оценить эту величину в случае неодинакового инфляционного искажения доходов и затрат. Формула удобна тем, что позволяет одновременно производить и инфляционную коррекцию денежных потоков, и дисконтирование на основе средневзвешенной стоимости капитала, включающей инфляционную премию.

где R_t — номинальная выручка 1-го года, оцененная для без инфляционной
ситуации, т.е. в ценах базового периода;
i_r — темпы инфляции доходов t-го года;
C_t — номинальные денежные затраты t-гo года в ценах базового периода;
i’_r — темпы инфляции издержек r-го года;
Т — ставка налогообложения прибыли;
I_{о — первоначальные затраты на приобретение основных средств;}
k — средневзвешенная стоимость капитала, включающая инфляционную
премию;
D_t — амортизационные отчисления t-гo года.

Далее, внутренняя ставка рентабельности (IRR) проекта представляет собой ту ставку дисконтирования, при которой чистая настоящая стоимость проекта равна нулю (все затраты, с учетом временной стоимости денег, окупаются).

* Приводимая здесь формула основана на вычислении чистого денежного потока как (R-С)(1-Т)+ОТ, где К— выручка, С — денежные затраты, D — амортизационные отчисления, Т — ставка налогообложения прибыли. Нетрудно убедиться, что эта модель чистого денежного потока идентична той, что приводится во всех учебниках по инвестиционному анализу (чистая прибыль плюс амортизационные отчисления): (R - 0(1-Т)+ DT = R-C- RT + ТС + DT -D+D = (R-С- D)(l -Т)+D.

Для определения IRR графическим методом (см. задание 3) нужно:
1. Задать некую ставку дисконтирования и определить NPV проекта. Отметить соответствующую точку на графике (по оси ординат — ставка доходности, дисконтирования, по оси абсцисс — NPV).
2. Задать гораздо большую ставку дисконтирования (тогда NPV резко уменьшится), вычислить NPV и отметить соответствующую точку на графике.
3. Соединить данные две точки и, если необходимо, продлить график NPV до пересечения с осью IRR. В ТОЧКЕ ПЕРЕСЕЧЕНИЯ ГРАФИКА NPV С ОСЬЮ IRR ЧИСТАЯ НАСТОЯЩАЯ СТОИМОСТЬ ПРОЕКТА РАВНА НУЛЮ. Это, конечно, очень неточный способ ибо по идее наш график не должен быть строго прямой линией.

Задание.3 разделу 2.1.

Пользуясь значением средневзвешенной стоимости капитала, вычисленным в задании 1, а также данными по инвестиционному проекту, приведенными ниже, определите чистую настоящую стоимость и внутреннюю ставку рентабельности проекта. Затем, сравнив последнюю со средневзвешенной стоимостью капитала, сделайте вывод о целесообразности (либо нецелесообразности) осуществления данного проекта.

Первоначальные затраты на проект 8 млрд. руб.
Срок жизни проекта 4 года
Ежегодные амортизационные отчисления 2 млрд. руб.
Ставка налогообложения прибыли 38%
Средневзвешенная стоимость капитала,
включающая инфляционную премию 250%

Поступления и затраты в ценах
базового периода, млрд, руб.

Годы	Поступления	Затраты

* Это подлинный пример 1995 года.

Прогнозируемый уровень инфляции

Годы	Поступления	Затраты
	300% 220% 150% 80%	200% 180% 120% 100%

Решение к заданию 3 раздела 2.1.

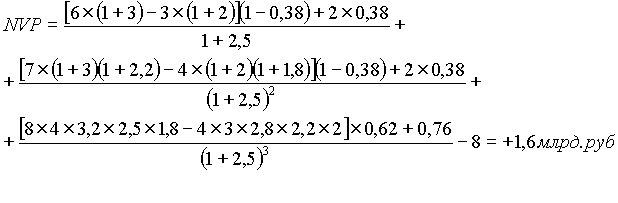
Где, NPV- чистая настоящая стоимость проекта

Таким образом, при ставке дисконтирования 2,5 (250%) чистая настоящая стоимость проекта (1,6 млрд. руб.) положительна. Это означает, что проект способен обеспечить выраженные в средневзвешенной стоимости капитала интересы и ожидания инвесторов и кредиторов.
Но констатации того факта, что NPV больше нуля, еще недостаточно для окончательного вывода о целесообразности осуществления проекта. Необходимо знать, превышает ли IRR средневзвешенную стоимость капитала.

Задаем ставку дисконтирования, к примеру, 6,5 и вычисляем чистую настоящую стоимость проекта. Она равна 5,696 млрд. руб. (Проверьте, пожалуйста, свой результат. Чистая настоящая стоимость проекта стала отрицательной вследствие завышенной “цены капитала” предприятия).

3. Отмечаем на графике соответствующие точки, соединяем их и видим, что NPV == 0 при IRR = 3,3. Это значительно больше ССК.

Правильность выбора данного проекта не оставляет больше сомнений. Секрет успеха рассматриваемого проекта явно заключается в возможности производителя повышать цены готовой продукции опережающими темпами по сравнению с инфляционным ростом цен издержек и, таким образом, не только перекладывать повышение затрат на потребителя, но и снимать значительную прибыль.

Примечание.
1. Срок жизни проекта — это период (количество лет), в течение которого инвестиции генерируют приток денежных средств. Срок эксплуатации инвестиций в оборудование, как правило, короче физического срока службы этого оборудования.
2. В выборе того или иного проекта на практике не всегда руководствуются критерием “внутренняя ставка рентабельности должна быть выше средневзвешенной стоимости капитала”. Существует целый ряд проектов, осуществление которых диктуется экологической необходимостью или мотивировано повышением безопасности труда. От подобных проектов трудно, да и не следует ожидать значительных чистых денежных потоков. Но тогда доходы от остальных проектов предприятия должны обеспечить такую JRR, чтобы компенсировать пониженные денежные потоки или даже убытки от нерентабельных проектов.

Пример
Предприятие инвестирует 10 млрд. руб., из них 2 млрд. руб. — в необходимые, но нерентабельные проекты. Если средневзвешенная стоимость капитала равна 15%, то 8 млрд. руб. инвестиций должны обеспечить не менее 1,5 млрд. руб. чистых денежных потоков в год (15% на все 10 млрд. руб. инвестиций), т.е. использоваться с рентабельностью не менее 18,75%: