Тема 4. оценка инвестиционных проектов различной продолжительности
В реальной жизни вероятна ситуация, когда необходимо сравнивать проекты различной продолжительности. Рассмотрим следующую ситуацию. Имеется два независимых проекта со следующими характеристиками (млн р.):
А: 100;120;
В: 50;30;40;15.
Требуется ранжировать их по степени приоритетности, если цена капитала 10 %.
Значения NPV при 10 % и IRR для этих проектов соответственно равны:
А: NPV=9,1 млн р. , IRR=20 %;
В: NPV=21,6 млн р., IRR=35,4%.
На первый взгляд можно сделать вывод, что по всем параметрам проект В более предпочтителен. Однако насколько правомочен такой вывод?
Сразу же бросается в глаза временная несопоставимость проектов: первый рассчитан на один год, второй – на три. Поскольку на практике необходимость сравнения проектов различной продолжительности возникает постоянно, разработаны специальные методы, позволяющие элиминировать влияние временного фактора. Это: а) метод цепного повтора; б) метод бесконечного цепного повтора; в) метод эквивалентного аннуитета. Рассмотрим последовательно логику процедур каждого метода.
Метод цепного повтора
Пусть проекты А и В рассчитаны на i и j лет. Для устранения временной несопоставимости рекомендуется:
1) найти наименьшее общее кратное сроков действия проектов НОК = N(ij);
2) рассматривая каждый из проектов как повторяющийся, рассчитать с учетом фактора времени суммарный NPV проектов, реализуемых необходимое число раз в течение периода N;
3) выбрать тот проект из исходных, для которого суммарный NPV повторяющегося потока имеет наибольшее значение.
Суммарный NPV повторяющегося потока равен:
NVP (i,n) = NVP(n) ((1/(1+r)n + (1/(1+r)2n) + ….+ (1/(1+r)N-n + 1)),
где n- число повторений исходного проекта;
i - продолжительность этого проекта;
r – коэффициент дисконтирования в долях единицы.
П р и м е р
Выбрать наиболее предпочтительный проект, если цена капитала 10%:
А: - 100; 50; 70
В: - 100; 30; 40; 60
Таблица 4.1
Чистый дисконтированный доход без учета срока реализации проекта
| Год, t | А | В | Коэффициент дисконтирования r=10% | NPAat | NPAbt |
| -100 | -100 | -100 | -100 | ||
| 0.909 | 45.45 | 27.27 | |||
| 0.751 | 45.06 | ||||
| 0.751 | 45.06 |
NPVA= 3.27 NPVB= 5.37
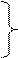nA= 2 года
N= 6 (наименьшее общее кратное)
nB= 3 года
Проект А
1 способ:
Таблица 4.2
| Год, t | Коэффициент дисконтиро- вания r=10% | Денежный поток для 1-й реализации | NVPat | Денежный поток для 2-й реализации | NVPat | Денежный поток для 3-й реализации | NVPat |
| -100 | -100 | ||||||
| 0,909 | 45,45 | ||||||
| 0,826 | 57,82 | -100 | -82,6 | ||||
| 0,751 | NVPa1= 3,27 | 47,81 | -100 | ||||
| 0,683 | 47,81 | -100 | -68,3 | ||||
| 0,621 | NVPa2= 2,76 | 31,05 | |||||
| 0,564 | 39,48 NVPa3= 2,23 |
NVPА= 3.27+2.76+2.23=8.26
2 способ:
Таблица 4.3
| -100 | -30 | -30 | ||||
| 0,909 | 0,826 | 0,751 | 0,683 | 0,621 | 0,564 | |
| -100 | 45,5 | -24,8 | 37,6 | -20,5 | 31,1 | 39,5 |
NVPA = 8.4
3 способ:
NVPА = 3.27* (1+1/(1+0,1)2 + 1/(1+0,1)4) =8,2.
Проект В
NPVB= 5.37*(1+1/(1+0.1)3) = 9.4.
Поскольку суммарный NPV в случае двукратной реализации проекта В больше, следовательно, проект В является предпочтительным.
Метод бесконечного цепного повтора
Рассмотренную в предыдущем вопросе методику можно упростить в вычислительном плане. Так, если анализируется несколько проектов, существенно различающихся по продолжительности реализации, расчеты могут быть достаточно утомительными. Их можно уменьшить, если предположить, что каждый из анализируемых проектов может быть реализован неограниченное число раз. В этом случае при n→∞ число слагаемых в формуле расчета NVP (I,n) будет стремиться к бесконечности, а значение NVP (i, ∞) моджет быть найдено по формуле:
NVP (i, ∞) = lim NVP (i,n) = NVP(i) [(1+r)i/((1+r)I-1)].
n→∞
Из двух сравниваемых проектов проект, имеющий большее значение NVP (i, ∞),является предпочтительным. Так, для рассмотренного примера:
Проект А: i=2;
NVPA (2, ∞) = 3,27 (1+0,1)2/(1+0,1)2-1=18,8 (д.е.).
Проект В, i=3;
NVPВ (3, ∞) = 5,37 (1+0,1)3/(1+0,1)3-1=21,6 (д.е.).
Таким образом, получили те же самые результаты: предпочтительнее проект В, так как NVP по проекту В имеет наибольшее значение.
Метод эквивалентного аннуитета
Этот метод в известной степени корреспондирует с методом бесконечного цепного повтора. Логика и последовательность вычислительных процедур таковы.
1) рассчитать NVP однократной реализации каждого проекта;
2) для каждого проекта находят эквивалентный срочный аннуитет (ЕАА), приведённая стоимость которого равна NVP проекта;
3) рассчитывается бессрочный аннуитет по формуле:
PVa (∞) = EAA/r.
Для приведенного примера:
1) NPVA=3,27;
2) EAA=NPV/FVIFA2.10%= 3.27/1,736=1,88;
3) PVa(∞)=1,88/0,1=18,8 млн р.;
4) NPVB=5,37;
5) EAA=NPV/FVIFA3.10%=5,37/2,487=2,159;
6) PVa(∞)=2,159/0,1=21,6 млн р.
Вновь мы получили тот же самый ответ –предпочтительнее проект В.
Вопросы для самоконтроля
1. Перечислите последовательность действий метода цепного повтора.
2. Охарактеризуйте три способа оценки эффективности проектов различной продолжительности.
3. Какова вычислительная методика бесконечного цепного повтора оценки эффективности проектов различной продолжительности.
4. Какова логика вычислительных процедур метода эквивалентного повтора?
ТЕМА 5. СПЕЦИАЛЬНЫЕ ОБЛАСТИ ПРИМЕНЕНИЯ КРИТЕРИЕВ ОЦЕНКИ ИНВЕСТИЦИОННЫХ ПРОЕКТОВ