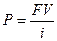А. Простой и сложный процент
ТЕМА 11. КАПИТАЛ И ПРОЦЕНТ
1. Капитал и его образование. Равновесная процентная ставка
2. Элементы финансовой математики
3. Рыночная стоимость капитальных активов
4. Введение в инвестиционный анализ
Капитал и его образование. Равновесная процентная ставка
Капитал – это производственный ресурс, созданный человеком. Различают физический и человеческий капитал. Физический капитал - средства производства - принадлежит фирмам и состоит из основного и оборотного. Основной капитал представляет собой производственные фонды, многократно используемые в процессе производства: здания и сооружения, станки, машины и оборудование, транспортные средства и т.д. Потребление основного капитала есть уменьшение его стоимости вследствие физического и морального износа. Изнашиваясь, основные фонды постепенно переносят свою стоимость на готовую продукцию, что отражается в бухгалтерском учете как амортизационные отчисления.
Оборотный капитал – это производственные фонды, полностью используемые в течение одного производственного цикла: запасы сырья, материалов, полуфабрикатов и т.п.
Человеческий капитал – это принадлежащие людям полезные знания и навыки, используемые в производстве.
Важно отличать капитал как производственный ресурс (капитальные блага) от финансового капитала или денег, вкладываемых в бизнес. Фирмы предъявляют спрос не только на капитальные блага, но прежде всего на временно свободные денежные средства, которые можно потратить на приобретение капитальных благ.
Финансовый капитал возникает тогда, когда домашние хозяйства не расходуют весь свой доход на текущее потребление, но часть его сберегают. Эти сбережения через финансовые рынки попадают к фирмам и используются ими для увеличения капитальных благ, т.е. для инвестиций. Используя капитал, источником которого являются сбережения домашних хозяйств, фирмы платят сберегателям ссудный процент, представляющий собой цену капитала.
Предполагается, что финансовые рынки являются совершенно конкурентными. Иными словами, никто из отдельных сберегателей или фирм не в состоянии повлиять на процентную ставку, изменяя величину предложения своих сбережений либо свой спрос на них. Равновесная рыночная процентная ставка возникает в процессе конкуренции всех сберегателей и инвесторов.
Спрос фирм на финансовый капитал для инвестиций зависит от процентной ставки: чем она ниже, тем больше инвестиции. Поведение сберегателей обычно подчинено обратной логике: чем выше процентная ставка, тем больше сбережения.
Соединим на одном рисунке (рис. 11-1) кривую спроса фирм на денежные средства для инвестиций (DI) и кривую предложения сбережений домашними хозяйствами (SS):
Рис. 11-1. Равновесие на финансовом рынке
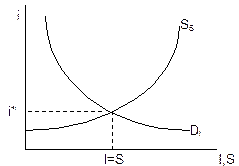
Точка пересечения этих двух кривых дает нам равновесную процентную ставку (i*). При такой ставке финансовые рынки находятся в состоянии равновесия, ибо инвестиции равны сбережениям (I=S).
Отдельная фирма-инвестор не может повлиять на рыночную процентную ставку, но принимает ее как заданную. Поэтому для определения инвестиций, осуществляемых данной фирмой, следует подставить рыночную процентную ставку в функцию инвестиционного спроса фирмы.
Элементы финансовой математики
А. Простой и сложный процент
Пусть некто внес в банк сегодня 100 руб. под 50% годовых. Очевидно, что через год1 на счете будет сумма вклада плюс процент на нее. Последний исчисляется умножением процентной ставки на величину вклада (100*0,5). Итого получаем:
100+0,5*100=100(1+0,5)=150
Решим задачу в общем виде, обозначив начальную сумму вклада - K0, процентную ставку - i и сумму через год - K1. Тогда имеем:
K1=K0+iK0=K0(1+i)
Если начиная со второго года банк начисляет процент только на первоначально вложенную сумму, то такой процент называется простым. В этом случае, вложив 100 руб. под 50% годовых, мы через два года получаем на счете 200 руб. Расчет таков:
100+0,5*100+0,5*100=100(1+2*0,5)=200
Обозначив сумму, которая будет на счете через два года – K2, получаем в общем виде:
K2=K0+iK0+iK0=K0(1+2i). Следовательно, через n лет имеем на счете:
Kn=K0(1+ni)
Если, начиная со второго года, банк начисляет процент на всю накопленную ранее сумму, то такой процент называется сложным. Вернемся к нашему условному примеру с вложением 100 руб. под 50% годовых. Как уже было установлено, мы имеем на счете через год: K1=100(1+0,5)=150. В следующем году процент начисляется уже на 150 руб. Следовательно, через два года на счете будет:
K2=150(1+0,5)=100(1+0,5)(1+0,5)=100(1+0,5)2=225
В общем виде получаем: K2=K0(1+i)2. Таким образом, через n лет сумма на счете (Kn) будет:
Kn=K0(1+i)n
Усложним модель. До этого предполагалось, что деньги вносятся на счет один единственный раз. Теперь допустим, что некто ежегодно вносит в банк одну и ту же сумму (K руб.) под i% годовых (начисляется сложный процент).
В качестве примера предположим, что Вы решили копить деньги к отпуску, для чего первого числа каждого месяца вкладываете в банк K руб. Банк платит по вкладам i% в месяц. Первый взнос сделан 1 сентября, второй – 1 октября и т.д. вплоть до 1 июля, когда Вы больше ничего не вкладываете, а снимаете деньги со счета и уезжаете отдыхать. Итак, подсчитаем:
Первого сентября на счет положено K руб.:
| Дата | Сумма на счете |
| 1 сентября | K |
Первого октября эта сумма превратится в K(1+i), но Вы докладываете еще K руб., и всего на счете оказывается K(1+i)+K руб.:
| Дата | Сумма на счете |
| 1 сентября | K |
| 1 октября | K(1+i)+K |
К первому ноября сентябрьские деньги пролежали на счете два месяца, превратившись в K(1+i)2, октябрьские K руб., будучи на счете один месяц, превратились в K(1+i), кроме того K руб. вносятся дополнительно. Всего, таким образом, Вы имеете на счете K(1+i)2+K(1+i)+K руб.:
| Дата | Сумма на счете |
| 1 сентября | K |
| 1 октября | K(1+i)+K |
| 1 ноября | K(1+i)2+K(1+i)+K |
Декабрь, январь и т.д. пропустим. Наступает 1 июля. К этому времени сентябрьские деньги пробыли на счете 10 месяцев и превратились в K(1+i)10, соответственно деньги, внесенные 1 октября, стали K(1+i)9. И т.д. Последний раз K руб. были вложены 1 июня, т.е. превратились в K(1+i) руб. Поэтому Вы закрываете счет, имея K(1+i)10+K(1+i)9+…+K(1+i) руб.:
| Дата | Сумма на счете |
| 1 сентября | K |
| 1 октября | K(1+i)+K |
| 1 ноября | K(1+i)2+K(1+i)+K |
| … | … |
| 1 июля | K(1+i)10+ K(1+i)9+…+K(1+i) |
Рассмотренный пример – частный случай. Если же подобная операция продолжается n лет (временных периодов), то в конце срока сумма на счете (Kn) будет:
Kn=K(1+i)+K(1+i)2+...+K(1+i)n
Перед нами геометрическая прогрессия, сумма членов которой (Sn) исчисляется по формуле:
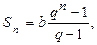
где b - первый член прогрессии [в нашем примере: K(1+i)], q - знаменатель (общий множитель) прогрессии (у нас: 1+i), а n - число членов прогрессии.
Следовательно, в нашем случае:
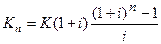
Все приведенные расчеты называются нахождением будущей стоимости (FV). Следовательно: Kn=FVn.
Б. Дисконтирование
Дисконтированием называется исчисление первоначальной суммы денег на основании ее конечной величины. Таким образом, дисконтирование – обратная операция по отношению к нахождению будущей стоимости.
Например, если кто-то хочет иметь на своем счете 150 руб. через год при процентной ставке 50% годовых, то сегодня ему надо вложить в банк 100 руб. Расчет прост:
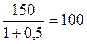
В общем случае вопрос звучит так: какую сумму денег (K0) надо положить сегодня на счет, чтобы через год там было K1 руб., если процентная ставка составляет i% годовых? Ответ:
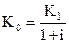
Поставим вопрос в самом общем виде: какую сумму денег надо положить сегодня в банк, чтобы через n лет на счете было Kn руб.? Теперь ответ будет зависеть от того, какой процент начисляет банк: простой или сложный.
Если процент простой, то: 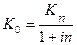
Если процент сложный, то: 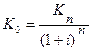
Путем дисконтирования можно определить, какой сумме денег сегодня эквивалентна некоторая сумма, которая будет получена в будущем (FV). Тем самым мы можем рассчитать приведенную стоимостьбудущих денежных поступлений (PV).
Важнейший постулат финансового анализа состоит в том, что деньги имеют различную временную ценность: 100 руб. сегодня предпочтительнее 100 руб., которые будут получены позднее. Это объясняется тем, что сегодняшние деньги индивид уже может как-то использовать, повышая свое благосостояние. Самая простая возможность – положить деньги в банк, и тогда их сумма возрастет.
Пусть банк платит по вкладу 20% годовых. Следовательно, 100 руб. сегодня превратятся в 120 руб. спустя год. Если такие условия устраивают индивида, и он вкладывает деньги, то это означает, что он готов отказаться от 100 руб. сегодня ради 120 руб. через год. Иными словами, 120 руб., получаемых год спустя, для него как минимум равны 100 руб. сегодня. В этом случае результат получается дисконтированием 120 руб. по процентной ставке: 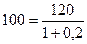
В общем виде, обозначив сумму, получаемую через год – FV1, получаем ее приведенную стоимость:
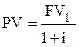
Таким образом, при начислении сложных процентов приведенная стоимость денег, которые будут получены через n лет (FVn), рассчитывается по формуле: 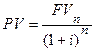
Усложним модель. Предположим, Вы решили сдать квартиру на 5 лет. По договору в конце каждого года арендатор будет платить Вам 3000 долл. Сколько денег Вы получите за все время аренды? Ответ: 15000 долл. по сути не верен, ибо нельзя забывать, что деньги, получение которых растянуто во времени, имеют не одинаковую ценность. В частности, 3000 долл., причитающиеся Вам через год, совсем не равны той же сумме, получаемой через 5 лет. Поэтому просто суммировать или вычитать можно только те деньги, которые пришли или ушли примерно в одно и то же время.
В Вашем случае все будущие доходы надо сначала привести к сегодняшнему дню путем дисконтирования по банковской процентной ставке и только потом их суммировать. В результате будет получена приведенная стоимость всей величины будущих доходов:
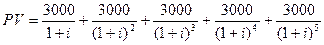
Таким образом, если некто будет ежегодно получать некоторые суммы денег (FVj) руб. в течение n лет, приведенная стоимость всей суммы будущих поступлений составит:
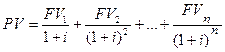
Если доход, получаемый каждый год постоянен (FV), имеем геометрическую прогрессию со знаменателем 1/(1+i):
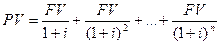
Отсюда:
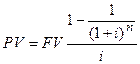
Если число лет бесконечно велико (n®¥), формула упрощается:
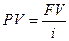
На основе дисконтирования можно решать задачи на погашение займов. Пусть некто взял заем под сложные i% годовых. Выплата в j-ый год составляет FVj. Продисконтировав эту выплату по процентной ставке, находим ее приведенную стоимость:
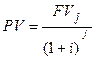
В момент, когда сумма всех дисконтированных выплат становится равна первоначальному долгу, последний считается погашенным.
В качестве примера предположим, что взаймы взяты 100 руб. на 2 года под 100% (i=1) годовых. В первый год заемщик выплатил кредитору 100 руб. В результате погашены только 50 руб. займа, поскольку:
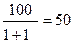
Во второй год выплачено еще 200 руб. Продисконтировав эту сумму, находим:
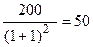
Таким образом, сумма дисконтированных выплат за два года составила величину займа – 100 руб. (50+50=100). Долг погашен.
3.Рыночная стоимость капитальных активов
Капитальный актив – это имущество, приносящее доход. К капитальным активам относятся производственное оборудование, магазин, сдаваемое жилье, участок земли, ценная бумага и т.д. По сути, покупая капитальный актив, люди фактически покупают будущие доходы. Поэтому сегодняшняя цена такого актива будет равна приведенной стоимости этих доходов, определяемой путем дисконтирования.
Следовательно, рыночная стоимость капитального актива (P) зависит от:
- величины приносимых в будущем доходов (FV);
- сроков до получения доходов (n);
- рыночной процентной ставки (i);
- риска неполучения дохода.1
Предположим, капитальный актив – государственная облигация - принесет доход (120 руб.) один единственный раз через год. При этом рыночная процентная ставка составляет 20% годовых. Какую цену согласятся покупатели заплатить за такую облигацию сегодня?
Для ответа на этот вопрос учтем, что у покупателей есть альтернатива: вложить деньги в банк под 20% годовых или в облигацию. Поэтому им не выгодно покупать облигацию дороже, чем за 100 руб. Нет смысла, например, платить 105 руб., чтобы вернуть 120 руб. через год, ибо вложив те же 105 руб. в банк можно через год получить 126 руб. Разумеется, ни один из покупателей не отказался бы от покупки облигации дешевле, чем за 100 руб. Покупка, например, за 90 руб. является в их глазах выгодной сделкой: платим сегодня 90 руб., через год получаем 120 руб., если же вложить эти 90 руб. в банк, то больше 108 руб. получить не удастся.
К огорчению покупателей такой вариант вряд ли пройдет. Даже если некоторые из нынешних владельцев облигаций, остро нуждаясь в деньгах, и согласятся уступить их за бесценок, в условиях конкурентного рынка набежит столько желающих приобрести облигации, что их цена автоматически возрастет. В конечном счете цена данной облигации будет колебаться вокруг 100 руб.:
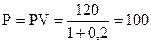
При такой цене покупателям становится безразлично, куда вкладывать деньги – в банк или в облигацию.
В общем случае сегодняшняя рыночная цена капитального актива, который принесет доход один раз через один год, определяется по формуле:
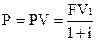
Именно такую сумму и согласится инвестор заплатить сегодня за данный актив.
Соответственно, если актив принесет доход (FVn) первый и единственный раз только через n лет, цена актива сегодня составит:
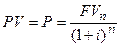
Если актив приносит доход каждый год на протяжении n лет, формула принимает вид:
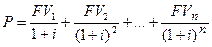
Если доход, получаемый каждый год постоянен (FV1=FV2=…=FVn=FV), а число лет бесконечно велико, формула упрощается: