Эквивалентность сложных процентных ставок
| Сложная процентная ставка (iсл) | Сложная учетная ставка (dсл) | |
| Сложная учетная ставка (dсл) | 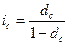 (21) (21) 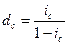 (22) (22) | |
| Сложная номинальная процентная ставка (j) при начислении процентов m раз в год | 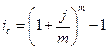 (23) (23) 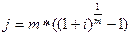 (24) (24) | 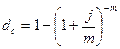 (25) (25) 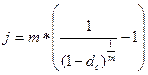 (26) (26) |
Внимание! Полученная по формуле (23) годовая ставка сложных процентов, эквивалентная номинальной процентной ставке, называется эффективной ставкой сложных процентов.
Эффективная ставка измеряет тот реальный относительный доход, который получает кредитор в целом за год. Иначе говоря, она отвечает на вопрос: какую годовую ставку сложных процентов необходимо установить, чтобы получить такой же финансовый результат, как при m – разовом начислении процентов год по ставке 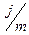 . Эффективную ставку сложных процентов полезно знать, чтобы оценить реальную доходность финансовой операции, или сравнивать процентные ставки в случае, когда используются различные интервалы начисления. Очевидно, что значение эффективной ставки больше значения номинальной, а совпадают они при m=1.
. Эффективную ставку сложных процентов полезно знать, чтобы оценить реальную доходность финансовой операции, или сравнивать процентные ставки в случае, когда используются различные интервалы начисления. Очевидно, что значение эффективной ставки больше значения номинальной, а совпадают они при m=1.
Задача 8. Можно ли с помощью двух различных ставок получить один и тот же финансовый результат? Поясните на примере.
__
__
Задача 9. Определите номинальную ставку сложных процентов при их ежеквартальном начислении, эквивалентную сложной учетной ставке dc =15% годовых.
Решение:
Проверка:
Задача 10. Определите эффективную ставку сложных процентов с тем, чтобы получить такую же наращенную сумму, как и при использовании номинальной ставки j = 18%, при ежеквартальном начислении процентов.
Решение:
Проверим данный расчет. Предположим, что выдан кредит в размере 400 тыс. руб. по ставке _______ (сложные проценты) на срок два года. Наращенная сумма долга составит:
FV =
FV =
Задача 11. Срок уплаты по долговому обязательству – полгода, простая учетная ставка равна 18 %. Какова доходность данной операции, измеренная в виде простой ставки ссудного процента?
Решение:
Задача 12. Рассчитать Эффективную ставку сложных процентов, если номинальная ставка равна 24 % и начисление процентов происходит ежемесячно.
Решение:
Задача 13. Определить, под какую ставку процентов выгоднее поместить капитал в 10 000 000 руб. на пять лет:
а) под простую
б) под сложную ставку в 25 % при ежеквартальном начислении?
Решение: В данном случае не обязательно считать величину наращенной суммы, получаемой при различных ставках. Поэтому не важна величина первоначального капитала. Достаточно найти, например, простую процентную ставку, эквивалентную данной сложной процентной ставке:
Так как простая процентная ставка, которая дала бы одинаковый с данной сложной процентной ставкой результат значительно превышающий предложенный (30%), ясно, что гораздо выгоднее использовать сложную процентную ставку. Подсчитаем теперь наращенные суммы, получаемые в обоих случаях, чтобы выяснить насколько более выгодна сложная ставка. Используем для этого формулы (1) и (20)
FV =
FV =
Задача 14. Определить номинальную ставку процентов, которая обеспечивала бы годовую доходность в 26 %, если начисление процентов происходит ежемесячно по сложной процентной ставке.
Решение:
Определение эквивалентности, при несовпадении начальных условий. Можно определить также процентную ставку, эквивалентную данной, когда начальные условия полностью или частично не совпадают. Данная ситуация может возникнуть, например, если есть возможность выбора между различными коммерческими предложениями.
Рассмотрим следующую задачу:
Какова должна быть сложная учетная ставка dc чтобы сумма РV1, вложенная под эту ставку на n1 лет, достигла той же величины, что и сумма РV2, вложенная под сложную ставку ссудного процента iс на n2 лет?
Поскольку финансовые результаты обеих операций должны быть равны, составляем следующее уравнение эквивалентности:
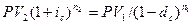 | (27) |
Отсюда
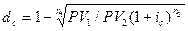 | (28) |
Можно решить уравнение относительно iс, тогда
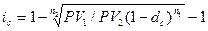 | (29) |
Как определить, что выгоднее, заплатить сумму FV1 через n1 лет или сумму FV2 через n2 лет? Будем считать, что FV1 < FV2 и n1 < n2 (иначе задача имеет тривиальное решение).
В зависимости от размера процентной ставки (возьмем для примера сложную ставку ссудного процента), под которую могут быть вложены деньги, суммы FV1 и FV2 имеют различные современные величины PV1 и РV2:
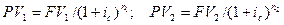 | (30) |
В этом случае выгоднее выплачивать меньшую сумму FV1. Поскольку n1< n2, для достаточно больших ic будет выполняться PV1> РV2. Тогда найдется i0, уравнивающая ставка, при которой современные величины обеих сумм совпадут.
Т.е.
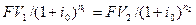 |
Откуда
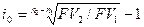 | (31) |
ü Для всех ic < i0 предпочтительнее вариант с меньшей суммой и меньшим сроком.
ü Для ic > i0 - с большими.
ü При iс= i0 финансовые результаты обеих операций эквивалентны.
Аналогичные формулы могут быть получены для всех видов процентных ставок.
Задача 15. Капитал, взятый в кредит, вложен под сложную ставку ссудного процента 22% годовых. Для расчета с кредиторами необходимо выплатить 30 000 000 через два года или 36 000 000 через три года. Какой вариант предпочтительней?
Решение: По формуле (31) найдем уравнивающую процентную ставку:
