Определение внутренней нормы доходности инвестиций

Под внутренней нормой прибыли инвестиции (RR-синонимы: внутренняя доходность, внутренняя окупаемость) понимают значения коэффициента дисконтирования r, при котором NPV проекта равен нулю:

IRR=r, при котором NPV=f(r)=0.

Иными словами, если обозначить IC=CF₀, то IRR находится из уравнения:

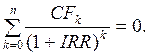(5.7)

Для наиболее наглядного понимания природы критерия IRR воспользуемся графическим методом. Рассмотрим функцию:

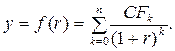(5.8)

Эта функция обладает рядом примечательных свойств: некоторые из них носят абсолютный характер, т.е. не зависят от вида денежного потока, другие проявляются лишь в определенных ситуациях, т.е. характерны специфическим потокам. Во-первых, из вида зависимости видно, что y=f(r) – нелинейная функция; как будет показано ниже, это свойство может иметь очень серьезные последствия при расчете критерия IRR.

Во-вторых, очевидно, что при r=0 выражение в правой части (5.8) преобразуется в сумму элементов исходного денежного потока, иными словами, график NPV пересекает ось ординат в точке, равной сумме всех элементов недисконтированного денежного потока, включая величину исходных инвестиций.

В-третьих, из формулы (5.8) видно, что для проекта, денежный поток которого с позиции логики инвестирования и с определенной долей условности можно назвать классическим в том смысле, что отток (инвестиция) сменяется притоками, в сумме превосходящими этот отток, соответствующая функция y=f(r) является убывающей, т.е. с ростом r график функции стремится к оси абсцисс и пересекает ее в некоторой точке, как раз и являющейся IRR (рис. 5.3).

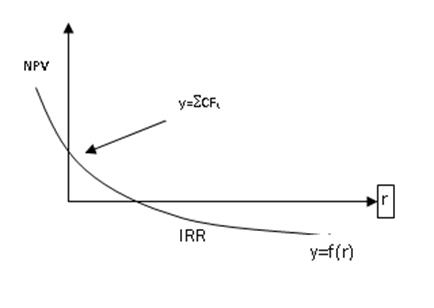
Рис. 5.3 - График NPV классического инвестиционного проекта

В-четвертых, ввиду нелинейности функции y=f(r), а также возможных в принципе различных комбинаций знаков элементов денежного потока, функция может иметь несколько точек пересечения с осью абсцисс.

В-пятых, вновь благодаря тому, что y=f(r) нелинейна, критерий IRR не обладает свойством аддитивности.

В дальнейшем при рассмотрении примеров мы будем неоднократно сталкиваться с ситуациями, иллюстрирующими сформулированные свойства критерия IRR.

Смысл расчета внутренней нормы прибыли при анализе эффективности планируемых инвестиций, как правило, заключается в следующем: IRR показывает ожидаемую доходность проекта, и, следовательно, максимально допустимый относительный уровень расходов, которые могут быть ассоциированы с данным проектом (данное утверждение верно лишь для «классического» проекта том смысле, в каком он был определен ранее в данном разделе). Например, если проект полностью финансируется за счет коммерческого банка, то значение IRR показывает верхнюю границу допустимого уровня банковской процентной ставки, превышение которого делает проект убыточным.

На практике любая коммерческая организация финансирует свою деятельность, в том числе и инвестиционную, из различных источников. В качестве платы за пользование авансированными в деятельность организации финансовыми ресурсами она уплачивает проценты, дивиденды, вознаграждения и т.п., иными словами, несет некоторые обоснованные расходы на поддержание экономического потенциала. Показатель, характеризующий относительный уровень этих расходов в отношении долгосрочных источников средств, как обсуждалось выше, называется средневзвешенной ценой капитала (WACC). Этот показатель отражает сложившийся в коммерческой организации минимум возврата на вложенный в ее деятельность капитал, его рентабельность и рассчитывается по формуле средней арифметической взвешенной.

Таким образом, экономический смысл критерия IRR заключается в следующем: коммерческая организация может принимать любые решения инвестиционного характера, уровень рентабельности которых не ниже текущего значения показателя «цена капитала» CC, под последним понимается либо WACC, если источник средств точно не идентифицирован, либо цена целевого источника, если таковой имеется.

Именно с показателем CC сравнивается критерий IRR, рассчитанный для конкретного проекта, при этом связь между ними такова. Если IRR > CC, то проект следует принять; IRR < CC, то проект следуетотвергнуть; IRR = CC, то проект не является ни убыточным, ни прибыльным.

Независимо от того, с чем сравнивается IRR, очевидно одно: проект принимается, если его IRR больше некоторой пороговой величины, поэтому при прочих равных условиях, как правило, большее значение IRR считается предпочтительным.

Практическое применение данного метода осложнено, если в распоряжении аналитика нет специализированного финансового калькулятора. В этом случае применяется метод последовательных итераций с использованием табулированных значений дисконтирующих множителей. Для этого с помощью таблиц выбираются два значения коэффициента дисконтирования r₁<r₂ таким образом, чтобы в интервале (r₁,r₂) функция NPV=f(r) меняла свое значение с «+» на «-» или с «-» на «+». Далее применяют формулу:

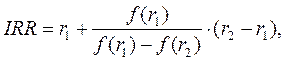(5.9)

где r₁ – значение табулированного коэффициента дисконтирования, при котором f(r₁)>0 (f(r₁<0); r₂ – значение табулированного коэффициента дисконтирования, при котором f(r₂)<0 (f(r₂>0).

Точность вычислений обратно пропорциональна длине интервала (r₁,r₂), а наилучшая аппроксимация табулированных значений достигается в случае, когда длина интервала минимальна (равна 1%), т.е. r₁ и r₂ – ближайшие друг к другу значения коэффициента дисконтирования, удовлетворяющие условиям (в случае изменения знака функции y=f(r) с «+» на «-»):

r₁ – значение табулированного коэффициента дисконтирования, минимизирующее положительное значение показателя NPV, т.е. ;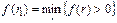

r₂ – значение табулированного коэффициента дисконтирования, максимизирующее отрицательное значение показателя NPV, т.е. .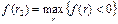

Путем взаимной замены коэффициентов r₁ и r₂ аналогичные условия выписываются для ситуации, когда функция меняет знак с «-» на «+».

Пример. Требуется рассчитать значения показателя IRR для проекта, рассчитанного на три года, требующего инвестиций в размере 10 млн. руб. и имеющего предполагаемые денежные поступления в размере 3 млн. руб., 4 млн. руб., 7 млн. руб.

Возьмем два произвольных значения коэффициента дисконтирования: r₁=10% и r₂=20%. Соответствующие расчетыс использованием табулированных значений приведены в табл. 5.3. Тогда значение IRR вычисляется следующим образом:

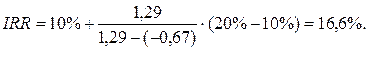Можно уточнить полученное значение. Допустим, что путем нескольких итераций мы определили ближайшие целые значения коэффициента дисконтирования, при которых NPV меняет знак: при r=16% – NPV=+0,05; при r=17% – NPV=-0,14.

Тогда уточненное значение IRR будет равно:

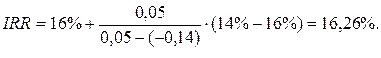Истинное значение показателя IRR равно 16,23%, т.е. метод последовательных итераций обеспечивает весьма высокую точность (отметим, что с практической точки зрения такая точность является излишней). Свод всех вычислений приведен в таблице 5.3.

Таблица 5.3 - Исходные данные для расчета показателя IRR

Год	По- ток	Расчет 1	Расчет 2	Расчет 3	Расчет 4
r=10%	PV	r=20%	RV	r=16%	PV	r=17%	PV
0-й	-10	1,000	-10,00	1,000	-10,00	1,000	-10,00	1,000	-10,00
1-й		0,909	2,73	0,833	2,50	0,862	2,59	0,855	2,57
2-й		0,826	3,30	0,694	2,78	0,743	2,97	0,731	2,92
3-й		0.751	5,26	0,579	4,05	0,641	4,49	0,624	4,37
			1,29		-0,67		0,05		-0,14

Рассмотренная методика применима лишь к акционерным обществам. В организациях, не являющихся акционерными, некоторым аналогом показателя WACC является уровень издержек производства и обращения (дебетовый оборот счета 46 «Реализация») в процентах к общей сумме авансового капитала (итог баланса-нетто).