Сложные учетные ставки

Рассмотрим антисипативный способ начисления сложных процентов.

Пусть

dс(%) – сложная годовая учетная ставка;

dc − относительная величина сложной учетной ставки;

kн.у − коэффициент наращения для случая учетной ставки;

f − номинальная годовая учетная ставка.

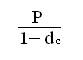Тогда по прошествии первого года наращенная сумма S в соответствии с формулой (2.5) состоит

S1 = .

Еще через год эта формула будет применяться уже к сумме S :

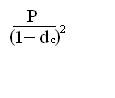
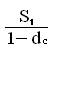
S2 = =

и т.д., аналогично случаю сложных ставок ссудных процентов.

По отношению n лет наращенная сумма состоит

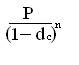
S = (4.1)

Отсюда для множителя наращения имеем

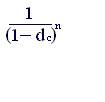
kн.у = (4.2)

Сравнивая формулы (3.1) и (4.1), легко видеть, что при равенстве ссудного процента и учетной ставки наращение первоначальной суммы во втором случае (антисипативный метод) идет быстрее.

Для небольших процентных ставок декурсивный метод начислении более выгоден для заемщика, а антисипативный – для кредитора (см. рис.2 в приложении). Но с ростом процентной ставки разница в величине наращенной суммы становится огромной (при этом она сама растет с ростом n), и сравнение двух методов с точки зрения выгодности утрачивает смысл. Представить себе эту разницу можно с помощью графика на рис.3 (смотри приложение).

Из формулы (4.1) следует, что для периодов начисления, превышающих один год, учетная ставка может принимать значения только строго меньшие (т.е. не достигающие) 100%.

Так же, как и при декурсивном способе, возможны различные варианты начисления антисипативных процентов (начисление за короткий – меньше года – интервал, начисление m раз в году и т.д.). Им будут соответствовать формулы, полученные аналогичным образом.

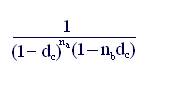Так, для периода начисления, не являющегося целым числом, имеем

kн.у = (4.3)

При учетной ставке, изменяющейся в течение срока ссуды, наращенная сумма превращается в

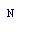
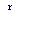
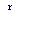
S = P / ∏ (1-n d ) (4.4)

Здесь n1, n2, …, nN - продолжительность интервалов начисления в годах, d1, d2 , …, dN- учетные ставки, соответствующие данным интервалам.

Для начисления процентов m раз в году формула имеет такой вид:

S = P/ (1- f/m ) (4.5)

или

S = P/ [(1− f/m) (1−l∙ f/m)] (4.6)

При этом mn – целое число интервалов начисления за весь период начисления, l – часть интервала начисления.

При непрерывном начислении процентов S рассчитывается по формуле:

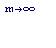S = P / lim (1 – f/m) (4.7)

Из полученных формул путем преобразований получаем формулы для нахождения первоначальной суммы, срока начисления и величины учетной ставки:

P = S (1 – dc) ; (4.8)

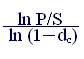
n = ; (4.9)

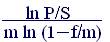
n = ; (4.10)

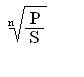
dс = 1 − ; (4.11)

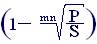
f = m . (4.12)

Таким образом, мы рассмотрели различные способы начисления процентов. В приложении дана таблица (таблица №1), которая наглядно показывает результаты, получаемые при этих способах для одной и той же первоначальной суммы, одинаковых по величине процентных ставок и периодов начисления n.

Рассмотрим примеры.

ПРИМЕР 13

Первоначальная сумма долга равняется 25 000 000 руб. Определить величину наращенной суммы через три года при применении декурсивного и антисипативного способов начисления процентов. Годовая ставка – 25%.

Решение:

По формулам (3.1) и (4.1) получаем:

S = 25 000 000∙(1+0,25) = 48 828 125 (руб.)

S = 25 000 000/(1-0.25) = 59 255 747 (руб.).

Данный пример наглядно демонстрирует ощутимость различия в результатах при разных способах начисления процентов. Разница составляет больше 10 млн. руб.

ПРИМЕР 14

Определить современное значение суммы в 120 000 000 руб., которая будет выплачена через два года, при использовании сложной учетной ставки 20% годовых.

Решение:

По формуле (4.8):

P = 120 000 000∙(1-0,2)² = 76 800 000 (руб.).