Примеры для закрепления материала темы «Финансово-математические основы инвестиционного проектирования»

2.1. Предположим Вы купили шестилетний 8-ми процентный сберегательный сертификат стоимостью 1000 рублей. Если проценты начисляются ежегодно, какую сумму Вы получите по окончанию контракта?

Решение.

Используем формулу наращения денег, т.е. определяем будущую стоимость 1000 рублей через 6 лет при 8 процентах годовой прибыли:

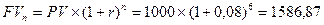руб.

2.2. Финансовый менеджер предприятия предложил Вам инвестировать Ваши 5000 руб. в его предприятие, пообещав возвратить Вам 6000 через два года. Имея другие инвестиционные возможности, Вы должны выяснить, какова процентная ставка прибыльности предложенного Вам варианта.

Решение.

Используем основную формулу наращения денег:

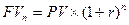
откуда следует

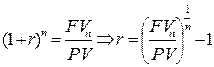
В нашем случае

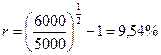
Ясно, что если кто-либо предложит Вам инвестировать Ваши деньги под, хотя бы, 10 процентов годовых, Вы отклоните предложение получить 6000 руб. через два года, вложив сейчас 5000 рублей.

2.3. Вам предлагают инвестировать деньги с гарантией удвоить их количество через пять лет. Какова процентная ставка прибыльности такой инвестиции?

Решение.

Используем основную формулу предыдущей задачи, учитывая, что будущее значение какой-либо суммы через пять лет FV₅ и ее современное значение PV относятся как 2:1.

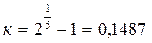
то есть 14,87 процентов.

2.4.Предприятие собирается приобрести через три года новый станок стоимостью 8000000. Какую сумму денег необходимо вложить сейчас, чтобы через три года иметь возможность совершить покупку, если процентная ставка прибыльности вложения составляет

а) 10 процентов?

б) 14 процентов?

Решение.

По условию задачи мы должны определить современное значение стоимости станка 8000000 при ставке дисконта 10 процентов. Используем формулу дисконтирования:

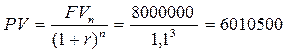руб.

Аналогично рассчитаем для случая б):

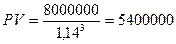руб.

Закономерно, что во втором случае сумма вклада получилась меньше.

2.5. Проведя усовершенствование технологического процесса предприятие в течение пяти последующих лет планирует получение ежегодное увеличение денежного дохода на 10.000000 рублей. Эти деньги оно собирается немедленно вкладывать под 10 процентов годовых, желая через пять лет накопить сумму для приобретения нового оборудования. Какую сумму денег предприятие получит через пять лет?

Решение.

По условию задачи предприятие планирует получить аннуитет 10.000000 руб. в течение пяти лет. Для определения суммы накопленных денег необходимо вычислить будущее значение пятилетнего аннуитета при процентной ставке наращения 10 процентов. Используем формулу будущего значения аннуитета:

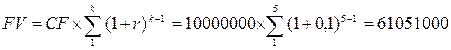руб.

2.6.Предприятие располагает 160000 рублей и предполагает вложить их в собственное производство, получая в течение четырех последующих лет ежегодно по 50000 руб.. В то же время предприятие может купить на эту сумму акции одной солидной корпорации, приносящие 12 процентов годовых. Какой вариант Вам представляется более приемлемым, если считать что более выгодной возможностью вложения денег (чем под 12 процентов годовых) предприятие не располагает?

Решение.

Для ответа на вопрос можно воспользоваться двумя способами рассуждения. Сравним будущее наращенное значение аннуитета 50000 руб. при процентной ставке 12 процентов с будущим значением альтернативного вложения всей суммы 160000 руб. при той же процентной ставке:

будущее значение аннуитета –

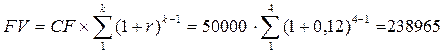руб.

будущее значение 160000 рублей –

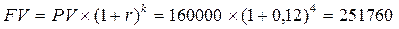руб.

Результаты расчетов говорят о том, что покупка акций более выгодна, чем вложение этой же суммы денег в собственное производство.

Возможен другой подход к решению задачи, использующий приведение денежных потоков к настоящему времени. Этот подход более распространен в практике, поскольку он проще. В данном случае мы просто определяем настоящее значение аннуитета 50000 руб. при показателе дисконтирования 12 процентов:

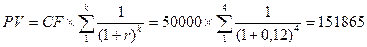руб.

Сравнивая полученное значение с суммой имеющихся в настоящее время денежных средств 160000, приходим к такому же выводу: вкладывать деньги в акции солидной компании более выгодно.

Можно заметить, что численное значение различия альтернативных вариантов вложения в настоящее время 160000 - 151865 = 8135 руб. существенно меньше численного различия через четыре года 251760 -238965 = 12795 руб. Это закономерно ввиду феномена стоимости денег во времени: если мы дисконтируем 12795 на четыре года при показателе дисконта 12% (12795×0,636 (из приложения 2)), то получим 8137,6 руб. Отсутствие абсолютного совпадения объясняется только погрешностью расчетов, связанной округлением денежных сумм до целых значений.

2.7.Предприятие рассматривает два альтернативных проекта капитальных вложений приводящих к одинаковому суммарному результату в отношении будущих денежных доходов (руб.) :

Год	Проект 1	Проект 2
Всего

Оба проекта имеют одинаковый объем инвестиций. Предприятие планирует инвестировать полученные денежные доходы под 18 процентов годовых. Сравните современные значения полученных денежных доходов.

Решение.

Вычислим современные значения последовательностей денежных доходов по каждому проекту, дисконтируя ежегодные доходы при показателе дисконта 18%. Расчеты проведем с помощью специальных таблиц.

Проект 1

Год	Денежный поток (руб.)	Множитель дисконта (из приложения 2)	Современное значение (руб.)
			4 = 2×3
		0.8475	2542.50
		0.7182	2872.80
		0.6086	3043.00
		0.5158	3094.80
Суммарное современное значение	11553.10

Проект 2

Год	Денежный поток (руб.)	Множитель дисконта (из приложения 2)	Современное значение (руб.)
			4 = 2×3
		0.8475	5085.00
		0.7182	2872.80
		0.6086	3043.00
		0.5158	1547.40
Суммарное современное значение	12548.20

По результатам расчетов можно сделать вывод о предпочтительности второго проекта.