Наращение, дисконтирование и банковский учет по сложным ставкам
Наращение и дисконтирование по простым процентным ставкам
В практических финансовых операциях суммы денег всегда связываются с конкретными моментами и периодами времени. Фактор времени играет наиболее важную роль, поэтому необходимость его учета выражается в принципе неравноценности денег, относящихся к разным моментам времени.
Процентные деньги или проценты - абсолютная величина дохода от предоставления денег в долг в любой его форме.
Период начисления (n) - временной интервал, к которому приурочена процентная ставка.
Процентная ставка - отношение дохода (процентных денег) к сумме долга за единицу времени:
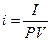 ,
,
где i – процентная ставка;
PV – первоначальная сумма ссуды;
I – сумма перечисленных процентов.
Наращенная сумма ссуды, долга, депозита (FV) - первоначальная ее сумму с начисленными процентами к концу срока:
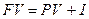
Если ставки процентов применяются к одной и той же начальной сумме на протяжении всего срока ссуды – это простые процентные ставки.
Основная формула наращения денег по простым процентным ставкам имеет вид:
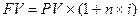 ,
,
где 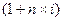 - множитель наращения простых процентов. Отсюда:
- множитель наращения простых процентов. Отсюда:
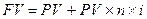
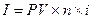
Банковский учет по простой учетной ставке
Процесс начисления процентов и их удержания называют учетом.
Суть операции учета: банк до наступления срока платежа по векселю или иному платежному обязательству приобретает его у владельца по цене, которая меньше суммы, указанной на векселе, т.к. покупает (учитывает) его с дисконтом (т.е. со скидкой). Получив при наступлении срока векселя деньги, банк реализует дисконт.
При банковском учете применяется простая или сложная учетная ставка d:
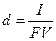 .
.
Формула банковского учета по простой учетной ставке:
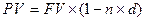 ,
,
где n – срок от момента учета до даты погашения векселя.
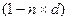 - дисконтный множитель по простой учетной ставке.
- дисконтный множитель по простой учетной ставке.
Важно! При учете векселя временная база – 360 дней.
Операции начисления процентов и дисконтирования по учетной ставке могут совмещаться. Например, при учете долгового обязательства, предусматривающего начисление простых процентов, следует решить две задачи:
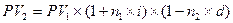 ,
,
где 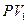 - первоначальная сумма ссуды;
- первоначальная сумма ссуды;
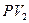 - сумма, полученная при учете;
- сумма, полученная при учете;
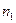 - общий срок платежного обязательства (срок начисления процентов);
- общий срок платежного обязательства (срок начисления процентов);
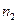 - срок от момента учета до даты погашения долгового обязательства, причем
- срок от момента учета до даты погашения долгового обязательства, причем 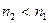 .
.
Наращение, дисконтирование и банковский учет по сложным ставкам
Если проценты не выплачиваются сразу после начисления, а присоединяются к сумме долга, то для наращения применяются сложные проценты. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называют капитализацией процентов. Формула для расчета наращенной суммы при ежегодной капитализации процентов имеет вид:
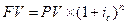 ,
,
где 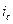 - годовая сложная ставка процентов;
- годовая сложная ставка процентов;
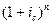 - множитель наращения по сложной процентной ставке.
- множитель наращения по сложной процентной ставке.
Кроме этого существует смешанный метод начисления процентов, который предполагает начисление процентов за целое число лет по формуле сложных процентов и по формуле простых процентов – за дробную часть периода:
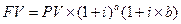 ,
,
где а – целое число периодов (лет);
b – дробная часть периода, т.е. n = a + b.
На практике наращение денег производится один раз в году по ставке i или m раз в году по ставке j/m.
Годовая ставка i, при которой финансовый результат не будет отличаться от результата при начислении процентов m раз в году по ставке j/m, называется эффективной или действительной ставкой; j при этом является номинальной ставкой.
Эффективная ставка характеризует тот реальный относительный доход, который получает кредитор за год при начислении процентов m раз в году по ставке j/m. Расчет наращенной суммы с использованием номинальной процентной ставки при m-разовом начислении процентов в году производится по формуле:
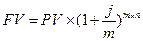 ,
,
где m – количество начислений процентов в году.
По определению:
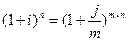 отсюда:
отсюда: 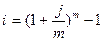 .
.
Замена в договоре номинальной ставки j при m-разовом начислении процентов на эффективную ставку i не изменяет финансовых обязательств сторон, т.е. обе ставки эквивалентны в финансовом отношении.
Формула математического дисконтирования по сложной процентной ставке:
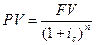 ,
,
где 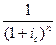 - дисконтный множитель по сложной процентной ставке.
- дисконтный множитель по сложной процентной ставке.
При наращении и капитализации процентов m раз в году:
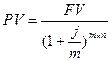 ,
,
где 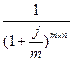 - дисконтный множитель.
- дисконтный множитель.
Формула банковского учета по сложной учетной ставке:
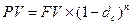 ,
,
где 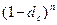 - дисконтный множитель по сложной учетной ставке.
- дисконтный множитель по сложной учетной ставке.
Дисконтирование может производиться не один, а m раз в году, т.е. каждый раз учет производится по ставке f/m. В этом случае:
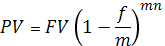 ,
,
где f – номинальная годовая учетная ставка.
Эффективная учетная ставка (d) характеризует степень дисконтирования за год. Определим ее на основе равенства дисконтных множителей:
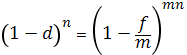 ,
,
откуда
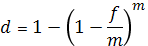 .
.
В свою очередь
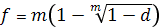 .
.
