Дивиденды и проценты по ценным бумагам

ДОХОДНОСТЬ ОПЕРАЦИЙ С ЦЕННЫМИ БУМАГАМИ

Вложения денежного капитала в различного вида ценные бумаги (долевое участие в предприятиях, займы другим предприятиям под векселя или иные долговые обязательства) – важнейший элемент развивающейся рыночной экономики. Цель финансовых вложений – получение дохода и/или сохранение капитала от обесценивания в условиях инфляции. Следовательно необходимо уметь правильно оценивать реальный доход по разного ценным бумагам . Рассмотрим сначала виды существующих в настоящее время ценных бумаг и определим разницу в начислении процентов и возможностей получения дохода по ним.

В зависимости от формы предоставления капитала и способа выплаты дохода ценные бумаги делятся на долговые и долевые.

Долговые ценные бумаги (купонные облигации, сертификаты, векселя) обычно имеют фиксированную процентную ставку являются обязательством выплатить полную сумму долга с процентами на определенную дату в будущем; по дисконтным облигациям доход представляет собой скидку с номинала.

Долевые ценные бумаги (акции) представляют собой непосредственную дол. Держателя в реальной собственности и обеспечивают получение дивиденда в неограниченное время.

Все прочие виды ценных бумаг являются производными от долговых либо долевых ценных бумаг и закрепляют право владельца на покупку или продажу акции и долговых обязательств. Это опционы, фьючерсные контракты, приватизационные чеки.

Расчет дохода по различным видам ценных бумаг производится на основе полученных в предыдущих параграфах формул. Приведем несколько примеров.

ПРИМЕР 29

Депозитный сертификат номиналом 200 000 руб. выдан 14 мая с погашением 8 декабря под 18% годовых. Определить сумму дохода при начислении точных и обыкновенных процентов и сумму погашения долгового обязательства.

Решение

Находим сначала точное (17 дней мая + 30 дней июня + 31 день июля + 31 день августа + 30 дней сентября + 31 день октября + 30 дней ноября + 30· · 6 + 8 дней декабря = 205 дней) число дней займы.

Для точных процентов из формул (1.2) и (1.3) получаем

I = 0,18 · 200 000 · 208/365 = 20 515 (руб.)

По формуле (1.4) вычисляем сумму погашения обязательства:

S = 200 000 + 20 515 = 202 515 (руб.)

Для случая обыкновенных процентов возможно несколько способов расчета:

а) ∂ = 208, К = 360. Тогда

I = 0,18 · 200 000 · 208/360 = 20 800 (руб.)

S = 200 000 + 20 800 + 220 800 (руб.).

б) ∂ = 205, К = 365. Тогда

I = 0,18 · 200 000 · 205/365 = 20 219 (руб.)

S = 200 000 + 20 219 = 220 219 (руб.)

в) ∂ = 205, K = 360. Тогда

I = 0,18 · 200 000 · 205/360 = 20 500 (руб.)

S = 200 000 + 20 500 = 220 500 (руб.)

ПРИМЕР 30

Вексель выдан на сумму 10 000 000 руб. со сроком оплаты 21 июля. Владелец векселя учел его в банке 5 июля по учетной ставке 20%. Определить доход банка и сумму, полученную по векселю (К = 365).

Решение

Срок от даты погашения составляет 21 – 5 = 16 дней. По формуле (2.3) получаем

D = 0.2 · 10 000 000 · 16/365 = 87 671 (руб.)

Соответственно, по формуле (2.4), сумма, полученная по векселю:

P = 10 000 000 – 87 671 = 9 912 329 (руб.)

При операциях с облигациями источником дохода являются фиксированные проценты (в случае купонных облигаций), а также разность между ценой, по которой облигации приобретается, и ценой, по которой она выкупается. Выкупная цена облигации обычно совпадает с ее номиналом.

Существуют облигации без выплаты процентов (дисконтные облигации), инвестированные средства в которые будет доходным только при покупке их со скидкой с номинала, т.е. с дисконтом.

Введем обозначения:

N – номинальная стоимость облигации;

P0 – цена покупки облигации;

I0 – доход по облигации;

n – период. За который начисляются проценты;

i – процентная ставка;

ic – эффективная ставка сложных процентов.

При расчетах дохода используют понятие курса облигации Pk:

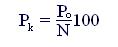
(8.1)

Тогда

Io = N (1 + i)ⁿ. (8.2)

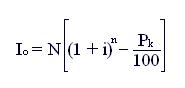Подставляя в эту формулу выражение (8.1), получим

(8.3)

Если для измерения доходности использовать эффективную ставку сложных процентов, следует применять формулу (3.1):

Io = Po (1 + ic)ⁿ – Po.

ПРИМЕР 31

Рассчитать доходность покупки облигации в виде эффективной ставки сложных процентов, если облигация номиналом 10 000 руб., выпущенная на пять лет, приобретена по курсу 120, и на нее начисляется ежегодно сложные проценты по ставке 18%.

Решение

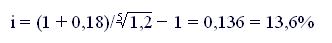Используем формулу (8.4):

При покупке акции источником дохода могут быть дивиденды и разница между ценой приобретения и ценой продажи.

Фиксированные дивиденды (определенный процент от номинальной стоимости акции) выплачиваются по привилегированным акциям.

Введем обозначения:

Pa – цена приобретения акции;

Q – цена продажи акции;

N – номинальная цена акции;

F – величина дивидендов;

IF – доход от дивидендов;

Ia – общий доход от покупки акции;

n – срок в годах от момента покупки до момента продажи.

Тогда

Ia = IF + Q – Pa. (8.5)

Если дивиденды вновь не реинвестируются, доход от них будет равен

IF = n F N. (8.6)

Величина дивидендов по простым акциям устанавливается общим собранием акционеров в зависимости от финансовых результатов года (дивиденды могут и не выплачиваться, если прибыли нет или она целиком направляется на развитие), поэтому расчет дохода от таких акций может быть только ориентировочным и производится по выражениям (8.5) и (8.6).

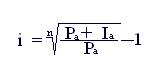Формула для расчета доходности покупки акции в виде эффективной ставки сложных процентов:

(8.7)

ПРИМЕР 32

При выпуске акции номиналом в 5 000 руб. объявленная величина дивидендов равна 15% годовых, а их стоимость, по оценкам, будет ежегодно возрастать на 4% по отношению к номиналу. Определить ожидаемый доход от покупки по номиналу и последующей продажи через пять лет 100 таких акций.

Решение

Величина годовых дивидендов от 100 акций равняется

IF = 100 · 0,15 · 5 000 = 75 000 ( руб.)

Стоимость 100 акций через пять лет:

Q100 = 100 (5 000 + 5 · 0,04 · 5 000) = 600 000 (руб.)

Общий доход, рассчитанный по формуле (8.5), составит

Ia = 75 000 + 600 000 – 500 000 = 175 000 (руб.).