Эквивалентность процентных ставок различного типа

Часто при расчетах, проводимых по различным финансовым операциям, возникает необходимость в определении эквивалентных процентных ставок.

Эквивалентные процентные ставки – это такие процентные ставки разного вида, применение которых при одинаковых начальных условиях дает одинаковые финансовые результаты.

Эквивалентные процентные ставки необходимо знать в случаях, когда существует возможность выбора условий финансовой операции и требуется инструмент для корректного сравнения различных процентных ставок.

Для нахождения эквивалентных процентных ставок используют уравнения эквивалентности, принцип составления которых заключается в следующем. Выбирается величина, которую можно рассчитать при использовании различных процентных ставок (обычно это наращенная сумма S). На основе равенства двух выражений для данной величины и составляется уравнение эквивалентности, из которого путем соответствующих преобразований получается соотношение, выражающее зависимость между процентными ставками различного вида.

Вспомним обозначения, использованные ранее:

i − простая годовая ставка ссудного процента;

d − простая годовая учетная ставка;

iс − сложная годовая ставка ссудного процента;

dс − сложная годовая учетная ставка;

j − номинальная ставка ссудного процента;

f − номинальная учетная ставка.

Повторим формулы для определения наращенной суммы при различных способах начисления процентов, полученные ранее:

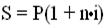
; (1.7)

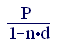
S = (2.5)

S = P (1+iс) 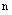. (3.1)

S m n = P (1 + j/m) , (3.6)

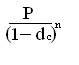
S = (4.1)

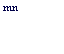S = P/ (1- f/m ) (4.5)

Приравнивая эти формулы попарно, можно получить соотношения, выражающие зависимость между любыми двумя различными процентными ставками.

Рассмотрим несколько случаев.

Приравнивая соотношения (1.7) и (2.5), получим

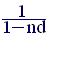
1 + n i = ,

откуда

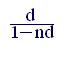
i = ; (5.1)

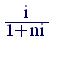
d = . (5.2)

Из формул (1.7) и (3.1) имеем

1 + n i = (1 + iс) ;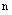

i = [(1 + ic) – 1] / n; (5.3)

iс = 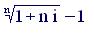(5.4)

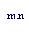Приравнивание формул (1.7) и (3.6) дает

1 + n i = (1 + j/m) ;

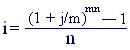
(5.5)

j = m ( 1 + ni − 1). (5.6)

Для различных случаев сложных процентов получаем уравнение эквивалентности, приравнивая формулы (3.1) и (3.6):

(1 + ic) = (1 + j/m) ;

ic = (1 + j/m) – 1; (5.7)

j = m ( 1 + ic – 1). (5.8)

Полученная по формуле (5.7) годовая ставка сложных процентов, эквивалентная номинальной процентной ставке, называется эффективной ставкойсложных процентов.

Эффективную ставку сложных процентов полезно знать, чтобы оценить реальную доходность финансовой операции, или сравнить процентные ставки в случае, когда используются различные интервалы начисления. Очевидно, что значение эффективной процентной ставки больше значения номинальной, а совпадают они при m = 1.

Далее из формул (3.1) и (4.1) имеем

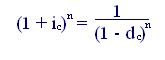
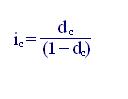; (5.9)

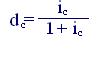
. (5.10)

Аналогичным образом получаем зависимости между любыми другими эквивалентными ставками.

Проанализировав полученные формулы, можно сделать два замечания:

1. Эквивалентность различных процентных ставок никогда не зависит от величины первоначальной суммы p (для данного рассматриваемого случая, когда первоначальная сумма p предполагается одинаковой).

2. Эквивалентность процентных ставок всегда зависит от продолжительности периода начисления за исключением случая эквивалентности между собой сложных процентных ставок разного вида (если период начисления один и тот же).

Используя для вычислений формулы (3.1) и (4.1), можно построить таблицу, отражающую зависимость между эквивалентными ставками и ставками ссудных процентов (см. приложение, табл.2). Видно, что небольшие учетные ставки имеют эквивалентные ставки ссудного процента, сопоставимые по величине, но сростом учетных ставок разница увеличивается очень быстро.

Можно определить также процентную ставку, эквивалентную данной, когда начальные условия полностью или частично не совпадают. Данная ситуация может возникнуть, например, если есть возможность выбора между различными коммерческими предложениями.

Рассмотрим следующую задачу:

Какова должна быть сложная учетная ставка dс, чтобы сумма P1, вложенная под эту ставку на n1 лет, достигла той же величины, что и сумма P2, вложенная под сложную ставку ссудного процента iс на n2 лет?

Поскольку финансовые результаты обеих операций должны быть равны, составляем следующее уравнение эквивалентности:

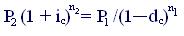
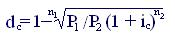Отсюда

(5.11)

Можно решить уравнение относительно i, тогда

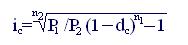
(5.12)

Аналогичные зависимости можно получать для любых видов процентных ставок.

Принцип эквивалентности также используется при решении вопросов финансовой эквивалентности платежей.

Как определить, что выгоднее, заплатить сумму S1 через n1 лет или сумму S2 через n2 лет? Будем считать, что S1 < S2 и n1 < n2 (иначе задача имеет тривиальное решение).

В зависимости от размера процентной ставки (возьмем для примера сложную ставку ссудного процента), под которую могут быть вложены деньги, суммы S1 и S2 имеют различные современные величины P1 и P2:

.

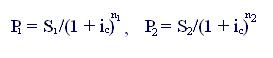
Очевидно, что для ic = 0 S1 = P1 и S2 = P2.

В этом случае выгоднее выплачивать меньшую сумму S1. Поскольку n1 < n2, для достаточно больших ic будет выполняться P1 > P2 (см.рис.4). Тогда найдётся i0, уравнивающая ставка, при которой современные величины обеих сумм совпадут.

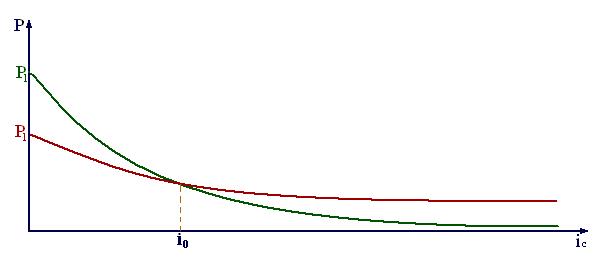
Рис. 4

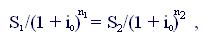
Т.е.

откуда

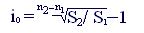(5.13)

Для всех ic < i0 предпочтительнее вариант с меньшей суммой и меньшим сроком. Для ic > i0 − с большими. При ic =i0 финансовые результаты обеих операций эквивалентны.

Аналогичные формулы могут быть получены для всех видов процентных ставок.

ПРИМЕР 15

Срок уплаты по долговому обязательству – полгода, учётная ставка равна 18%. Какова доходность данной операции, измеренная в виде простой ставки ссудного процента?

Решение:

Используем формулу (5.1):

i = 0,18/(1-0,5∙0,18) = 0,198= 19, 8%

ПРИМЕР 16

Рассчитать эффективную ставку сложных процентов, если номинальная ставка равна 24% и начисление процентов происходит ежемесячно.

Решение:

Вычисление проводим по формуле (5.7):

ic= (1+0,24/12) − 1 = 0,268 = 26,8%.

ПРИМЕР 17

Определить под какую ставку процентов выгоднее поместить капитал в 10 000 000 руб. на пять лет:

а) под простую ставку процентов 30% годовых;

б) под сложную ставку в 25% при ежеквартальном начислении?

Решение:

В данном случае не обязательно считать величину наращенной суммы, получаемой при различных процентных ставках. Поэтому не важна величина первоначального капитала. Достаточно найти, например, простую процентную ставку, эквивалентную данной сложной ставке, воспользовавшись формулой (5.5):

i= [(1+0.25/4) − 1] / 5 = 0.472=47, 2%.

Так как простая процентная ставка (47,2%), которая дала бы одинаковый с данной сложной процентной ставкой результат, значительно превышает предложенную (30%), ясно, что гораздо выгоднее использовать сложную процентную ставку. Подсчитаем теперь наращенные суммы, получаемые в обоих случаях, чтобы выяснить, насколько более выгодна сложная ставка. Используем для этого формулы (1.7) и (3.6):

а) S = 10 000 000∙(1 + 5∙0,3) = 25 000 000 (руб.)

б) S = 10 000 000∙(1 + 0,25/4) = 33 618 521 (руб.)

Ощутимая разница в результатах подтверждает сделанный ранее вывод. Можно заметить, что решение примера с использованием эквивалентных процентных ставок требует в два раза меньше вычислений.

ПРИМЕР 18

Определить номинальную ставку процентов, которая обеспечивала бы годовую доходность в 26%, если начисление процентов происходит ежемесячно.

Решение

По формуле (5.8) получаем

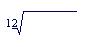j = 12( 1+ 0,26 − 1) = 0,234 = 23,4%.

ПРИМЕР 19

Капитал, взятый в кредит, вложен под сложную ставку ссудного процента 22% годовых. Для расчета с кредиторами необходимо выплатить 30 000 000 через два года или 36 000 000 через три года. Какой вариант предпочтительнее?

Решение

По формуле (5.13) найдем уравнивающую процентную ставку i0:

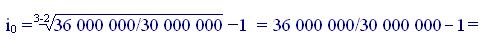
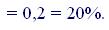
Данная нам ставка 22% больше найденной, следовательно, современная величина второй (большей) суммы оказывается меньше, предпочтительнее отдать её через три года.