Примеры решения типовых задач. Предприятие рассматривает целесообразность приобретения новой технологической

Задача 1.

Предприятие рассматривает целесообразность приобретения новой технологической линии по цене 18000 тыс. руб. По прогнозам сразу же после пуска линии ежегодные поступления после вычета налогов составят 5700 тыс. руб. Работа линии рассчитана на 5 лет. Ликвидационная стоимость линии равна затратам на ее демонтаж. Необходимая норма прибыли составляет 12% (т.о. требуется определить целесообразность).

Чистая текущая стоимость проекта определяется по формуле:

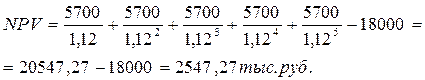
Представим данный расчет с помощью следующей схемы:

Таким образом, эта задача решается с использованием формулы приведенной величины обычной ренты. Общая накопительная величина дисконтированных доходов (поступлений) 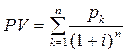равна приведенной величине обычной ренты 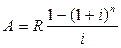. Отсюда 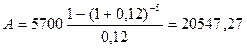тыс. руб.

Так как величина чистой текущей стоимости 20547,27-18000=2547,27>0, то проект может быть принят.

Задача 2.

Имеются два инвестиционных проекта, в которых потоки платежей на конец года характеризуются данными представленными в табл.7.1.

Таблица 7.1 – Потоки платежей на конец года.

Проект	Годы
1-й	2-й	3-й	4-й	5-й	6-й	7-й	8-й
А Б	-200 -400	-300 -100						-

Требуется определить более предпочтительный проект. Ставка сравнения (норматив рентабельности) принята в размере 10%.

NPV_А=(-200)×1,1^-1+(-300)×1,1^-2+100×1,1^-3+300×1,1^-4+400×1,1^-5+ +400×1,1^-6+350×1,1^-7=-429,75+933,8=504,05 тыс. руб.

NPV_Б=(-400)×1,1^-1+(-100)×1,1^-2+100×1,1^-3+200×1,1^-4+200×1,1^-5+ +400×1,1^-6+400×1,1^-7+350×1,1^-8=-429,75+933,8=504,05 тыс. руб.

Из двух проектов, проект А более предпочтителен, так как он имеет большее значение NPV.

Если вложения и поступления равномерные и дискретные, причем доходы начинают поступать сразу же после завершения вложений, то величина NPV находится как разность современных величин двух рент.

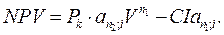Здесь: P_k – доходы в периоды 1,2,…,n₂;

CI – инвестиционные расходы в периоде 1,2,…,n₁;

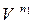^– коэффициент дисконтирования по ставке приведения –i;

n₁ – продолжительность периода инвестиций;

n₂ – продолжительность получения отдачи (дохода) от инвестиций;

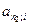– коэффициент приведения ренты.

Задача 3.

Инвестиции производятся поквартально по 0,5 млн. руб. на протяжении 3-х лет (n₁=3 года; CI=0,5×4=2,0 млн. руб. в год; P₁=4). Доходы начинают поступать сразу же после завершения вложений. Ожидаемая отдача оценена в размере 1,3 млн. руб. в год. Поступления ежемесячные в течении 8 лет, т.е. параметры второй ренты: CI=1,3; n₂=8; P₂=12. Норматив рентабельности –12%. Требуется определить эффективность проекта.

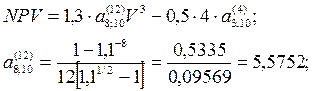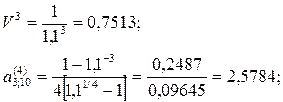NPV=1,3×5,5752×0,7513-0,5×4×2,5784=5,4452-5,1568=

=0,2884 млн. руб.

Графически этот процесс может быть изображен следующим образом:

Период от начала инвестиций до конца срока поступления доходов – 11 лет (3+8). Величина 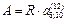показывает, какая сумма доходов должна быть после окончания инвестиций, т.е. после третьего года. Эта сумма обеспечивает наращение к концу срока полученных доходов – A(1+i)ⁿ=S. Чтобы устранить влияние фактора времени (3 года), данную сумму необходимо дисконтировать с использованием множителя V³. Иначе говоря, из современной величины отсроченной ренты (дохода) вычитается современная величина немедленной ренты.

В случае, когда вложения и отдачу можно рассматривать как непрерывные процессы и если получение отдачи происходит сразу же после окончания вложений, чистый приведенный доход будет равен:

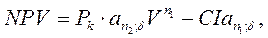где 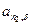– коэффициент приведения непрерывной ренты.

Сила роста составит d=ln 1,1=0,095531. Тогда:

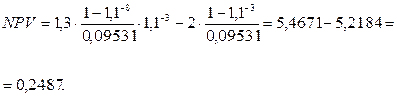
Если же отдача (доходы) от инвестиций будет получена не сразу после их окончания, а, например, через год, то чистый приведенный эффект (доход) значительно ниже.

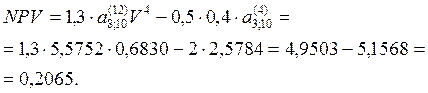Как видим, отсрочка в получении доходов на 1 год делает проект убыточным.

Срок окупаемости (payback period method – PP) – один из наиболее часто применяемых показателей для анализа инвестиционных проектов.

Если не учитывать фактор времени, т.е. когда равные суммы дохода, получаемые в разное время, рассматриваются как равноценные, то показатель окупаемости можно определить по формуле:

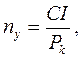
где n_y – упрощенный показатель срока окупаемости;

CI – размер инвестиций;

P_k – ежегодный чистый доход.

Иначе говоря, период окупаемости PP – продолжительность времени, в течение которого недисконтированные прогнозируемые поступления денежных средств превысят сумму инвестиций, т.е. это число лет, необходимых для возмещения стартовых инвестиционных расходов.

Задача 4.

Предположим, произведены разовые инвестиции в размере 38 тыс. руб. Годовой приток планируется равномерным в размере 10, 7 тыс. руб. Тогда

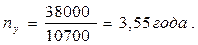
Если же годовые поступления наличности не равны, то расчет окупаемости осложняется.

Предположим, что годовые притоки распределены по годам следующим образом (табл. 6.2.).

Таблица 7.2 – Потоки платежей по проекту

Годы	1-й	2-й	3-й	4-й	5-й
Поступление наличности тыс. руб.

Сумма поступлений за первые три года составит:

8000+12000+12000=32000 тыс. руб.,

т.е. из первоначальных инвестиций остается невозмещенными 38000 – 32000 = 6000 тыс. руб. Тогда при стартовом объеме инвестиций в размере 38000 тыс. руб. период окупаемости составит:

3 года + 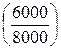= 3,75 года.

Если рассчитанный период окупаемости меньше максимально приемлемого, то проект принимается, если нет – отвергается. Если бы в нашем примере необходимый период окупаемости был 4 года, проект был бы принят.

Рассмотрим определение срока окупаемости для доходов, которые можно представить в виде некоторых упорядоченных последовательностей (аннуитетов). Начнем с самого простого случая – с равномерного, дискретного (один раз в конце года) поступления доходов. Из условий полной окупаемости за срок n_ok при заданной ставке i следует равенство суммы капитальных вложений современной стоимости аннуитета.

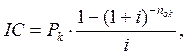отсюда:

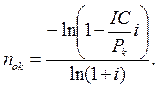Аналогичным путем можно найти срок окупаемости для других видов распределения отдачи. В каждом таком случае капиталовложения приравниваются к современной величине финансовых рент, т.е. IC равно A, а члены денежного потока P_k равны R – члену ренты (число членов потока в год – P).

Задача 5.

Инвестиции к началу поступления доходов составили 6 млн. руб., годовой доход ожидается на уровне 1,05 млн. руб., поступления ежемесячные, при принятой ставке сравнения i=10%.

Исходя из формулы для расчета срока постоянных рент, постнумерандо будет равно:

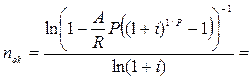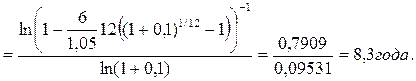Для сравнения заметим, что без учета фактора времени получения доходов срок окупаемости составит 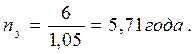Как видим, разница существенная. Не всякий уровень дохода при прочих равных условиях приводит к окупаемости инвестиций.

Задача 6.

Требуется определить значение IRR (процентную ставку) для проекта, рассчитанного на 3 года, требующего инвестиции в размере 20 млн. руб. и имеющего предполагаемые денежные поступления в размере p₁=3 млн. руб. (первый год), p₂=8 млн. руб. (второй год) и p₃=14 млн. руб. (третий год).

Для решения задачи воспользуемся формулой:

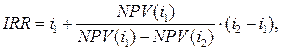где i₁ – значение процентной ставки в дисконтном множителе, при котором NPV(i₁)<0; NPV(i₁)>0;

i₂ – значение процентной ставки в дисконтном множителе, при котором NPV(i₂)<0; NPV(i₂)>0.

Возьмем два произвольных значения процентной ставки для коэффициента дисконтирования: i₁=15% и i₂=20%.

Соответствующие расчеты приведены в табл. 7.3 и 7.4.

Таблица 7.3 – Расчет показателей эффективности проекта

Год t	По- ток	Расчет I	Расчет II
i1=15%	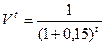NPV(i) =	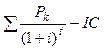i1=20%	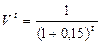NPV(i) =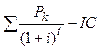
0-й 1-й 2-й 3-й	-20 6,0 8,0 14,0	1,0 0,8696 0,7561 0,6575	-20,0 5,2176 6,0488 9,2050	1,0 0,8333 0,6944 0,5787	-20,0 4,9998 5,5552 8,1018
0,4714	-1,3432

Таблица 7.4 – Расчет показателей эффективности проекта

Год t	По- ток	Расчет I	Расчет II
i1=16%	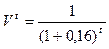NPV(i) =	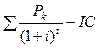i1=17%	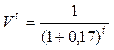NPV(i) =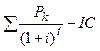
0-й 1-й 2-й 3-й	-20 6,0 8,0 14,0	1,0 0,8662 0,7432 0,6407	-20,0 5,1972 5,9200 8,0698	1,0 0,8547 0,7305 0,6244	-20,0 5,1282 5,8440 8,7416
0,0870	-0,2862

По данным расчета I и II вычислим значение IRR.

1)

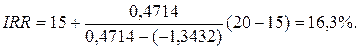
Уточним величину ставки, для чего примем значения процентных ставок, равные i₁=16% и i₂=17%. Произведем новый расчет.

2)

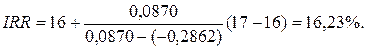
IRR=16,23% является верхним пределом процентной ставки, по которой фирма может окупить кредит для финансирования инвестиционного проекта. Для получения прибыли фирма должна брать кредит по ставке менее 16,23%.

Задача 7.

Показатели современных величин вложений 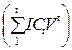равны 5,1568 млн. руб., а современная величина чистых доходов 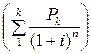составляет 5,4452 млн. руб.

При этих условиях индекс рентабельности будет равен

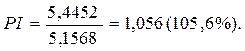
Если показатель PI=1, то это значит, что доходность инвестиций точно соответствует нормативу рентабельности (ставке сравнения).

При PI<1 инвестиции нерентабельны, так как не обеспечивают этот норматив.