Ценные бумаги денежного рынка

Ценные бумаги денежного рынка (векселя, государственные краткосрочные облигации) являются краткосрочными ценными бумагами, платежи по которым осуществляются в день погашения. С точки зрения оценки они финансово эквивалентны облигациям с дисконтом. По многим ценным бумагам денежного рынка цена определяется в терминах их дисконтной доходности.

Формула дисконтной доходности

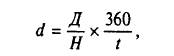
где Д — дисконт от номинала (Д = Н — Р);

Н — номинал;

t — число дней до погашения ценной бумаги.

Д = 100% / H — процентный дисконт от номинала, т.е. та доходность, которую инвестор получит за I дней, оставшихся до погашения ценной бумаги. Второй множитель показывает число раз, если 7 дней укладывается в количество дней в году (например, в 360 дней). Так, при номинале 100 тыс. долл., дисконте (Д) 3 тыс. долл. и если до погашения осталось 90 дней, дисконтная доходность погашения (по простой процентной ставке) составит 12 % (d = 3% х 4 = 12%). Поскольку цена дисконтной ценной бумаги зависит от номинала и дисконта, то она может быть выражена в терминах дисконтной доходности:

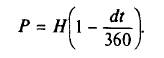
Зная дисконтную доходность, это выражение можно использовать для расчета цены, которую инвестор заплатит за ценную бумагу: Р = 100 тыс. х (1 -- (0,12 х 90) /360) = 97 тыс. долл.

Хотя понятие простой дисконтной доходности широко используется на денежном рынке, существует ряд концептуальных проблем.

1. Дисконт рассчитывается на денежную единицу номинала, а не цены. В приведенном выше примере предполагается, что дисконтная доходность за 90 дней составит 3% (3 тыс. / 100 тыс.), хотя фактически инвестор получит доходность 3,09% (3 тыс. / 97 тыс.), так как инвестировано 97 тыс. долл.

2. Существуют различные системы учета числа дней в году и в месяце. Немецкая и французская системы отличаются округлением количества дней на рассматриваемом промежутке времени. Самая точная англо-американская система не допускает никаких округлений (берется реальное число дней в году: 365 или 366 и календарное число дней в месяце: 28, 29, 30, 31). Немецкая система расчета (наиболее широко используемая) предполагает, что в году 360 дней, а в месяце — 30.

3. Формула дисконтной доходности не учитывает временную стоимость денег, так как просто перемножается доходность /дней на число /-дневных периодов в году. В результате дисконтная доходность может отличаться от истинной доходности рассматриваемой ценной бумаги.

Переход на иную систему учета временных периодов осуществляется через введение понятия эквивалентной облигационной доходности (equivalent bond yield - EBY):

Из уравнения d = (Д/Н)( 360/г) получим Д, из Р= Н (1 – dt/360) получим Р, и таким образом:

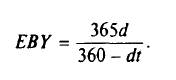
Для рассматриваемого 90-дневного инструмента ЕВY= (365 х 0,12) / (360 - 0,12 х 90) = 12,54%. Эквивалентная облигационная доходность, так же как и простая дисконтная доходность, не учитывает временную стоимость денег.

Истинная доходность к погашению k, или эффективная доходность, которую инвестор получает, вкладывая в дисконтную облигацию или дисконтный инструмент денежного рынка Р денежных единиц сегодня, рассчитывая на момент погашения через t дней получить номинал H, может быть оценена из уравнения Р (1 + k)1/360 = Н, где k — доходность к погашению, рассчитанная по правилу сложного процента. Эффективная годовая доходность отражает доход, который инвестор может иметь за год при условии реинвестирования полученных средств по действующей ставке. Это уравнение можно решить относительно k и выразить в терминах простой дисконтной доходности d и числа дней функционирования облигации:

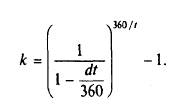
Например, для 90-дневной облигации с номиналом 100 тыс. долл. и ценой 97 тыс. долл. эффективная доходность составит 97 (1 + k)90/360 = 100, k = 13,15%, что на 1% превышает простую дисконтную доходность.

Включение в рассмотрение возможности реинвестирования обеспечивает в расчетах инвестора повышенную доходность. Чем больше период предполагаемого владения до погашения (t в днях), тем ближе значения доходности к погашению и эффективной доходности. Например, по данным биржевых u1090 торгов Санкт-Петербургской валютной биржи от 23 декабря 1996 г., по облигациям Администрации Санкт-Петербурга (ГГКО) расчет позволил получить значения доходности, приведенные в табл. 4.3.

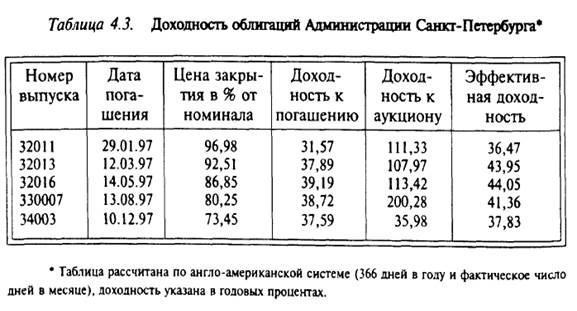
Эффективная доходность является важным инструментом принятия решений на рынке ГКО, так как позволяет определить недооцененность или переоцененность краткосрочных облигаций с близкими сроками погашения и близкими значениями котировок. Например, по табл. 4.3 видно, что ГКО-34003 переоценена, так как эффективная доходность по ней ниже оценки по выпускам 32013, 32016 и 330007.