Теорема умножения вероятностей

ТЕОРИЯ ВЕРОЯТНОСТЕЙ И

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Методические указания к проведению практических занятий

по теории вероятностей и математической статистики для направления ЭКОН

Балаково 2015

Введение

Методические указания к проведению практических занятий по теме «Теория вероятностей» предназначены для направления ЭКОН заочной формы обучения. Они содержат основные теоретические сведения по теме «Теория вероятностей и математическая статистика», образцы решения типовых заданий. Кроме того, в методических указаниях приведены вопросы для самопроверки, список литературы, необходимой для изучения данной дисциплины.

Цель работы:

- оказание помощи студентам в усвоении и закреплении практических навыков решения задач по дисциплине «Теория вероятностей и математическая статистика»;

- формирование общекультурных и профессиональных компетенций;

- приобретение знаний для дальнейшего изучения других дисциплин.

Классическое определение вероятности событий

Пример 1. Пусть в урне имеется 12 белых и 7 черных шаров. Какова вероятность извлечь белый шар?

Решение. При выборе шара равновозможно извлечь любой из 19 шаров, n=19. Из этих 19 шаров белого цвета 12, т.е. m=12. Таким образом, вероятность вынуть белый шар равна: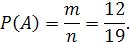

Аналогично, вероятность извлечь черный шар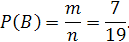

Теорема сложения вероятностей

Пример 2. В денежно-вещевой лотерее на каждые 1000 билетов разыгры­вается 100 вещевых и 10 денежных выигрышей. Определить вероятность денежного или вещевого выигрыша на один лотерейный билет.

Решение.Обозначим: А – событие, состоящее в том, что выиграна вещь, вероятность этого события: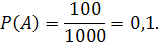

Событие В – выиграны деньги: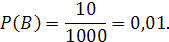

События А и В несовместные, так как один билет может выиграть либо вещь, либо деньги. Событие А+В состоит в выигрыше или вещи, или денег. Согласно теореме сложения вероятностей для несовместных событий находим: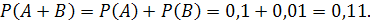

Теорема умножения вероятностей

Пример 3.Имеется 10 радиоламп, среди которых 3 неисправные, на вид не отличающиеся от новых. Наугад выбирают друг за другом две лампы. Какова вероятность того, что обе лампы окажутся исправными.

Решение.Пусть событие А₁ состоит в том, что первая лампа окажется исправной. Вероятность Р(А₁) = 7/10.

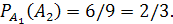Событие А₂ – вторая лампа исправна. Вероятность второго события будет зависеть от события А₂.:

Событиe А₁А₂ состоит в том, что обе лампы исправны. Применяем теорему умножения вероятностей зависимых событий:

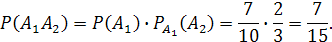
Пример 4.Прибор состоит из двух узлов, которые во время работы могут независимо друг от друга выходить из строя. Пусть вероятность безотказ- ной работы первого узла в течение гарантийного срока равна 0,7, а второго 0,9. Найти вероятность того, что в течение гарантийного срока прибор будет работать исправно.

Решение.Прибор работает исправно, если два узла работают без сбоев. Пусть событие А₁ состоит в том, что первый узел работает Р(А₁) = 0,7. Событие А₂ – второй узел работает Р(А₂) = 0,9. Тогда, вероятность того, что оба узла работают, найдем по теореме умножения вероятностей независимых событий: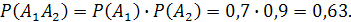

Пример 5.Студент знает 20 вопросов из 40 по первому разделу и 40 из 50 вопросов по второму разделу. На экзамене ему случайным образом предлагается ответить на вопросы из обоих разделов. Найти вероятность того, что студент ответит правильно: 1) на оба вопроса; 2) только на один вопрос; 3) хотя бы на один вопрос.

Решение. 1. Пусть событие А состоит в том, что студент ответит правиль­но на вопрос из первого раздела. Р(А) = 20/40 = 0,5.

Событие В – студент ответит верно на вопрос второго раздела

Р(В) = 40/50 = 0,8. Вероятность события В не зависит от того, ответит студент или нет на вопрос из первого раздела. События А и В независимы.

Событие АВ – студент ответит правильно на оба вопроса.

По теореме умножения вероятностей независимых событий:

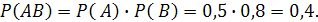
2. Событие “Студент ответит правильно только на один вопрос” рас­кладывается на элементарные события: 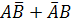(студент ответит правиль но на вопрос из первого раздела и неправильно на вопрос второго раздела или ответит неправильно на вопрос первого раздела и правильно на вопрос второго раздела). Событие 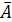– студент ответит неправильно на вопрос первого раздела. Р( 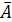) = 20/40 = 0,5. Событие 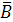– студент ответит неправильно на вопрос второго раздела. Р( 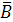) = 10/50 = 0,2.

Тогда по теореме сложения вероятностей несовместных событий и теореме умножения вероятностей независимых событий, получим: Р( 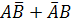) = Р(А) 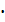Р( ) + Р( 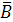) Р(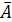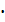В) = 0,5 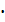0,2 + 0,5 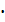0,8 = 0,5.

3. Событие A+B –студент ответит правильно хотя бы на один вопрос. Вероятность события A+B можно найти тремя способами.

1 способ решения.Событие A+B возможно разложить на элементар­ные события : AB +A 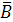+ 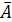B. Тогда:

P(AB + A 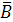+ 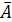B) = P(A) P(B) + P(A) P( 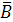) + P( 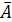) 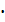P(B) = 0,5 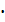0,8 + 0,5 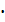0,2+ +0,5 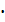0,8 = 0,9.

2 способ решения. Событие A+B противоположно событию 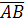- студент не ответит на вопросы обоих разделов. Воспользуемся формулой:

P(A+B) = 1 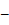P ( 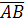) = 1 – 0,5 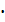0,2 = 0,9.

3 способ решения.Так как события A и B совместные и независи­мые, воспользуемся теоремой сложения вероятностей двух совместных со­бытий: P(A+B) = P(A) + P(B) - P(AB) = 0,5 + 0,8 – 0,5 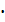0,8 = 0,9.