Наращение по простой ставке процентов (прямая задача)

Теоретические основы финансовой математики

Основной задачей финансовой математики является приведение в соответствие размеров и сроков платежей со временем расчетов и правилами сделки.

Основной категорией финансовой математики является процент, как причина изменения стоимости денег во времени.

В практике финансовой математики используют ряд важных характеристик.

Процентные деньги ( проценты) – это абсолютная величина дохода от предоставления денег в долг.

Процентная ставка – это отношение процентных денег, выплачиваемых за фиксируемый период, к величине капитала (долга).

Период начисления – это временной интервал, к которому приурочена процентная ставка.

Способы начисления процентов зависят от условий контрактов.

Классификация процентов (процентных ставок)

Относительно базы начисления

· простые –при постоянной базе, т.е. весь срок обязательства начисляются на постоянную сумму;

· сложные - при переменной базе, т.е. за базу принимается сумма, полученная на предыдущем этапе, проценты начисляются на проценты.

2. Относительно момента выплаты или начисления дохода

· обычные (по ставке наращения, декурсивные) –начисляются в конце периодов финансовой операции относительно исходной величины средств;

· авансовые ( по учетной ставке, антисипативные) –проценты выплачиваются в момент предоставления кредита, в начале периода.

Простые проценты

Наращение по простой ставке процентов (прямая задача)

Условные обозначения:

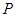- исходная стоимость денег;

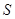- наращенная сумма денег через определенный период;

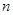- число процентных периодов;

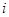- процентная ставка за период.

Наращенная сумма денег( 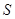) – это сумма денег, увеличенная в связи с присоединением процентов. Такой процесс присоединения суммы денег называется наращением.

Ситуация 1: периоды определены в годах.

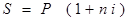, (1)

где 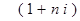- множитель наращения,

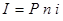- проценты.

Ситуация 2: задана годовая ставка, а срок операции выражен в днях или в месяцах.

Вместо 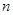в формулу (1) подставим ,

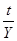где 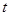- срок операции в днях или месяцах;

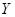- продолжительность года в тех же единицах, что и .

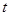Тогда 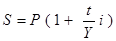. (2)

При этом 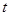и 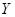, если они измеряются в днях, могут быть выражены точно или приближенно, поэтому существует три варианта простых процентов для ситуации 2.

1. Точные проценты с фактическим сроком операци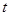и: и 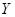измерены точно (обозначение – 365/365). Число дней месяца определяется как разность номеров дней окончания и начала операции, число дней года – 365 или 366.

2. Обыкновенные проценты с точным числом дней операции: 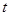- точно, 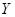- приближенно, 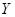= 360 (обозначение 365/360).

3. Обыкновенные проценты с приближенным сроком операци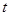и: и 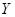измерены приближенно (обозначение 360/360). При определении 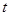число дней в полных месяцах периода берется равным 30, в неполных – по факту, а день начала и окончания операции считается за один день.

Ситуация 3: простая ставка меняется во времени.

,

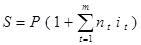где 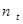- продолжительность 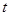- го периода, ;

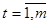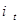- ставка простых процентов в периоде ,

.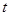
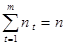