Розрахункові суми для оцінки ліній регресії.

№ ознаки	х	у	xy			Y
. . .
Разом						x

Із складеної нормальної системи рівнянь:

а = `y - b`x

Параметр 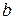– коефіцієнт регресії, який вказує, на скільки одиниць в середньому змінюється Y із зміною х на одиницю. У випадку прямого зв’язку 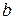– величина додатна, а при зворотному - від’ємна. Параметр а- вільний член рівняння регресії, це значення У при х=0.

Мірою тісноти зв’язку в кореляційно - регресійному аналізі виступає коефіцієнт детермінації , який відображає частку факторної дисперсії у загальній.

Дисперсію теоретичних значень (факторну) визначають за формулою:

Загальна дисперсія ознаки дорівнює:

Коефіцієнт детермінації характеризує ту частину варіації результативної ознаки у, яка відповідає лінійному рівнянню регресії і змінюється в межах 0£ R£1. Індекс кореляції характеризує тісноту зв’язку але економічної інтерпретації не має.

Лінійний коефіцієнт кореляції розраховується за формулою

Перевірку істотності зв’язку в кореляційно - регресійному аналізі здійснюють за допомогою критичних значень та F-критерію. Фактичне значення F–критерію розраховують за формулою.

Ступені вільності залежать від параметрів рівняння (m): k₁=m-l, k₂=n-m.

Для лінійної моделі Y = a + bx, m=2.

У невеликих щодо обсягу сукупностях коефіцієнт регресії схильний до випадкових коливань. Тому необхідно визначати довірчі межі коефіцієнта регресії. Стандартна помилка коефіцієнта регресії обчислюється за формулою:

Величина граничної помилки

де t- коефіцієнт довіри, визначається для ймовірностей 0,95 , або 0.954 (1.96 і 2.00);

залишкова дисперсія, яка визначається за формулою.

або

і характеризує варіацію результативної ознаки у, не пов’язану з варіацією факторної ознаки х. Довірчі межі коефіцієнта регресії складають:

Якщо х збільшується на одиницю, рівень у лишається в наведених даних. В кінці рішення задачі прикладається графік кореляційного поля і лінії регресії Y = a + bx.

ІІ Завдання до індивідуальних робіт.

Задача №1.

1. За наведеними даними про суму капіталу і прибуток 100 комерційних банків складіть:

а) комбінаційний розподіл банків за цими ознаками, утворивши п’ять групи з рівними інтервалами; за результатами групувань зробіть висновок про наявність та напрямок зв’язку між ознаками;

б) аналітичне групування, яке б показало залежність прибутку від суми капіталу.

Результати групувань подати у вигляді статистичних таблиць та гістограми. Зробити висновки.

Вхідні дані подані в таблиці 2.1

Табл. 2.1.

Капітал та прибуток 100 комерційних банків регіону у звітному році. *

№ банку	Капітал, млн. грн.	Прибуток, млн. грн.	№ банку	Капітал, млн. грн.	Прибуток, млн. грн.
	10,26	10,8		12,42
	10,62	12,6		16,02	22,14
	12,06			5,4	6,3
	10,44	13,86		10,26	7,92
	12,78	19,08		6,66	6,84
	14,76	19,98		10,08	15,84
	12,78			8,1	8,1
	11,88	16,92		4,5	4,68
	13,86	18,36			25,02
	10,26	14,04		12,78	17,28
	13,68	19,08		11,7	12,24
	9,9	10,62		13,5	17,82
	16,56	17,1		12,78	17,28
	10,08	13,68		14,94	18,9
	11,16	12,42		10,08	16,02
	10,62	12,78		8,28	12,6
	14,94	19,62		10,98	14,4
	10,8	12,24		5,4	4,5
	12,6	18,18		12,42	16,56
	7,2			11,7	12,42
	12,78	16,92		7,38	7,74
	17,1	20,16		7,38	7,92

Продовження табл. 2.1

	9,9	13,14		7,56	10,8
	12,96	17,1		7,38	13,5
	13,68	19,26		10,08	16,02
	9,54	11,52		12,6	18,18
	12,78	15,66		15,84	21,42
	14,94	16,56		5,76	6,66
	12,06	12,6		9,63	10,08
	12,96	16,74		6,3	6,66
	11,88	12,6		10,44	16,2
	11,34	13,32		7,74	7,74
	13,14	16,92		12,96	17,1
	11,16	11,88		4,32	4,5
	13,32	16,92		17,64	24,48
	11,34	12,78		11,34	12,06
	10,62	12,6		13,32	17,64
	11,16	12,42		12,6	17,1
	10,26	13,32		14,76	19,08
	11,52	12,78		10,08	15,84
	10,44	11,34		7,92	12,42
	11,7	14,4		10,8	14,58
	10,26	10,8		5,58	4,68
	12,06	13,14		12,06	16,2
	10,8	12,78		11,52	12,06
	9,54	12,6		7,2	7,56
	14,22	16,92		7,56	8,28
	9,36	12,24		7,74	10,8
	9,54	15,12		7,56
	11,34	12,96		9,54	10,44

*Студент обов’язково змінює наведені дані збільшуючи обсяги капіталу по кожному банку на 0,9. (замість крапки слід поставити останню цифру залікової книжки студента.)

Задача 2.

Варіанти вибірок для завдань наведені в табл. 2.2.

Табл.2.2.