Раздел 2. Теория вероятностей

ТЕОРИЯ ВЕРОЯТНОСТЕЙ

И

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА

Организационно-методический раздел

Цель курса

Данный курс имеет целью ознакомить студентов с основами математического аппарата теории вероятностей и математической статистики, необходимого при решении теоретических и практических задач по указанной специальности, выработать у студентов навыки к математическому исследованию экономических проблем.

Задача курса

Научить студентов использовать количественные методы обработки статистической информации, проверять статистические гипотезы, строить оценки параметров генеральной совокупности.

Место курса в профессиональной подготовке выпускника

Курс является обязательной дисциплиной и читается в третьем семестре.

Требования к уровню освоения содержания курса

В результате освоения курса студент должен уметь определять вероятности событий, строить точечные и интервальные оценки параметров функции распределения, проверять простейшие статистические гипотезы, строить простейшие регрессионные модели.

Содержание курса

Разделы курса

Раздел 1. Элементы комбинаторики.

Раздел 2. Теория вероятностей.

Раздел 3. Математическая статистика.

Темы и краткое содержание

Раздел 1. Элементы комбинаторики.

Тема 1. Правила умножения и сложения. Размещения, сочетания, перестановки. Их свойства.

Раздел 2. Теория вероятностей

Тема 2. Случайные события.

Понятие «событие». Типы событий: случайные, достоверные, невозможные, совместные - несовместные, противоположные, равновозможные. Полная группа событий, элементарные события.

Тема 3. Операции над случайными событиями.

Сумма и произведение событий. Диаграммы Венна. События, совместные в совокупности.

Тема 4. Классическое определение вероятности.

Вероятность наступления случайного события. Статистическая вероятность. Геометрическая вероятность.

Тема 5. Теоремы сложения и умножения вероятностей.

Вероятность суммы двух несовместных событий. Сумма вероятностей попарно несовместных событий, образующих полную группу событий.

Вероятность двух совместных событий.

Условная вероятность. Теорема умножения вероятностей.

Тема 6. Независимые события.

Определение независимости двух событий. Критерий независимости двух событий. Свойства независимости событий.

События независимости в совокупности. Вероятность наступления хотя бы одного события.

Тема 7. Формула полной вероятности. Формула Байеса.

Тема 8. Повторные испытания.

Формула Бернулли. Локальная теорема Муавра-Лапласа. Теорема Пуассона. Интегральная теорема Муавра-Лапласа.

Тема 9. Случайной величины.

Понятие случайные величины. Типы случайных величин. Операции над случайными величинами. Закон распределения случайных величин. Функция распределения случайных величин, ее свойства. Функция плотности распределения случайных величин, ее свойства. Основные законы распределения: нормальное, 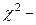распределение, распределение Стьюдента, распределение Фишера, равномерное распределение.

Числовые характеристики случайных величин. Математическое ожидание, его свойства. Дисперсия, ее свойства. Среднеквадратичное отклонение. Нормированная случайная величина. Начальные и центральные моменты. Асимметрия, эксцесс. Понятие о многомерных случайных величинах

Тема 10. Предельные теоремы.

Закон больших чисел. Неравенство Чебышева. Теорема Чебышева. Теорема Бернулли. Центральная предельная теорема. Теорема Ляпунова.