Из его средних групповых значений
| № группы | 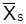 | 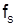 | 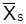 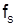 |
| 3946,67 | 11840,00 | ||
| 5250,00 | 26250,00 | ||
| 6845,00 | 47215,00 | ||
| 8499,00 | 84990,00 | ||
| 9826,00 | 29480,00 | ||
| 11750,00 | 23500,00 | ||
| Итого | – |
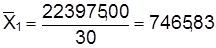 .
.
Таблица 15
Расчет дисперсии средней из групповых
| № группы | 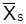 | 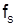 | 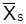 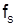 |
| 256355,56 | 769066,68 | ||
| 118000,00 | 590000,00 | ||
| 63750,00 | 446250,00 | ||
| 144729,00 | 1447290,00 | ||
| 70755,00 | 212265,00 | ||
| 62500,00 | 125000,00 | ||
| Итого | – | 3589871,68 |
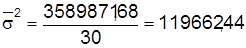 .
.
Таблица 16
Расчет межгрупповой дисперсии
| № группы | 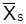 | 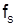 | 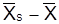 | 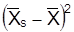 | 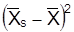 f f |
| 3946,67 | 3519,16 | 12384487,11 | 37153461,33 | ||
| 5250,00 | -2215,83 | 4909902,59 | 24549512,95 | ||
| 6845,00 | -620,83 | 385429,89 | 2698009,23 | ||
| 8499,00 | +1033,17 | 1067440,25 | 10674402,50 | ||
| 9826,67 | +2360,84 | 5573565,55 | 16720696,53 | ||
| 11750,00 | 4284,17 | 18354112,59 | 36708225,18 | ||
| Итого | – | – | 42674937,94 | 128504397,12 |
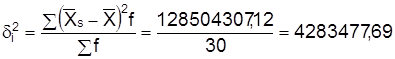 .
.
Расчет общей дисперсии по правилу сложения дисперсий:
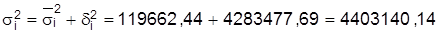 .
.
5. Расчет коэффициента детерминации и эмпирического корреляционного отношения:
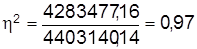
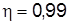 .
.
Аналогично проводятся расчеты для 2-го, 3-го и 4-го признака.
Выходная статистическая таблица результатов решения задачи 1,3 представляется следующим образом.
Таблица 17
Основные статистические характеристики
признаков Х1, Х2, Х3 и Х4
| № п/п | Статистические характеристики | Признаки | |||
| Х1 | Х2 | Х3 | Х4 | ||
| Общая средняя взвешенная величина | 7465,83 | 3663,00 | 3,73 | 0,50 | |
| Дисперсия средняя из групповых | 119662,44 | 205089,21 | 0,92 | 0,20 | |
| Межгрупповая дисперсия | 4283477,67 | 629753,45 | 0,39 | 0,06 | |
| Общая дисперсия | 4403140,14 | 834847,67 | 1,30 | 0,25 | |
| Коэффициент детерминации | 0,97 | 0,75 | 0,30 | 0,22 | |
| Эмпирическое корреляционное отношение | 0,99 | 0,87 | 0,55 | 0,47 |
Задача 1.5
По данным задачи 1.3 пункт 2 (выходные статистические табл. 2 и 3) рассчитайте средние значения признаков – Х1, Х2, Х3 и Х4 для всей совокупности данных как взвешанные среднегармонические величины.
Краткие методические указания к решению задачи 1.5.
При расчете величин применяются не только раннее проводимые простой и взвешанной средней арифметической величины, но и другие виды средних величин. Например, средняя гармоническая величина:
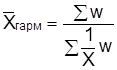 ,
,
где w – оборот; w = fx; 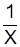 – обращенная варианта.
– обращенная варианта.
Именно этой формулой и следует воспользоваться при решении задачи 1.5.
Для признака Х1 имеем:
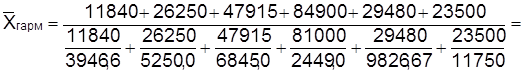
= 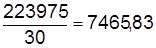 .
.
Аналогично для признаков Х2, Х3 и Х4. В результате получили средние значения признаков:
| Х1 | Х2 | Х3 | Х4 |
| 74465,83 | 3683,00 | 3,73 | 0,50 |
В нашей задаче средняя гармоническая – это расчетная форма средней арифметической, применении которой обусловлено характером имеющейся первичной информации.
Задача 1.6
Сопоставьте последовательно между собой частотное распределение единиц наблюдения по группам и структурные распределения совокупных обобщающих признаков – Х1, Х2 и Х3. Сопоставления произведите в двух вариантах – для групп с 10-ю и 20-ю процентной наполняемостью единицами наблюдения (выходные табл. 5 и 5а задача 1.3) Постройте графики Лоренца и рассчитайте коэффициенты Джини.
