Модификация метода ЧДЦ для сравнения проектов с разными сроками функционирования
В практике анализа инвестиционных проектов находят применение два подхода к выбору проектов с неравными сроками: метод продолженного срока и метод эквивалентного ежегодного аннуитета.
Метод продолженного срока предполагает возможность повторного осуществления проектов и использование критерия выбора ЧДД(по наибольшему значению) для многоразового осуществления проектов.
Рассмотрим проекты А1 и А2 с неравными сроками функционирования (табл. 7.6).
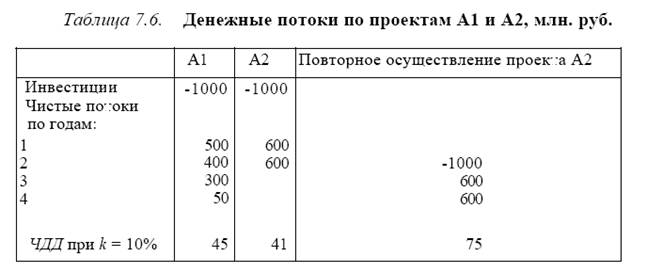
ЧДД проекта А1 больше, чем проекта А2, но выбор проекта А2 дает возможность осуществить еще один проект за рассматриваемый временной промежуток осуществления проекта А1. Двухразовое осуществление проекта А2 дает большее значение ЧДД. Следовательно, проект А2 предпочтительнее (предполагается возможность двухразового осуществления проекта при неизменной стоимости капитала, инвестициях и отдаче).
Метод продолженного срока предполагает:
1) нахождение наименьшего общего кратного для числа лет функционирования двух или нескольких оцениваемых проектов (например, при выборе из двух альтернативных проектов, рассчитанных на 2 и 3 года, продолженный срок функционирования равен 6 годам, один проект осуществится по данному методу два раза, а другой три раза);
2) расчет ЧДД многоразового осуществления каждого проекта на продолженном сроке NPV (i, n), где i — срок функционирования проекта, п — число осуществлений проекта, продолженный срок равен произведению in;
3) выбор проекта с наибольшим значением ЧДД.
Например, рассматриваются проекты С1 и С2 с равными инвестиционными затратами в году t = 0 и чистыми денежными потоками, представленными на рис. 7.5.
При стоимости капитала проекта 15% ЧДД по первому проекту (С1 с 3-летним сроком функционирования) равен 19,93. ЧДД проекта С2 = 6,7. Для сравнения проектов и выбора наилучшего следует найти продолженный срок для двух проектов. Срок функционирования первого проекта обозначим через i (i = 3), а второго j (j = 2). Наименьшее кратное равно 6 — это продолженный срок. Денежные потоки по проектам с учетом повтора изображены на рис. 7.6. Двухразовое осуществление первого проекта (n1 = 2) дает значение ЧДД, равное 33.
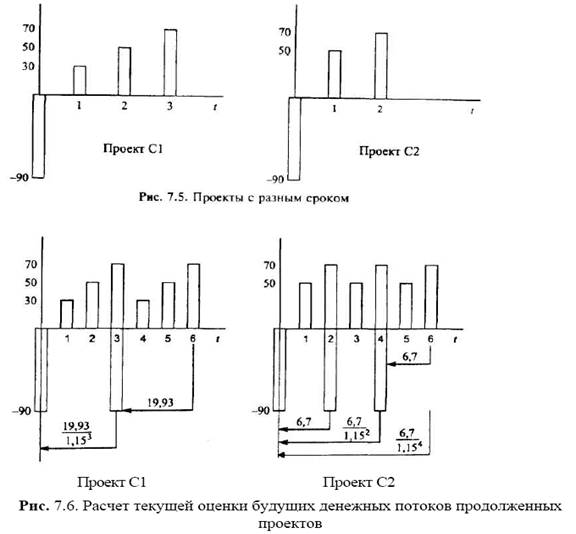
По второму проекту ЧДД для продолженного срока равен NPV(j, n2) = = NPV(2, 3) = 6,7 + 6,7/ 1,151х2 + 6,7/ 1,152х2= 15,6.
В общем случае
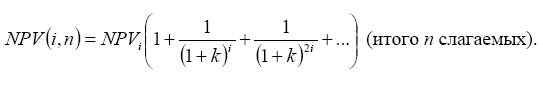
При большом числе слагаемых в формуле NPV(i, n), особенно если сравнивается много проектов, расчет может быть упрощен введением предположения о возможности неограниченного числа раз реализации проектов (n по всем ∞ → проектам). Предельное значение ЧДД по каждому проекту на продолженном сроке функционирования может быть найдено по формуле
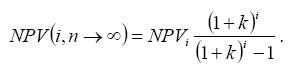
Например, по проектам С1 и С2 ]
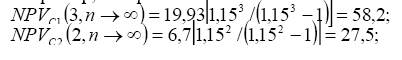
Проект С1 предпочтительнее.
Метод эквивалентного ежегодного аннуитета предполагает:
1) расчет ЧДД (NPV) по каждому проекту с индивидуальным сроком функционирования (NPVi);
2) нахождение денежного потока в виде аннуитета, который на индивидуальном сроке функционирования / обеспечивал бы то же значение ЧДД. Правило метода — проект с более высоким эквивалентным аннуитетом для любого срока функционирования обеспечит более высокое значение ЧДД, и такой проект предпочтительнее;
3) анализ может быть продолжен расчетом ЧДД по каждому проекту для бесконечного аннуитета. Если X— чистый денежный поток по аннуитету (возникает через равные промежутки времени в неизменном количестве), то ЧДД бессрочного аннуитета равен Х/k, где k — стоимость капитала. Правило метода — наибольшее значение ЧДД для бессрочного аннуитета характеризует лучший проект.
Рассмотрим использование метода для проектов А1 и А2, рассчитанных соответственно на 4 и 2 года (см. табл. 7.7 и рис. 7.7).

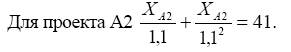
При стоимости капитала 10% аннуитет проекта А2 равен 23,63 (Л^ = 23,63). Аннуитет проекта А1 равен 14,2 (=45).
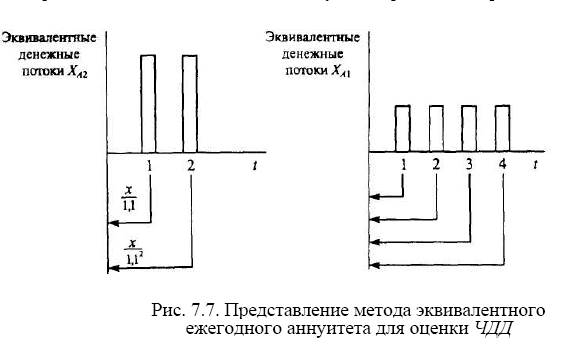
По правилу наибольшего значения аннуитета проект А2 предпочтительнее. В этом можно убедиться, рассчитав и ЧДД бесконечного аннуитета. ЧДД проекта А2 составляет 23,63/ 0,1 = 236,3. ЧДД проекта А1 - 14,2 /0,1 =142.
Рассмотренные два метода имеют ограничения:
1) если учесть инфляцию, то может оказаться, что повторное осуществление проекта обойдется дороже, чем прогнозируется при одноразовом осуществлении;
2) для проектов с длительным функционированием реально спрогнозировать срок довольно сложно и возможны погрешности. При большом значении наименьшего кратного и множестве проектов расчеты сильно усложняются. На практике, если рассматриваются, например, проекты со сроком функционирования 11 и 7 лет, которые имеют стандартные денежные потоки, то ограничиваются расчетом ЧДД для 7 лет или сравнением аннуитетов.
