Модели оценки обыкновенных акций

Особенность применения метода дисконтированных денежных потоков (ДДП) к оценке акции обусловлена составным характером денежного потока. Денежный поток по акции года (включает дивиденд на акцию за год) и прирост капитала, как разность между ценой продажи и ценой покупки. Акция в отличие от облигации дает право управления корпорацией, и теоретически размер дивиденда зависит от решений инвестора (обладание контрольным пакетом акций позволяет принимать решения о величине дивидендов и тем самым влиять на цену акции). Поэтому модели оценки акции не контрольного и контрольного пакетов должны отличаться. Подробно модели оценки совокупности акций рассматриваются в разделе II.

Общий подход ДДП используется при построении ряда моделей оценки акции, различающихся: 1) предположениями о закономерностях роста денежных потоков (постоянные потоки, постоянный рост, выделение различных фаз роста); 2) исходными параметрами для расчета денежного потока (дивиденд, чистая прибыль и дивидендный выход, операционная прибыль, чистый денежный поток).

Различные модели, предполагающие учет особенностей роста, будут рассмотрены на примере денежного потока — дивиденда на акцию.

Модель дисконтированных дивидендов с одной фазой роста

Для инвестора, принимающего решение об инвестировании денежных средств в покупку акции, будущие денежные потоки являются потоками дивидендов и прироста капитала при продаже акции. С точки зрения неперсонифицированного инвестора частота продаж не влияет на текущую оценку. Эта оценка определяется перспективами получения владельцем акции денежных поступлений, т.е. зарабатыванием корпорацией чистой прибыли. Так как период обращения акции не ограничен, то обезличенный инвестор будет на протяжении всего срока обращения рассчитывать только на получение дивидендов, и текущая оценка акции Р0 будет равна сумме дисконтированных потоков дивидендов на бесконечном временном горизонте:

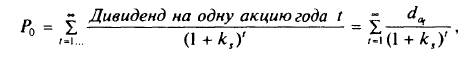
где к5 — требуемая инвесторами доходность.

Если дивиденд не изменяется по годам

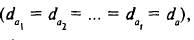
то

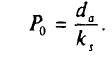
При постоянстве денежных потоков на бессрочном временном горизонте оценка актива есть отношение фиксированного денежного потока к доходности актива (ожидаемой и требуемой). Вывод этого уравнения показан в Приложении 1 ("Будущая и текущая оценки аннуитета").

Если ожидается рост дивидендов с постоянным темпом, т.е. da1 = dt-1 (1 + g), то цена акции определяется фиксированным размером дивиденда будущего года da1, темпом роста g и требуемой доходностью акционеров с учетом риска (модель бессрочного роста Гордона).

Формула оценки акции Гордона (вывод см. в Приложении 1 "Текущая оценка неравных денежных потоков"):

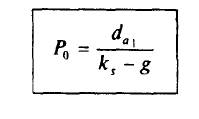
Модель Гордона для оценки акции по текущему дивиденду:

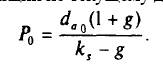
Эта модель лучше всего прогнозирует цену акции корпораций, темп роста которых равен или ниже номинального роста экономики или отрасли, имеющих постоянный дивидендный выход и стабильную дивидендную политику. Например, если для США номинальный рост экономики составлял в 1993 г. 6% (4% — инфляция и 2% — реальный рост), то модель Гордона может быть применена к корпорациям со стабильным темпом роста, не превышающим 6%.

?Может ли в модели Гордона рассматриваться падение дивидендных выплат? Как следует модифицировать модель при рассмотрении реального темпа роста?

Аналогичным образом при постоянстве дивидендного выхода текущая оценка цены Р0 может быть рассчитана через поток чистой прибыли, ожидаемый в будущем году. Da1 N / πa = ψ — дивидендный выход, N — число акций в обращении, πа — чистая прибыль на акцию (ЕРS), дивиденд будущего года может быть выражен через ожидаемое значение чистой прибыли на акцию и стабильное значение дивидендного выхода:

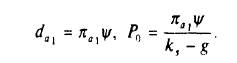
Например, корпорация ХУZ в 1995 г. обеспечила значение прибыли на акцию 6,8 долл. Корпорация придерживается политики постоянного дивидендного выхода 55%. В период 1989—1995 гг. чистая прибыль росла с темпом 4%. Предположение о стабильном росте позволяет получить прогноз цены акции на 1996 г. Используя данные о номинальной ставке процента по долгосрочным государственным облигациям (7%) и премии за риск инвестирования в данную корпорацию (3%), получаем требуемую инвесторами доходность kS = 10%. Р1996 = πa1995 ψ (1 +g) / (kS - g) = 6,8 х 0,55 х 1,04) / (0,1 - 0,04) = 64,83 долл.

?Аналитики, исходя из прошлого роста и монопольных позиций на рынке компании "Майкрософт" (Microsoft Corp), рыночная капитализация которой на 1997 г. составила 159,66 млрд. долл. (конец сентября 1997 г. по рейтингу ФТ-500), прогнозируют 15%-й ежегодный прирост прибыли компании. Объясните, почему такой прогноз неверен.

Многофазовые модели роста

Многофазовые модели роста предполагают, что во временном разрезе дивидендных потоков существуют определенные закономерности роста.

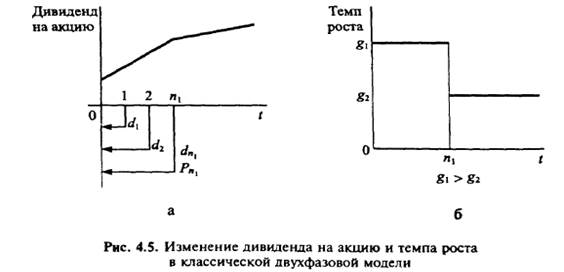
1. Двухфазовая модель ростапредполагает, что для корпорации можно выделить две фазы развития, для которых характерен стабильный рост дивидендов (или иных определяющих параметров. В первой фазе для корпорации характерен быстрый (экстраординарный) рост дивидендов, затем на второй фазе возможности роста снижаются и приближаются к темпам роста экономики в целом (рис. 4.5).

Факторы, влияющие на модель:

• темп роста в первый период — чем выше экстраординарный рост, тем выше оценка акции;

• длительность первого периода — чем длиннее первый период экстраординарного роста, тем выше оценка акции;

• рентабельность деятельности — оказывает влияние на темп роста и оценку;

• риск, выражаемый в ставке дисконтирования k.

При предположении о продолжительности первой фазы в n1, лет (темп роста дивидендов g,), а затем бессрочном росте с темпом g2 текущая оценка акции (равновесная цена) может быть записана как

Р0 = Сумма дисконтированных дивидендов за n1 лет + Оценка акции на конец года n1, приведенная к начальному году.

Первая фаза роста может быть представлена растущим аннуитетом на отрезке n1 лет (см. в Приложении 1 "Текущая оценка неравных денежных потоков"), вторая фаза — бессрочным растущим аннуитетом, текущая оценка которого может быть найдена по модели Гордона. Оценка акции по двухфазовой модели:

РV= Растущий аннуитет на отрезке n1 лет + РV оценки акции на конец года n1

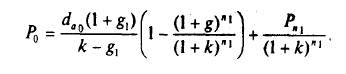
Pn1 = da(n1 +1) / (k – g) по модели бессрочного роста Гордона. Дивиденд на акцию в году t = n1 + 1 можно выразить следующим образом: da(n1 + 1) = da n1 x (1 + g2)n1 (1 + g2).

Теперь выражение цены акции (текущей оценки) примет вид

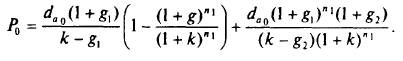
Факторы, определяющие темп роста дивиденда на акцию:

доходность (рентабельность) активов корпорации RОА, как отношение чистой прибыли данного года к среднегодовой величине активов;

дивидендный выход ψ, как отношение суммы, направляемой на выплату дивидендов, к величине чистой прибыли;

соотношение между заемным и собственным капиталом D/S (например, балансовые оценки);

величина процентов по заемному капиталу, как отношение выплат в течение года по заемному капиталу к величине заемного капитала i (в %);

ставка налога на прибыль.

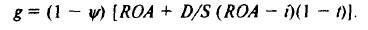
Например, если по корпорации на основе балансовой отчетности рассчитаны: доходность активов КОА =12%, дивидендный выход в течение прошлых лет у = 60%, величина заемного капитала равна величине собственного (D/S = 1), i = 10%, t = 40%, то g = (1 - 0,6) х [12% + 1 х (12% - 10%) х (1 - 0,4)] = 7,2 %.

К недостаткам двухфазовой модели роста относится то, что она исходит из предпосылки, что на первой фазе корпорация имела конкурентные преимущества, которые потеряны на конец года пг Например, закончился срок лицензии или права использования того или иного ресурса, что повлекло снижение роста. Причиной высокого роста на первой фазе может быть значительный спрос на новый продукт или легализация ранее запрещенного вида деятельности. Все описанные возможные варианты объяснения высокого роста на первой фазе, естественно, должны исходить из различной оценки риска на первой и второй фазах, что должно найти отражение в введении различных ставок дисконтирования: k1 и k2.

?Какие предположения о ставках дисконтирования могут быть сделаны? Какие факторы должны быть приняты во внимание?

Оценка акции по двухфазовой модели может быть разложена на иные компоненты: не во временном аспекте, а по премиям к оценке неизменных выплат. Идея такого разложения заключается в понимании того, что оценка акции с высоким ростом на первой фазе должна быть выше, чем цена акции по однофазовой модели стабильного роста (по модели Гордона). В свою очередь, оценка акции, которая соответствует предположениям модели Гордона, выше, чем оценка акции со стабильными выплатами по годам. Таким образом, цена акции с двумя фазами роста складывается из оценки неизменных потоков, премии за стабильный рост и премии за экстраординарный рост на первой фазе:

2. Трехфазовая модель.Модель предполагает три фазы дивидендных выплат:

фаза 1 — фаза высокого роста, темп роста равен gа на отрезке времени

фаза 2 — переходная фаза, период снижения роста, конкурентные преимущества высокого роста потеряны;

фаза 3 — фаза стабильного роста, темп роста равен gп.

Фазы дивидендных выплат соответствуют жизненному циклу продукции и стадиям развития компании. Естественно предположить, что переход из одной стадии в другую меняет дивидендную политику, поэтому дивиденд на акцию на каждой стадии должен рассчитываться обособленно (см рис 4 6 и табл. 4.4).

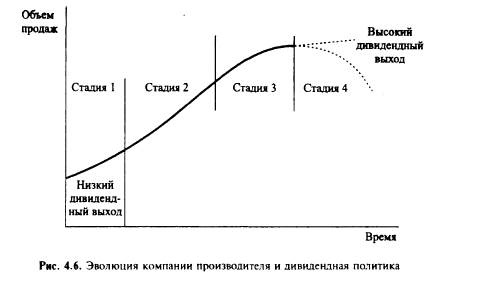
Например, введение дивидендного выхода на фазе 1 — V, и на фазе 2 — у2 и прибыли на акцию для года I = 0 ;га и года ( = п па позволяет оценить дивиденд на акцию на начальные годы каждой фазы: при / = 0 — йа = па V,, при t = п dan = πan ψ2.

Взаимосвязь темпа роста прибыли и дивидендного выхода в трехфазовой модели показана на рис. 4.7.

Модель рекомендуется использовать при высоких значениях роста на первой фазе (выше 25%) и стабильном росте на третьей фазе (4—8% в год).

Например, рассмотрим оценку корпорации Соса-Со1а, развитие которой в наилучшей степени может быть описано трехфазовой моделью. В 1993 г. корпорация объявила прибыль на акцию за 1992 г. в размере 1,43 долл. и дивиденд на акцию в размере 0,56 долл. В предыдущие годы (оценка за 5 лет) прибыль на акцию росла с темпом 18% в год, и проведение агрессивной политики расширения рынков сбыта в зарубежных странах позволило аналитикам прогнозировать темп роста выручки (реализационного дохода) в 17% на ближайшие 5 лет.

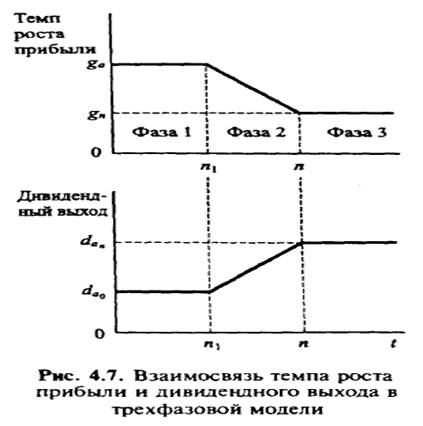
Высокая доходность активов (ИОЛ = 29,3%) в сочетании с высокой долей нераспределенной прибыли в зарабатываемой чистой прибыли (60%) обеспечивали до 1992 г. высокий рост (26,02%). Корпорация намеревалась поддерживать темп роста прибыли на уровне 19,44% в год на период 1993—1997 гг. На следующие 5 лет аналитики предвидели переходную фазу, когда возможности расширения будут исчерпаны и произойдет переход на стабильный рост прибыли, сравнимый с ростом экономики США (6% годовых).

На второй фазе развития снизится риск и возрастет значение дивидендного выхода с 40 до 78,81%.

Оценка акции складывается из текущих оценок на всех трех фазах.

3. Многофазовые модели роста и Н-модель.Часто предположения об изменении дивидендных выплат усложняются введением множества точек изменения, когда значения темпа роста скачкообразно меняются от одного значения до другого.

Например, на отрезке времени Х1 сохраняется темп роста дивиденда g1 на отрезке X2 — темп роста g2 на отрезке Х3 — g3 и так далее до нормального темпа роста gn. Графически изменение темпа роста во времени показано на рис.4. 8а.

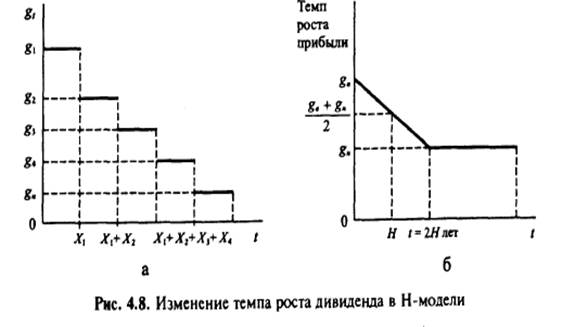
Оценка акции в такой многошаговой модели может быть аппромиксирована следующим выражением:

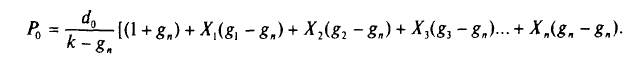
Х{, Хг Х} и т.д. показывают продолжительность во времени каждого шага.

Если рассматривается трехшаговая модель, то вводится только три значения темпа роста g1, g2 и нормальный темп gп. Продолжительность первого шага — Х1 продолжительность второго шага — Х2 и в момент времени В = Х1 + Х2 темп роста дивидендов скачкообразно достигнет значения gл. Предположив, что темп роста второго шага g2 определяется из соотношения (g1+gn)/ 2, при подстановке в формулу оценки цены многошаговой модели получаем

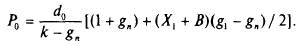
Заменив (Х1+В)/2 на H, получаем Н-модель, предложенную в 1984 г. Р.Фулером и К. Шиа.

Оценка акций по Н-модели:

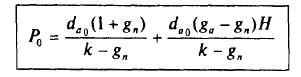
Как видно из формулы, при равенстве ga и gn получаем модель постоянного роста Гордона.

Предположения модели:

• в год t/ = 0 темп прироста дивиденда на акцию равен ga (высокий начальный уровень);

• темп роста линейно снижается в течение 2Н лет;

C начала года (2Н + 1) темп роста постоянен и совпадает с темпом роста экономики (или отрасли) в целом. Нормальный ежегодный темп роста - gn;

•дивидендный выход постоянен по всем годам модели (рис 4.8б)

H - модель наиболее приемлема для корпораций, которые росли до настоящего момента очень быстро, но к моменту t=0 достигли большого размера, и темп их роста замедляется. Допущение о постоянном дивидендном выходе мало согласуется с традиционными подходами к выплате дивидендов, но может быть применено к корпорациям, которые придерживаются политики низких дивидендов или вообще их не платят.

Например, корпорация "Атон" (производитель лекарственных препаратов) в 1998 г. заработала чистую прибыль на акцию в размере 2,55 долл. и выплатила дивиденд на акцию в размере 1,1 долл. (за 1998 г.). В предыдущие 5 лет прибыли росли на 18 % в год, но эксперты предсказывают снижение темпов под действием трех факторов: а) снижения прибыльности основного продукта корпорации из-за возрастания конкуренции, в том числе роста импорта, б) снижения прибыльности всей отрасли, в) роста размера корпорации и усложнения управления. Предполагается снижение на 2,33% в год в течение 6 лет до достижения стабильного темпа роста 4% годовых.

Применим Н-модель. Ставка дисконтирования k может быть оценена по модели оценки долгосрочных активов (САРМ) на уровне 14%. da0 = 1,1, 2Н = 6 лет, ga = = 18%, gn = 4%, k = 14%. P0 = 1,1 х (1 + 0,04) х (0,14 - 0,04) + 1,1 х (0,18 - 0,04) х х(6/2) / (0,14 - 0,04) = 16,06 долл.