Методы теории принятия решений
Задачи линейного программирования
Транспортная задача является наиболее известной из всех задач линейного программирования. В общем виде она заключается в следующем: имеется m поставщиков и n потребителей. Если возможности поставщиков ai (i=1, …, m); количество продукции, необходимой потребителям bj (j=1, …, n), размеры поставок от поставщика i к потребителю j - Xij; затраты на перевозку единицы продукции из пункта i в пункт j - Cij, то транспортная задача линейного программирования представляется следующим образом:
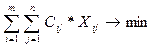 (36)
(36)
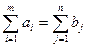 (37)
(37)
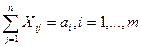 (38)
(38)
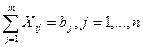 (39)
(39)
Сij, Xij ≥ 0 (40)
Первое ограничение означает, что общее количество продукции, необходимой всем потребителям, должно соответствовать общему ее количеству, находящемуся у поставщиков (так называемая закрытая транспортная задача). Второе и третье ограничения задача требуют, чтобы вся продукция каждого поставщика была распределена и заявки всех потребителей были полностью удовлетворены.
Задача 37
Определить размеры поставок ресурсов от поставщика к потребителю. Общие затраты на поставку всей продукции должны быть минимальными.
| Потребители Поставщики | В1 | В2 | В3 | В4 | В5 | Запасы |
| А1 | 10 | 7 | 4 | 1 | 4 | |
| А2 | 2 | 7 | 10 | 6 | 11 | |
| А3 | 8 | 5 | 3 | 2 | 2 | |
| А4 | 11 | 8 | 12 | 16 | 13 | |
| Потребности |
Задача 38
Составить план выпуска продукции (оконные рамы), при котором предприятие получит максимальную прибыль. Решение определить графически и с помощью системы уравнений.
| Цех | Продукция | Максимально возможная загрузка в неделю | |
| А | В | ||
| 1. Сборочный 2. Отделочный | 2 ч/шт. 3 ч/шт. | 4 ч/шт. 2 ч/шт. | |
| Валовая прибыль | 10 тыс.руб./шт. | 17 тыс.руб./шт. |
Анализ чувствительности
Анализ чувствительности является одним из простейших и наиболее распространенных методов анализа риска. С его помощью можно выяснить, какие именно факторы (оцениваемые параметры) можно отнести к наиболее рискованным.
Как показатель чувствительности объекта риска относительно изменения определенных факторов используются эластичность или чувствительность реагирования. Эластичность - мера реагирования одной переменной величины (функции) на смену другой (аргумента), а коэффициент эластичности - это число, которое показывает процентное изменение функции в результате процентного изменения аргумента.
Коэффициент эластичности (чувствительности) объекта риска относительно переменной хі, і=1,....,n, определяют по формуле:
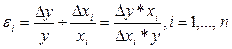 (41)
(41)
Метод анализа чувствительности на сегодняшний день чаще всего используется для анализа инвестиционных проектов - определение степени устойчивости проекта к влиянию внешней или внутренней среды.
В теории инвестиций такое влияние выражается через коэффициент дисконтирования. Эта задача сводится к тому, чтобы определить каким образом изменится значение NPV проекта при увеличении ставки дисконта, который выражает состояние макросреды.
Модель NPV в общем виде имеет следующий вид:
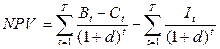 (42)
(42)
где: Bt - величина дохода в t-м периоде от реализации инвестиционного проекта; Ct - величина расходов в t-м периоде на реализацию инвестиционного проекта; It - сумма инвестиций в t-м периоде; d - ставка дисконта; t - значение определенного периода реализации инвестиционного проекта.
Эластичность NPV по коэффициенту дисконта, — относительное изменение NPV при изменении дисконта на 1 %.
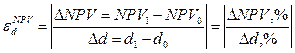 (43)
(43)
Для измерения процентного изменения величины спроса используется формула средней точки Алена:
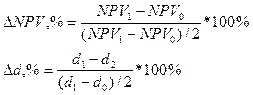 , (44)
, (44)
где NPV0,1 – NPV в базисном и отчетном периодах соответственно; d0,1 – коэффициент дисконта в базисом и отчетном периодах соответственно.
Задача 39
Срок реализации проекта составляет 3 года. Соответственно денежные потоки (Bt-Ct)прогнозируются в размере 500 тыс.д.е., 800 тыс. д.е., 700 тыс. д.е. Сумма инвестиций, которые вкладываются единовременно до начала реализации проекта, составляет 1000 тыс. д.е. Ставка дисконта для данного проекта определенна в размере 15 %.
Необходимо установить, какое влияние будет иметь на проект условия внешней среды, т.е. на сколько процентов изменится значение NPV, если ставка дисконта изменится на 1 % и составит 16%.
