Нахождение процентной ставки

1. Эффективная ставка процента

r_е=(1+ 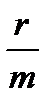)^m-1 (1.14)

Годовая ставка, обеспечивающая тот же доход, что m-разовое начисление по номинальной (годовой) ставке r называется эффективной ставкой, т.е.

(1+ r_e)^t = (1+ 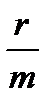)^m*t (1.15)

r_e> r (1.16)

Эффективная ставка представляет собой реальный, фактический доход (в процентах) от вклада, который получит инвестор, если проценты начисляются более чем 1 раз в год. Номинальная ставка (r) – это годовая процентная ставка, указанная в договоре при оформлении депозита или других операций. Эффективная годовая процентная ставка учитывает размер номинальной ставки в пределах периода начисления (номинальная периодическая ставка r/m и число периодов начисления m). При этом (1+r/m) – это денежный прирост по инструменту за один период начисления процентов, а степень m показывает частоту появления такой ситуации. Полученная годовая ставка процента называется эффективной, поскольку она обеспечит тот же самый доход, который был бы получен, если бы начисление осуществлялось один раз в год при ставке EAR.

2. Эквивалентная ставка сложных процентов находится по средней геометрической взвешенной:

r = -1 (1.17)

Необходимо обратить внимание на расчет средних значений эквивалентности ставок, так как для нескольких процентных ставок их среднее значение является эквивалентной величиной.

3. Когда необходимо рассчитать уровень процентной ставки для финансовых контрактов, то можно воспользоваться формулами (1) и (2), в случае начисления процентов по простой и сложной схеме.

3.1. Сумма процента за установленный период времени, рассчитанная по простым процентам:

I = PV*n*r (1.18)

где I – сумма процентов за установленный период времени.

3.2.Ставка сложных процентов:

r_слож = 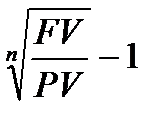(1.19)

где r_слож – ставка сложных процентов.

1.1.3. Нахождение текущей стоимости (дисконтированной) однократного вложения – (Present Value)

Настоящая (текущая) стоимость PV денег равна сегодняшней стоимости вложения, которое мы получим в будущем. Например, зная, какую сумму вы получите через год, можно сказать, какой сумме она эквивалента сегодня. Процесс определения PV называется дисконтированием. При этом расчет первоначальной стоимости отличается в зависимости от начисления простых или сложных процентов.

1. Величина первоначальной суммы начисленной по простым процентам:

PV = 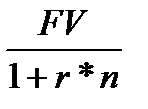(1.20)

2. Величина первоначальной суммы начисленной по сложным процентам:

PV = 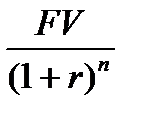(1.21)

Коэффициент 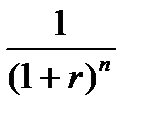называется коэффициентом дисконтирования.Он характеризует текущую стоимость денежной единицы полученной в будущем. Для нахождения этого коэффициента можно воспользоваться таблицей, приведенной в Приложении 2. Она дает оценку не приносящей доход денежной единицы, через заданный промежуток времени при фиксированном значении среднегодовой ставки банковского процента (можно использовать как норму дисконта, норму прибыли).

3. Сумма дисконта за определенный период времени:

D= FV-PV (1.22)

где D – сумма дисконта за определенный период времени.

4. Величина простой учетной ставки

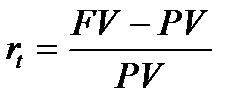-темп прироста денежной единицы (1.23)

где r_t – в финансовых вычислениях этот показатель называется «процентная ставка», «процент», «рост», «ставка процента», «норма прибыли».

d_t = 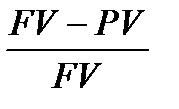– темп снижения денежной единицы (1.24)

где d_t – в финансовых вычислениях этот показатель называется «учетная ставка», «ставка дисконтирования» для конкретного периода.

взаимосвязь по сложным процентам

r_t = 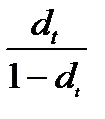(1.24) d_t = 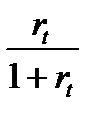(1.25)

т.е. r_t>d_t

взаимосвязь по простым процентам

r_t = 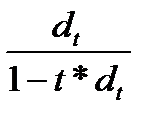(1.26) d_t = 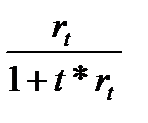(1.27)

5. Дисконтирование можно проводить m – раз в году:

PV = 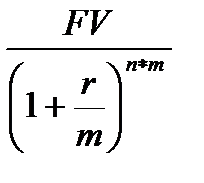(1.28)

6. Наращенная сумма, рассчитанная по сложной учетной ставке:

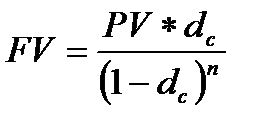(1.29)

7. Наращение суммы возможно путем капитализации процентов несколько раз в году или по годовой (номинальной) учетной ставке:

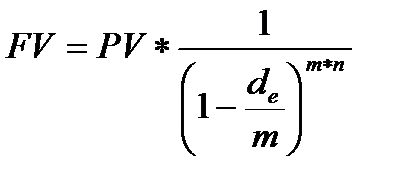(1.30)

Тот же результат может быть получен при использовании эффективной учетной ставки. Под эффективной учетной ставкой понимают сложную годовую учетную ставку, эквивалентную номинальной учетной ставке при заданном значении m. Эффективная учетная ставка меньше эквивалентной.

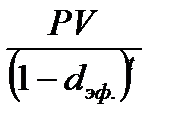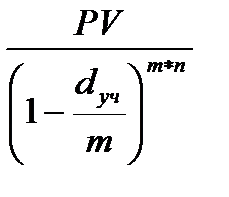= (1.31)

d_эф = 1– (1– 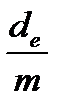)^m (1.31)

d_эф< d_е

При дисконтировании m раз в году используются номинальная учетная ставка. Расчет дисконтированной величины производится по формуле:

PV *d_е = FV * (1– 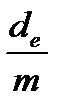)^n*m (1.32)

где d_e – учетная ставка в операциях по учету векселей и когда берется кредит.

8. При банковском дисконтировании приведенная стоимость к текущему моменту для учета векселей определяется по формуле:

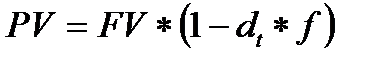(1.33)

где FV – номинальная стоимость векселя;

PV –дисконтная (учетная) стоимость векселя;

d_t – банковская учетная ставка;

f – относительная длина периода до погашения ссуды.

Вексель размещается и реализуется, как правило, с дисконтом, поэтому абсолютный доход определяется разностью его номинальной и дисконтной ценой. Если вексель размещается по номиналу, то абсолютный размер дохода векселедержателя определяется процентной ставкой.

9. Сумма гашения (учета) векселя с помощью математического метода, то есть по процентной ставке r делается по формуле:

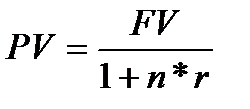(1.34)

Сумма гашения (учета) векселя банковским методом с помощью учетной ставки – de производится таким образом:

10. a) по формуле простых процентов:

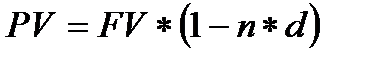(1.35)

b) по формуле сложных процентов

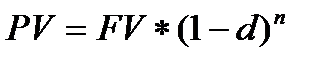(1.36)

где FV – номинальная стоимость векселя;

PV – сумма векселя к оплате.

Дисконтирование с помощью банковского и математического методов дают разные финансовые результаты.

11. Если расчеты делаются по периодам:

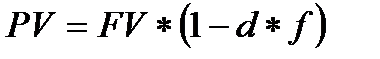(1.37)

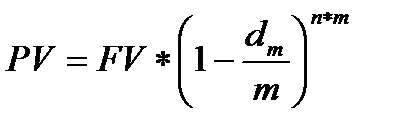(1.38)

где n – количество лет;

m – количество периодов начисления внутри года;

f – дробная часть года.