Результативные таблицы и графики

Таблица 1 – Исходные данные
Номер предприятия	Среднегодовая стоимость основных производственных фондов, млн.руб.	Выпуск продукции, млн. руб.
	1232,00	1184,50
	1450,50	1299,50
	1496,50	1449,00
	1577,00	1610,00
	1025,00	805,00
	1657,50	1380,00
	1703,50	1863,00
	1278,00	1265,00
	1565,50	1483,50
	1807,00	1851,50
	1979,50	1955,00
	1508,00	1541,00
	1657,50	1679,00
	1899,00	2035,50
	2175,00	2185,00
	1623,00	1472,00
	1795,50	1748,00
	1427,50	1092,50
	1818,50	1495,00
	2025,50	2012,50
	1393,00	1138,50
	1105,50	1069,50
	1853,00	1713,50
	1657,50	1495,00
	1542,50	1414,50
	1197,50	920,00
	1611,50	1437,50
	1864,50	1575,50
	1772,50	1495,00
	1301,00	1334,00

Таблица 2 – Аномальные единицы наблюдения
Номер предприятия	Среднегодовая стоимость основных производственных фондов, млн.руб.	Выпуск продукции, млн. руб.
	680,00	1725,00
	2175,00	575,00

Таблица 3 – Описательные статистики
По столбцу «Среднегодовая стоимость основных производственных фондов, млн.руб.»	По столбцу «Выпуск продукции, млн.руб»
Столбец1		Столбец2
Среднее	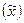	Среднее	1499,983333
Стандартная ошибка	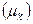50,78412165	Стандартная ошибка	60,58109642
Медиана	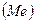1617,25	Медиана	1489,25
Мода	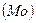1657,5	Мода
Стандартное отклонение	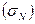278,1560899	Стандартное отклонение	331,8163307
Дисперсия выборки	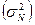77370,81034	Дисперсия выборки	110102,0773
Эксцесс	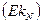-0,34494384	Эксцесс	-0,20533236
Асимметричность	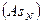-0,15250365	Асимметричность	0,04295445
Интервал	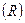	Интервал
Минимум		Минимум
Максимум		Максимум
Сумма		Сумма	44999,5
Счет		Счет
Уровень надежности(95,4%)	105,8753446	Уровень надежности(95,4%)	126,3001948

Таблица 4а – Предельные ошибки выборки
По столбцу «Среднегодовая стоимость основных производственных фондов, млн.руб.»	По столбцу «Выпуск продукции, млн.руб»
Столбец1		Столбец2
Уровень надежности(68,3%)	51,70867028	Уровень надежности(68,3%)	61,68400355
Таблица 4б – Предельные ошибки выборки
По столбцу «Среднегодовая стоимость основных производственных фондов, млн.руб.»	По столбцу «Выпуск продукции, млн.руб»
Столбец1		Столбец2
Уровень надежности(99,7%)	164,5101776	Уровень надежности(99,7%)	196,2465158

Таблица 5 – Выборочные показатели вариации и асимметрии
По столбцу «Среднегодовая стоимость основных производственных фондов, млн.руб.»	По столбцу «Выпуск продукции, млн.руб»
Стандартное отклонение	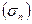273,481	Стандартное отклонение	326,239
Дисперсия	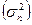74791,783	Дисперсия	106432,008
Среднее линейное отклонение	220,033	Среднее линейное отклонение	251,313
Коэффициент вариации, %	17,093	Коэффициент вариации, %	21,750
Коэффициент асимметрии	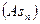-0,210	Коэффициент асимметрии	0,015

Таблица 6 – Расчет нижних и верхних границ интервалов
Карман	Частота

Таблица 7 – Интервальный ряд распределения предприятий по стоимости основных производственных фондов
Карман	Частота	Интегральный %
1025		0
		13,33%
		30,00%
		66,67%
		90,00%
		100,00%
		100,00%

Таблица 7а – Распределение предприятий по стоимости основных производственных фондов
Группы предприятий по среднегодовой стоимости основных фондов, млн. руб.	Число предприятий в группе	Накопленная частость группы, %
Ед.	В % к итогу
1025-1255		13,3%	13,33%
1255-1485		16,7%	30,00%
1485-1715		36,7%	66,67%
1715-1945		23,3%	90,00%
1945-2175		10,0%	100,00%
Итого		100,0%

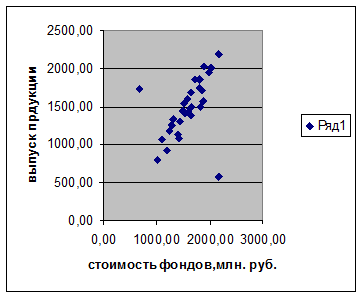
Рис. 1. Аномальные значения признаков на диаграмме рассеяния

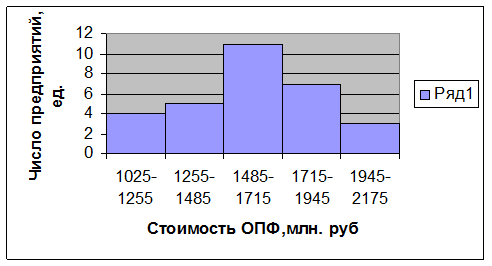
Рис. 2. Гистограмма распределения единиц совокупности по признаку среднегодовая стоимость основных производственных фондов

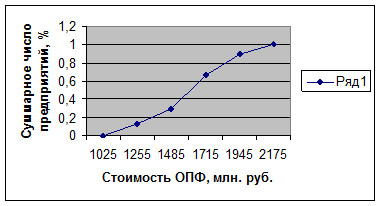
Рис. 3. Кумулятивное число единиц совокупности по признаку среднегодовая стоимость основных производственных фондов

СТАТИСТИЧЕСКИЙ АНАЛИЗ ВЫБОРОЧНОЙ СОВОКУПНОСТИ

Задача 1

Выявление аномальных значений признака наиболее удобно производить графическим методом. По расположению точек на точечном графике можно выявить значения признака, которые резко выделяются из общей однородной массы значений признаков единиц совокупности (Рис. 1). В результате было выявлено, что 12 и 31 предприятия являются аномальными значениями признаков (Таблица 2). Дальнейшее исследование совокупности проводиться без учета аномальных единиц наблюдения (Таблица 1).

Задача 2

Таблица 8 – Описательные статистики выборочной совокупности

По столбцу «Среднегодовая стоимость основных производственных фондов, млн.руб.»	По столбцу «Выпуск продукции, млн.руб»
Столбец1		Столбец2
Среднее		Среднее	1499,983333
Медиана	1617,25	Медиана	1489,25
Мода	1657,5	Мода
Интервал		Интервал
Стандартное отклонение	273,481	Стандартное отклонение	326,239
Дисперсия	74791,783	Дисперсия	106432,008
Среднее линейное отклонение	220,033	Среднее линейное отклонение	251,313
Коэффициент вариации, %	17,093	Коэффициент вариации, %	21,750
Коэффициент асимметрии	-0,210	Коэффициент асимметрии	0,015

Столбец «Среднегодовая стоимость ОПФ, млн. руб.»(аналогично столбец «Выпуск продукции»):

Среднее значение: среднегодовая стоимость ОПФ по 32 предприятиям равняется 1600 млн. руб.

Медиана: 50% предприятий имеют среднегодовую стоимость ОПФ меньше 1617,25 млн. руб., остальные 50% более 1617,25 млн. руб.

Мода: в данной совокупности предприятий наиболее часто встречается среднегодовая стоимость ОПФ 1657,5 млн. руб.

Интервал – размах вариации (R = хmaх – хmin) – устанавливает предельное значение амплитуды колебаний признака, в выборке равен 1150.

Стандартное отклонение показывает на сколько в среднем отклоняются конкретные варианты от их среднего значения. В среднем среднегодовая стоимость ОПФ каждого предприятия отклоняется от среднего значения примерно на 273,48 млн. руб.

Дисперсия: оценивает средний квадрат отклонений.

Среднее линейное отклонение – среднее арифметическое из абсолютных значений отклонений отдельных вариантов от их средней арифметической.

Коэффициент вариации оценивает интенсивность колебаний вариантов относительно их средней величины.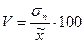

Vσ = 17,093 % (Vσ ≤ 40%): вариация признака незначительная, совокупность количественно однородна, среднее значение типичное и надежное.

Коэффициент асимметрии Пирсона: оценивает смещение ряда распределения влево или вправо по отношению к оси симметрии нормального распределения.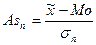

As = -0,21 (|As| ≤ 0,25), следовательно, асимметрия левосторонняя незначительная; распределение близко к нормальному. Среди предприятий в выборке чаще встречается размер среднегодовой стоимости ОПФ больший, чем среднее значение – 1600 млн. руб.

Задача 3

а) степень колеблемости значений признаков в совокупности:

Коэффициент вариации (Vσ) признака «среднегодовая стоимость основных производственных фондов» равен примерно 17,093 %: степень колеблемости значений признаков в совокупности относительно средней величины незначительная (Vσ ≤ 40%), среднее значение типичное и надежное.

Коэффициент вариации (Vσ) признака «выпуск продукции» равен примерно 21,75 %: степень колеблемости значений признаков в совокупности относительно средней величины незначительная (Vσ ≤ 40%), среднее значение типичное и надежное.

Б) степень однородности совокупности по изучаемым признакам:

Коэффициент вариации служит индикатором однородности совокупности: если он меньше 33%, то совокупность является количественно однородной по данному признаку. 17,093 % ≤ 33 %, 21,75 % ≤ 33 % - данные совокупности количественно однородны.

В) устойчивость индивидуальных значений признаков:

Отношение показателей 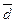и σ может служить индикатором устойчивости данных, если .

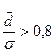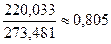, следовательно, значения признака «среднегодовая стоимость основных производственных фондов» неустойчивы, в них имеются «аномальные» выбросы.

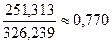, следовательно, значения признака устойчивы, в них нет «аномальных» выбросов.

г) Согласно правилу «трех сигм», в нормально распределенных и близких к ним рядам, ожидаемое процентное соотношение рассеяния значений признака по трем диапазонам: 68,3 % - в диапазоне 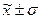; 95,4% - в диапазоне 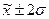; 99,7 % - в диапазоне 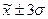. В исследуемой совокупности процентное соотношение рассеяния значений признака по трем диапазонам приближенно соответствует правилу «трех сигм» (таблица 10).

Таблица 9 – Распределение значений признака по диапазонам рассеяния признака относительно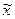

	Границы диапазонов	Количество значений 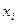, находящихся в диапазоне
	Среднегодовая стоимость ОПФ	Выпуск продукции	Среднегодовая стоимость ОПФ	Выпуск продукции
Ед.	%	Ед.	%
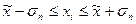	1326,52 ≤ 1600 ≤ 1873,48	1173,74 ≤ 499,98 ≤ 1826,22		66,7%		63,3%
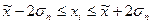	1053,04 ≤ 1600 ≤ 2146,96	847,5 ≤ 1499,98 ≤ 2152,46		93,3%		93,3%
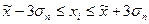	779,56 ≤ 1600 ≤ 2420,44	512,26 ≤1499,98 ≤ 2478,7		100%		100%

Вывод: 66,7% значений среднегодовой стоимости ОПФ находятся в пределах от 1326,52 млн. руб. до 1873,48 млн. руб.;

93,3 % значений среднегодовой стоимости ОПФ находятся в пределах от 1053,04 млн. руб. до 2146,96 млн. руб.;

100% значений среднегодовой стоимости ОПФ находятся в пределах от 779,56 млн. руб. до 2420,44 млн. руб.

63,3% значений выпуска продукции находятся в пределах от 1773,74 млн. руб. до 1826,22 млн. руб.;

93,3% значений выпуска продукции находятся в пределах от 847,5 млн. руб. до 2152,46 млн. руб.;

100% значений выпуска продукции находятся в пределах от 512,26 млн. руб. до 2478,7 млн. руб.;

Задача 4

а) вариации признаков:

Коэффициент вариации признака «среднегодовая стоимость ОПФ» равен 17,093 %, а признака «выпуск продукции» - 21,75 %; из этого следует, что совокупность по признаку «среднегодовая стоимость ОПФ» более однородна, чем по второму, так как чем больше величина коэффициента вариации, тем больше разброс значений признака вокруг средней. Колеблимость признаков в обоих рядах распределения незначительная.

б) признаки в обоих рядах распределения количественно однородны.

в) надежности (типичности) средних значений признаков:

Коэффициент вариации первого признака 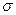(V =17,093%) меньше коэффициента вариации второго (V 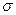= 22%), следовательно, средняя арифметическая величина признака «среднегодовая стоимость ОПФ» является более надежной характеристикой данной совокупности, чем средняя арифметическая признака «выпуск продукции».

г) симметричности распределений в центральной части ряда.

As = -0,21 (|As| ≤ 0,25), следовательно, асимметрия незначительная; распределение близко к нормальному.

Коэффициент асимметрии распределения признака «среднегодовая стоимость ОПФ» равен -0,21, следовательно, асимметрия незначительная (|As| ≤ 0,25); левосторонняя ( 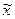< Mо), в распределении чаще встречаются значения признака большие, чем среднее значение.

Коэффициент асимметрии распределения признака «выпуск продукции» равен 0,015, следовательно, асимметрия незначительная (|As| ≤ 0,25); правосторонняя ( 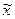> Mо), в распределении чаще встречаются значения признака меньшие, чем среднее.

Задача 5

В таблице 1.6 представлен расчет верхних и нижних границ интервала. Карман-это граница интервала. Частота показывает: сколько раз встречается данный вариант в вариационном ряду. Из интервального ряда распределения предприятий по стоимости основных фондов (Таблица 1.7) мы видим, что у четырех предприятий среднегодовая стоимость ОПФ находится в пределах от 1025 млн. руб. до 1255 млн. руб. и т.д. Гистограмма распределения едениц совокупности по признаку «среднегодовая стоимость основных фондов» представлена на рисунке 2. Форма теоретической кривой эмпирического распределения позволяет предположить, что закон распределения признака «среднегодовая стоимость основных фондов» - близкий к нормальному (Рис. 4).

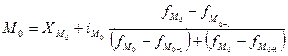
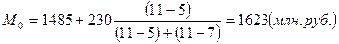
Для интервального ряда значение моды равно 1623 млн. руб., значение моды в вариационном ряду составляет 1657,5 млн. руб. Данные расхождения могут быть обусловлены тем, что при расчете моды для интервального ряда мы исходили из предположения о том, что распределение признака нормально, что на практике может давать некоторую погрешность в вычислениях.

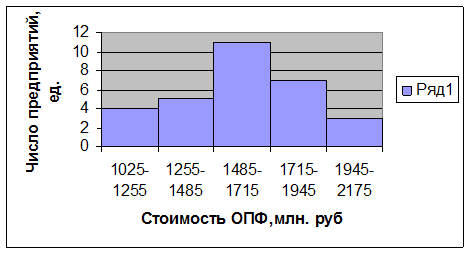
Рис. 4. Гистограмма и теоретическая кривая эмпирического распределения

СТАТИСТИЧЕСКИЙ АНАЛИЗ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ

Задача 1

Таблица 10 – Описательные статистики генеральной совокупности

По столбцу «Среднегодовая стоимость основных производственных фондов, млн.руб.»	По столбцу «Выпуск продукции, млн.руб»
Столбец1		Столбец2
Стандартное отклонение	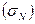278,1560899	Стандартное отклонение	331,8163307
Дисперсия выборки	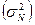77370,81034	Дисперсия выборки	110102,0773
Эксцесс	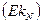-0,344943844	Эксцесс	-0,205332365
Асимметричность	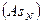-0,152503649	Асимметричность	0,042954448
Размах вариации (RN)	1668.936	Размах вариации (RN)	1990.896

Дисперсия генеральной совокупности 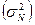может быть оценена по выборочной дисперсии : ;

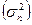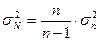По признаку «среднегодовая стоимость ОПФ»: .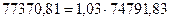

По признаку «выпуск продукции»: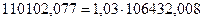

Таким образом, генеральные дисперсии признаков больше выборочных – в 1,03 раза или на 3%.

Для прогнозной оценки размаха вариации в генеральной совокупности используется соотношение: R = 6σ;

По признаку «среднегодовая стоимость ОПФ»:RN = 6·278,156 = 1668,936.

По признаку «выпуск продукции»:RN = 6·331,816 = 1990,896

Предельное значение амплитуды колебаний признака «среднегодовая стоимость ОПФ» в генеральной совокупности (RN) – 1668,936 млн. руб., что больше размаха вариации (Rn) в выборке в 1,45 раза или на 45%; RN признака «выпуск продукции» – 1990,896 млн. руб., что больше Rn в 1,44 раза или на 44%.

Задача 2

Таблица 11 – Предельные ошибки выборки и ожидаемые границы для генеральных средних

Доверии-тельная вероят- ность р	Коэффи-циент доверия, t	Предельные ошибки выборки	Ожидаемые границы для средних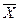
Для первого признака	Для второго	Для первого признака	Для второго
0,683	1,018	51,709	61,684	1548,291≤X≤1651,709	1438,296≤X≤1561,664
0,954	2,085	105,875	126,300	1494,125≤X≤1705,875	1373,68≤X≤1626,28
0,997	3,24	164,510	196,247	1435,49≤X≤1764,51	1303,733≤X≤1696,227

а) Средняя ошибка выборки:

по признаку «среднегодовая стоимость ОПФ»: ;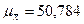

по признаку «выпуск продукции»: .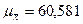

б) С вероятностью 0,683 можно гарантировать, что средняя годовая стоимость ОПФ предприятий генеральной совокупности находится в пределах от 1548,291 млн. руб. до 1651,709 млн. руб.

С вероятностью 0,954 можно гарантировать, что средняя годовая стоимость ОПФ предприятий генеральной совокупности находится в пределах от 1494,125 млн. руб. до 1705,875 млн. руб.

С вероятностью 0,997 можно гарантировать, что средняя годовая стоимость ОПФ предприятий генеральной совокупности находится в пределах от 1435,49 млн. руб. до 1764,51 млн. руб.

С вероятностью 0,683 можно гарантировать, что средняя величина выпуска продукции предприятий генеральной совокупности находится в пределах от 1438,296 млн. руб. до 1561,664 млн. руб.

С вероятностью 0,954 можно гарантировать, что средняя величина выпуска продукции предприятий генеральной совокупности находится в пределах от 1373,68 млн. руб. до 1626,28 млн. руб.

С вероятностью 0,997 можно гарантировать, что средняя величина выпуска продукции предприятий генеральной совокупности находится в пределах от 1303,733 млн. руб. до 1696,227 млн. руб.

Задача 3

Распределение единиц наблюдения по признаку «среднегодовая стоимость ОПФ» близко к нормальному, так как:

распределение единиц выборочной совокупности близко к нормальному;

выборка является репрезентативной (значение показателей генеральной и выборочной дисперсии расходятся незначительно);

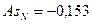, (|As| ≤ 0,25), следовательно, асимметрия незначительная;

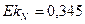, |Ek| незначительно отличается от нуля.

Распределение единиц наблюдения по признаку «выпуск продукции» близко к нормальному, так как:

распределение единиц выборочной совокупности близко к нормальному;

выборка является репрезентативной (значение показателей генеральной и выборочной дисперсии расходятся незначительно);

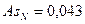, (|As| ≤ 0,25), следовательно, асимметрия незначительная;

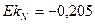, |Ek| незначительно отличается от нуля.