Способ пропорционального деления и долевого участия

Используется для моделей аддитивного и смешанного типа.

В первом случае: Y_а=а+в+с расчёт проводится так:

∆Y_а=∆Y_общ /(∆а+∆в+∆с )* ∆а

∆Y_в=∆Y_общ /(∆а+∆в+∆с )* ∆в

∆Y_с=∆Y_общ /(∆а+∆в+∆с )* ∆с

В моделях кратно-аддитивного вида сначала необходимо способом цепной подстановки определить, насколько изменился результатив­ный показатель за счет числителя и знаменателя, а затем произвести расчет влияния факторов второго порядка способом пропорциональ­ного деления

Например, уровень рентабельности повысился на 8% в связи с увеличением суммы прибыли на 1000 тыс.рубл.. При этом прибыль воз­росла за счет увеличения объема продаж на 500 тыс.рубл.., за счет рос­та цен - на 1700 тыс. рубл.., а за счет роста себестоимости продукции снизилась на 1200 тыс. рубл.. Исходные и рассчитанные данные отобразим в таблице 2.

Таблица 2.

Расчёт влияния факторов на результативный показатель способом долевого участия

Фактор	Изменение прибыли, тыс. руб.	Доля фактора в изменении общей суммы прибыли	Изменение уровня рентабельности, %
Объем продаж	+500
Цена	+1700
Себестоимость	-1200
Итого	+1000

Определим, как изменился уровень рен­табельности за счет каждого фактора:

∆R_Vрп=__________________________________

∆R_ц=__________________________________

∆R_{с =}__________________________________

Индексный метод

С помощью экономических индексов решаются следующие задачи:

• измерение динамики социально-экономического явления за два и более периодов времени;

• измерение динамики среднего экономического показателя;

• измерение соотношения показателей по разным регионам и т.п.;

Рассмотрим данный метод на примере, используя следующие формулы:

Формула агрегатного индекса товарооборота в фактических ценах: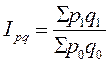

Формула агрегатного индекса физического объема всех товаров: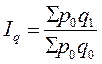

Формула агрегатного индекса цен (индекс цен Пааше):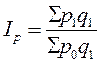

Разность между числителем и знаменателем индекса цен Пааше – абсолютный прирост выручки

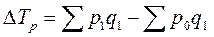
Исходные данные указаны в таблице 4.

Выяснить как изменились цены, товарооборот и количество всех проданных товаров в отчетном периоде по сравнению с базисным. А также рассчитать абсолютный прирост прибыли продавцов за счет повышения цен на товары.

Таблица 4.

Исходные данные для проведения анализа.

товар	Цена за 1 кг, грн	Выручка, тыс.грн	Кол-во прод.товаров, шт
баз. пер.	отч. пер.	баз. пер.	отч. пер.	баз. пер.	отч. пер.
А						8,4
Б						4,2

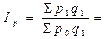
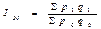
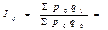
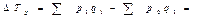
Ответ: цены в отчетном периоде по сравнению с базисным составили 112,2%, следовательно выросли на 12,2% ; выручка от реализации составила 126,2%, т.е. увеличился на 26,6% ; количество проданных товаров составило 112,5%, значит увеличилось на 12,5%. Абсолютный прирост выручки составил 25,2 тыс.рубл.

Корреляционный анализ

Используются для измерения влияния факторов в стохастическом анализе, когда взаимосвязь между показателями неполная, вероятностная.

Для двух случайных величин Х и Y корреляционный анализ состоит из следующих этапов:

- построение корреляционного поля и составление корреляционной таблицы;

- вычисление выборочного коэффициента корреляции;

- проверка статической гипотезы о значимости корреляционной связи.

В качестве примера для иллюстрации корреляционного анализа прямолинейной зависимости используем приведенные в табл. 3 данные об изменении уровня выработки рабочих (Y) в зависимости от уровня фондовооруженности труда (х).

Расчет уравнения связи (Y_x = а + bх) сводится к определению па­раметров а и b. Их находят из следующей системы уравнений:

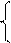na+b Σx= Σy

aΣx+b Σx^2=Σxy

n-число наблюдений (в данном примере 10);

x-фондовооруженность труда (стоимость x-основных произ­водственных фондов на одного работника предприятия), тыс. рубл..;

y-среднегодовая выработка продукции одним работником, тыс. рубл..

Таблица 4

Расчет производных данных для корреляционного анализа

n	X	У	ху	X2	У2	Yx
	3,1	4,5
	3,4	4,4
	3,6	4,8
	3,8	5,0
	3,9	5,5
	4,1	5,4
	4,2	5,8
	4,4	6,0
	4,6	6,1
	4,9	6,5
Итого

Подставим полученные значения в систему уравнений:

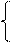; + 162,76b = 219,45.

Умножив все члены первого уравнения на 4, получим:

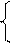40а + 160 b = 216;

40а + 162,76b = 219,45.

Вычтя из второго уравнения первое, узнаем, что 2,76 b = 3,45. Отсюда b = 3,45/2,76 = 1,25.

а=(54+(40/1,25))/10=0,4

Уравнение, описывающее зависимость производительности труда от его фондовооружённости, получило следующее выражение:

Y_x = 0,4+l,25x.

Коэффициент а — постоянная величина результативного показа­теля, которая не связана с изменением данного фактора. Пара­метр b показывает среднее изменение результативного показателя с повышением или понижением величины факторного показателя на единицу его измерения. В данном примере с увеличением фондово­оруженности труда на 1 тыс. рубл.. выработка рабочих повышается в среднем на 1,25 тыс. рубл..

Y_x = 0,4+1,25-3,1 =4,28.