Методы измерения связей между количественными признаками

Методы изучения функциональных связей:

1) балансовый метод;

2) индексный метод (см. тема 9).

В статистике широко используют балансовые построения, как метод анализа связей и пропорций в экономике. Статистический баланс представляет собой систему показателей, которая состоит из двух сумм абсолютных величин, связанных между собой знаком равенства:

А+С=D+E

Посредством балансов связывают в единую систему абсолютные величины, характеризующие движение ресурсов. Простейшим балансом такого рода является баланс оборотных средств какой-либо организации. Суммы показателей в нём образуют начальный и конечный остатки, поступление и расход. Эта система может быть изображена таким балансовым равенством:

остаток начальный + поступление – расход = остаток конечный

Приведённая балансовая формула характеризует процесс движения оборотных средств и показывает взаимосвязь и пропорции отдельных элементов этого процесса. Поступление и расход должны быть в определённом соответствии. Если это соответствие нарушается, то резко меняется удельный вес запасов к концу периода по сравнению с начальным. Поэтому нормальный ход процесса требует определённой пропорциональности между всеми элементами баланса.

Методы изучения корреляционных взаимосвязей

ü Между атрибутивными признаками – метод взаимной сопряжённости.

ü Между количественно – варьирующими:

1) метод параллельных рядов;

2) графический метод (корреляционного поля);

3) табличный метод (корреляционной таблицы);

4) метод аналитических группировок;

5) корреляционно – регрессионный анализ

Регрессионный анализ

Корреляционно-регрессионный анализ предполагает установление аналитической формы связи (регрессионный анализ) и измерение тесноты, направления связи (корреляционный анализ).

Наиболее часто для характеристики регрессии используют следующие типы функций:

Линейная регрессия

У_х = а₀ + а₁Х или У_{1, 2,3 …п} = а₀ + а₁Х₁ + а₂Х₂ + … + а_пХ_п

Параболическая связь

У_х = а₀ + а₁Х + а₂Х² или У_{1, 2, 3…п} = а₀ + а₁Х₁² + а₂Х₂² + … + а_пХ_п²

Гиперболическая связь

У_х = а₀ + а₁ 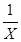или У_{1, 2, 3…п} = а₀ +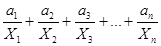

Полулогарифмическая кривая

У_х = а₀ + а₁lg Х

Логистическая кривая

У_х =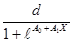

Показательная функция

У_х = а₀а₁^Х или У_{1, 2, 3…п} = е^{А0 + А1Х1 +А2Х2 + … АпХп}

Степенная функция

У_х = а₀Х^а1 или У_{1, 2, 3,…п} = а₀Х₁^А1· Х₂^А2 · Х₃^А3….Х_п^Ап

Оценка параметров уравнений регрессии (а₀, а₁, а₂…а_п) осуществляется методом наименьших квадратов. Сущность его заключается в минимизации суммы квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии.

Каждый коэффициент регрессии показывает, на сколько в среднем изменится величина результативного признака в случае изменения факторного признака на единицу при фиксированном положении остальных факторов.

Значимость коэффициентов регрессии осуществляется с помощью t- критерия Стьюдента:

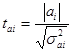
входные параметры: α, ν = п – к - 1,

Если t_факт > t_табл, то параметр модели принимается значимым

где

σ²_аi – дисперсия коэффициентов регрессии;

α – уровень значимости критерия о равенстве нулю параметров;

ν – число степеней свободы;

п - количество единиц совокупности;

к – число факторных признаков в уравнении;

Адекватность корреляционно-регрессионной модели осуществляется с помощью F- критерия Фишера:

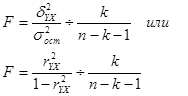
входные параметры: α, ν₁ = к, ν₂ = п-к-1,

где

r²_УХ – коэффициенты детерминации.

Если F_факт > F_табл, то можно утверждать о надежности построенного уравнения.

Для характеристики корреляции применяют показатели тесноты связи между явлениями. Они различаются в зависимости от формы и вида связи.

Корреляционный анализ

Линейный коэффициент корреляции

- используется для изучения связи между двумя признаками в случае наличия между ними линейной зависимости и определяется по формуле:

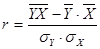
Линейный коэффициент корреляции изменяется в пределах от –1 до 1 и выражает характер связи, чем ближе значение коэффициента к 1 (-1), тем теснее связь между признаками.

если 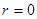, то связь отсутствует;

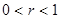, связь прямая и однонаправленная;

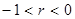, связь обратная;

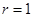(-1), связь функциональная.

В том случае когда исходная информация представлена в виде корреляционной таблицы необходимо учесть частоты повторений как индивидуальных значений факторного и результативного признаков, так и число повторений данного сочетания их значений. В этом случае формула коэффициента корреляции будет иметь вид:

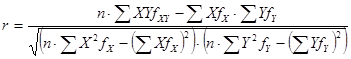
Эмпирическое корреляционное отношение

- рассчитывается по данным группировки в случае не линейной зависимости между признаками и определяется по формуле:

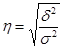, где

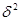- межгрупповая дисперсия, характеризующая вариацию результативного признака, обусловленную группировочным признаком;

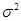- общая дисперсия результативного признака.

Изменяется этот показатель в пределах от 0 до 1. Интерпретация значений коэффициента такова:

-если 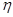находится в пределах 0,1-0,3, то связь слабая;

- 0,3-0,5 – связь умеренная;

- 0,5-0,7 – связь заметная;

- 0,7-0,9 – связь высокая;

- 0,9-0,99 – связь очень высокая.

Индекс корреляции (теоретическое корреляционное отношение)

- используется для измерения связи при любой её форме и определяется по формуле:

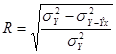, где

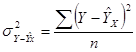- дисперсия отклонений;

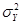- дисперсия фактических значений результативного признака;

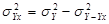- дисперсия теоретических значений результативного признака.

Индекс корреляции изменяется в пределах от 0 до 1. Если он равен нулю, то связи между признаками У и Х нет. Чем он ближе к 1, тем связь между признаками теснее.

Частные коэффициенты корреляции

- применяется для характеристики тесноты связи между двумя признаками при фиксированном значении других признаков и определяется по формуле:

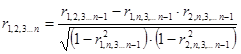
Коэффициент множественной корреляции

- в случае оценки связи между результативным (У) и двумя факторными (Х₁, Х₂) признаками множественный коэффициент корреляции имеет вид:

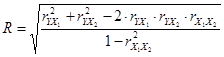, где

r – парные коэффициенты корреляции между признаками.

Его значения находятся в пределах от 0 до 1. Чем ближе значение коэффициента к единице, тем теснее связь между признаками.

Множественный коэффициент корреляции можно рассчитать, используя парные коэффициенты корреляции (r_УЧ) и β – коэффициенты:

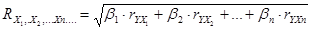
Коэффициент детерминации

- показывает какая доля вариации изучаемого результативного признака объясняется влиянием факторов, включенных в уравнение множественной регрессии и представляет собой квадрат коэффициента корреляции:

d = r² ·100% или d = R² ·100%.

Изменяется в пределах от 0 до 100 и характеризует, на сколько процентов изменение результативного признака зависит от выбранных в модель факторных признаков. Остальные проценты (до 100) показывают влияние других, не учтенных в модели признаков.

Значимость линейного коэффициента корреляции проверяется на основе t- критерия Стьюдента:

- если объём совокупности (n) < 50 единиц, то формула критерия имеет вид

,

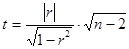входные параметры:

.

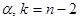Если расчетное значение t>t_Т, то коэффициент корреляции принято считать значимым.

Если объём совокупности (n) более 100 единиц, то используется формула:

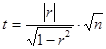
Проверка значимости коэффициента множественной корреляции осуществляется на основе F–критерия Фишера:

,

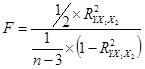входные параметры:

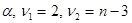
Если F>F_Т, то коэффициент множественной корреляции считается значимым.

Для выявления влияния каждого отдельного фактора на результативный признак вычисляют стандартизированные коэффициенты (коэффициенты эластичности и β - коэффициенты):

Коэффициенты эластичности (α- коэффициент)

Э 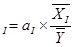, где

а_i – коэффициент регрессии при i–м факторе;

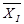- среднее значение i–го фактора;

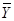- среднее значение результативного признака.

Коэффициент эластичности показывает, на сколько % в среднем изменится результативный признак с изменением на 1% каждого факторного признака при фиксированном значении других факторов.

β- коэффициенты

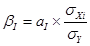, где

σ_Х – среднее квадратическое отклонение i–го фактора;

σ_У – среднее квадратическое отклонение результативного признака.

Бета коэффициент показывает, на какую часть среднего квадратического отклонения изменится результативный признак при изменении соответствующего факторного признака на свое среднее квадратическое отклонение.

Контрольные вопросы для самоподготовки:

1. Понятие о связях между явлениями. Виды и формы корреляционной зависимости. Методы исследования связей (графический, группировок, параллельных рядов).

2. Однофакторный и многофакторный корреляционно -регрессионный анализ. Проверка построенной модели на адекватность и мультиколлинеарность. Показатели тесноты связи: линейный коэффициент корреляции, индекс корреляции, эмпирическое и теоретическое корреляционное отношение. Коэффициент детерминации.

3. Непараметрические методы оценки связей. Коэффициенты ассоциации, контингенции, корреляции рангов Спирмена, Кенделла, коэф-т корреляции знаков Фехнера.

4. Применение КРМ в анализе и прогнозе. Автокорреляция и авторегрессия.

Список использованной литературы

Нормативно-правовые акты

1. Федеральный закон «Об официальном статистическом учете и системе государственной статистики в Российской Федерации» от 29 ноября 2007 года № 282-ФЗ.

2. Приказ Ростехрегулирования №329-ст от 22 ноября 2007 г. «О внедрении Общероссийского классификатора продукции по видам экономической деятельности (ОКПД)»

3. Федеральная целевая программа Развитие государственной статистики России в 2007-2011 годах.

4. Методологические положения по статистике. — М.: Росстат 2006 — Вып.5.

Базовый учебник

1. Статистика: Учебно-практич. пособие / Под. ред. М.Г. Назарова.- М.:КНОРУС,2006*;

2. Социально-экономическая статистика. Практикум / под ред. С.А. Орехова. – М.: Эксмо, 2007. – 384 с.*

Основная литература

1. Теория статистики: Учебник / Под ред. Р.А. Шмойловой.-5-е изд.- М.: Финансы и статистика, 2005;*

2. Практикум по теории статистики. Учебное пособие. /Под ред. Шмойловой Р.А. - М.: Финансы и статистика, 2002*;

3. Статистика финансов: Учеб. Пособие / под ред.М.Г. Назарова. – М: Омега-Л, 2005. – 380 с.*

4. Статистика: Учебник / Под ред. В.Г. Ионина.-3-е изд., перераб. и доп.-М.: ИНФРА-М, 2006*

Дополнительная литература

1. Статистика: Учебник / Под ред. И.И. Елисеевой.-М.: Высшее образование, 2006*;

2. Гусаров В.М. Статистика: Учеб. пособие для вузов. - М: ЮНИТИ-ДАНА, 2001*;

3. Статистика: Учебник / Под ред. B.C. Мхитаряна.-М.: Экономистъ, 2005*;

4. Статистика: Учеб.пособие / Под ред. В.М. Симчеры.- М.: Финансы и статистика, 2005*;

5. Салин В.Н., Чурилова Э.Ю. Курс теории статистики для подготовки специалистов финансово-экономического профиля: Учебник. - М.: Финансы и статистика, 2006*;

6. Журнал «Вопросы статистики».