Вопрос 1. Понятие банка и банковских операций

Министерство науки и образования Российской Федерации

Уральский государственный лесотехнический университет

Кафедра бухгалтерского учета и аудита

Д.Ю. Захаров

Методические указания

Для самостоятельной работы

по дисциплине «Финансы и кредит»

Для студентов специальности 080502.65, 080507.65

Екатеринбург

ВВЕДЕНИЕ

В соответствии с учебным планом студенты ФЭУ специальностей 080502.65, 080507.65 выполняют самостоятельную работу по дисциплине «Финансы и кредит».

В качестве методического обеспечения самостоятельной работы студент может использовать данный теоретический материал, а также знакомиться с указанными литературными и электронным источниками.

Для ознакомления с практикой финансовых расчетов в МУ приводятся наиболее часто используемые формулы финансовой математики. В каждой задаче исходные данные представлены в 10 вариантах. Студент выбирает номер своего варианта по последней цифре номера зачетной книжки. Студент делает расчеты по приведенным задачам и отвечает на теоретические вопросы в соответствии с программой курса.

Студенты, выполнив самостоятельную работу, оформляют ее в соответствии с общими тре­бованиями УГЛТУ, предоставляют для проверки на кафедру бухгалтерского учета и аудита и после доработки защищают.

Задачи

Под процентами в финансовых расчетах понимают сумму дохо­дов от предоставления денег в долг в любой форме: единовремен­ная ссуда, помещение денег на депозит, покупка облигации, учет векселя и т.д. Интервал, за который начисляют проценты, называют периодом начисления.

Проценты выплачиваются кредитору или по мере их начисле­ния, или присоединяются к сумме долга. При начислении и удержа­нии процентов после выдачи кредита применяют процентные ставки. При начисле­нии и удержании процентов из суммы кредита в начале срока опера­ции применяют учетные ставки. Ставки процентов могут применяться к одной и той же начальной сумме на протяжении всего срока ссуды (простые ставки) или к сумме с начисленными в преды­дущем периоде процентами (сложные ставки).

Ставки могут быть фиксированными или плавающими. Фиксированные ставки являются неизменными на протяжении всего срока ссуды, плавающие ставки изменяются в большую или меньшую сторону при истечении определенного срока.

Рассмотрим начисление процентов по простым процентным ставкам. Сумма долга при фиксированной процентной ставке опре­деляется по формуле:

С = К (1 + n · СП), (1.1)

где С – сумма долга на конец срока ссуды, руб.;

К – первоначальная сумма кредита, руб.;

СП – годовая процентная ставка в долях;

n – продолжительность кредита в годах.

n = 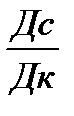, (1.2)

где Д_с – число дней ссуды;

Д_к – временная база для расчета процентов (продолжитель­ность года), дней.

Д_с определяется или точно (берется фактическое число дней ссуды), или приближенно (продолжительность любого полного ме­сяца принимается 30 дней, неполного по факту). Проценты начисляются или в половинном размере за день выдачи и день погашения ссуды, или в полном размере в день погашения (день выдачи ссуды не учитывается). Д_к при точных расчетах берется 365 или 366, а при приближенных 360 дней. Исходя из сказанного приме­няют три метода начисления простых процентов:

а) точные проценты (дает самые точные результаты);

б) обыкновенные проценты с точным числом дней ссуды и Д_к = 360 дней;

в) обыкновенные проценты с приближенным числом дней ссуды и Д_к = 360 дней;

Сумма долга при плаваю­щей процентной ставке определяется по формуле:

С = К (1 + 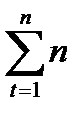_t · СП_t ), (1.3)

где n_t – продолжительность периода начисления процентов в периоде t в годах;

СП_t - ставка процентов в периоде t в долях.

Сумма долга при начислении по простой учетной ставке рас­считывается так:

С = 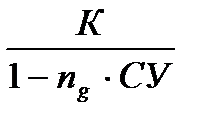при n > n_g · CУ (1.4)

где СУ – годовая учетная ставка в долях;

n_g – продолжительность до погашения ссуды в годах.

n_g = 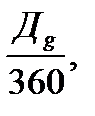(1.5)

где 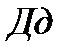- число дней до погашения ссуды (всегда берется точно).

В финансовой практике часто сталкиваются с задачей, обрат­ной определению суммы долга: по заданной сумме С, которую сле­дует уплатить через время n, необходимо рассчитать сумму полу­ченной ссуды К. В этом случае говорят, что сумма С дисконтиру­ется, а разность между С и К называют дисконтом. Исходя из целей дисконтирования и вида процентной ставки применяют два способа расчета: математическое дисконтирование и банковский учет.

Математическое дисконтирование имеет место при применении простой процентной ставки:

К = 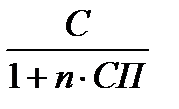(1.6)

Банковский учет предполагает использование простой учетной ставки:

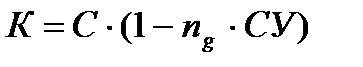(1.7)

Данный вид учета применяют при покупке (учете) векселей и других краткосрочных обязательств. Суть операции заключается в том, что банк до наступления срока платежа по векселю покупает его у владельца по цене, меньше той суммы, которая должна быть выплачена по нему в конце срока, т.е. приобретает его с дисконтом. Получив при наступлении срока векселя деньги, банк реализует дисконт. Однако следует помнить, что применение учетной ставки для дисконтирования при относительно большом сроке уплаты по векселю и значительной учетной ставке может привести к нулевой или даже отрицательной сумме К, т.е. обязательно должно выпол­няться условие 1 > n_g · СУ.

Операции начисления простых процентов и дисконтирования по учетной ставке могут совмещаться, например, при учете платежного обязательства, предусматривающего начисление простых процен­тов.

Учет платежного обязательства в таком случае можно предста­вить так:

С_У = К (1 + n₁ · СП) (1 – n₂ · СУ), при n₁ ≥ n₂ (1.8)

где С_У – сумма, получаемая при учете обязательства, руб;

n₁ – срок начисления процентов (общий срок платежного обязательства) в годах;

n₂ – срок от момента учета обязательства до даты погаше­ния долга, в годах.

При изменении условий кредитного договора, при объедине­нии платежей или замене одного платежа несколькими с разными сроками, при изменении срока платежа участвующие в сделке сто­роны обычно руководствуются принципом финансовой эквивалент­ности платежей. Этот принцип предполагает: во-первых, постоянство финансо­вых обязательств сторон до и после изменений условий договора; во-вторых, эквивалентными считаются платежи, которые будучи приведенными к заданному моменту времени, оказываются равными. Рассмотрим консолидацию платежей.

Пусть объединяются платежи С₁, С₂, … С_i со сроками n₁, n₂,…n_к. Сумма платежа по новому условию С_о, его срок n_о. Консолидация платежей осуществляется следующим образом:

n_о > n₁, n₂,…n_i или n_о > n_i

по процентной ставке:

С_о = 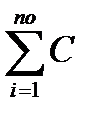_i (1 + Т_i · СП); (1.9)

по учетной ставке:

С_о = 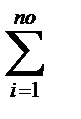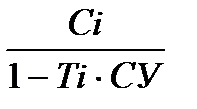; (1.10)

где Тi – временной интервал между сроками n₀ и n_i 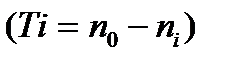в годах;

n₀ < n₁, n₂, …, n_k или n₀ < n_k

по процентной ставке:

С_о = 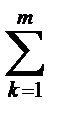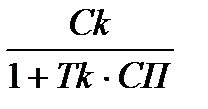; (1.11)

по учетной ставке:

С_о = 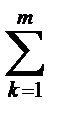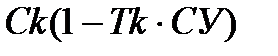; (1.12)

n_i < n_о < n_к

по процентной ставке:

С_о = 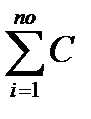_i (1 + Т_i · СП) + 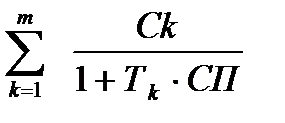(1.13)

где С_i - сумма объединяемых платежей со сроками n_i ;

С_к – сумма объединяемых платежей со сроками n_к (Т_к = n_{к ­}– n_о).

по учетной ставке:

С_о = 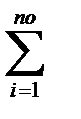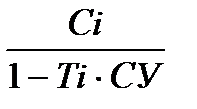+ 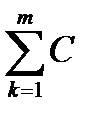_к (1 - Т_к · СУ) (1.14)

Продолжительность срока ссуды при консолидации платежей с разными сроками может быть определена для двух вариантов:

величина нового платежа равна сумме заменяемых плате­жей С₀= 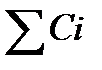, тогда срок нового платежа

n₀ = 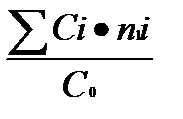; (1.15)

величина нового платежа задается, при этом С₀ ≠ 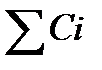, то­гда срок нового платежа

n₀ = 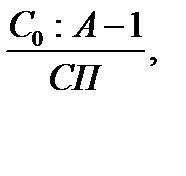С₀ > А (1.16)

где А – сумма ссуд, приведенных на дату их выдачи (сумма первоначально выданных кредитов).

Сумма долга при применении фиксированных сложных процентов рассчитывается при начислении 1 раз в год по формулам:

по процентной ставке:

С = К • (1 + СП)ⁿ (1.17)

по учетной ставке:

С = 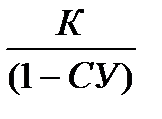_n СУ < 1 (1.18)

Начисление сложных процентов часто осуществляется не один, а несколько (пусть р) раз в году. В этом случае сумма долга со­ставит:

С = К (1 + СП : р)^N, (1.19)

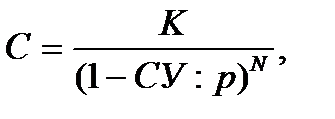(1.20)

где N – число периодов начисления (N = n · р).

При применении плавающих сложных процентов сумма долга будет рассчитываться так:

начисление по сложным процентным ставкам:

1 раз в год С = К (1 + СП₁) (1 + СП₂) • … (1 + СП_t) (1.21)

р раз в год С = К (1 + СП₁ : р)^р (1 + СП₂ : р)^р • … (1 + СП_t : р)^р , (1.22)

где СП₁, СП₂, …, СП_t – ставка процентов соответственно в 1-ый, 2-ой и

t-ый год в долях.

Аналогично рассчитывается сумма долга и при применении плавающих сложных учетных ставок.

Во всех рассмотренных выше формулах все денежные вели­чины измерялись по номиналу, т.е. инфляция во внимание не при­нималась. Для компенсации инфляции необходимо корректировать процентные ставки по следующей формуле:

СП_и = СП + СП · И + И, (1.23)

где СП – годовая ставка процентов, характеризующая реальную доходность ссудной операции, в долях;

И – годовой темп инфляции, в долях;

СП_и – ставка процентов, учитывающая инфляцию, в долях.

Дисконтирование по сложным ставкам производится аналогично дисконтированию по простым ставкам (формулы 1.6, 1.7)

Определение продолжительности ссуды по простым и сложным процентным ставкам производится по следующим формулам:

сложная ставка:

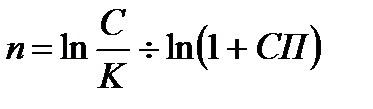(1.24)

простая ставка:

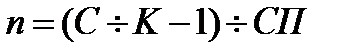(1.25)

Задача 1

Определить размер погасительного платежа при начислении процентов по простым, сложным процентным и учетным ставкам (начисление сложных ставок 1 раз в год и ежемесячно). Кредит выдан на 3 года. Размер ссуды и ставку процентов взять из табл. 3.

Таблица 1

Номер варианта	Размер ссуды, тыс. руб	Процент годовых, %	Номер варианта	Размер ссуды, тыс. руб.	Процент годовых, %

Прим. Воспользоваться формулами: 1.1, 1.4, 1.17, 1.18, 1.19 и 1.20

Задача 2

Определить размер погасительного платежа, используя три метода расчета ссуды по простым фиксированным процентным ставкам. Исходные данные по вариантам приведены в табл. 2.

Таблица 2

Номер варианта	Размер ссуды, тыс. руб.	Дата выдачи ссуды	Дата погашения ссуды	Процент годовых, %
		6 января	10 ноября
		18 января	1 ноября
		15 февраля	5 декабря
		4 января	4 ноября
		10 февраля	19 декабря
		15 января	15 ноября
		24 января	20 ноября
		23 марта	23 декабря
		12 января	2 ноября
		1 марта	15 декабря

Прим.: воспользоваться формулами 1.1 и 1.2

Задача 3

Наращенная сумма составляет 650 тыс.руб. Продолжительность ссуды принять из задачи 2. Первоначальная ставка процентов – 20% годовых, каждые два месяца она увеличивается на 3% годовых. Определить размер выданной ссуды.

Прим.: воспользоваться формулой 1.3

Задача 4

Должник выдает кредитору вексель, по которому через определенный срок будет уплачено 80 тыс. руб., включая проценты. Кредитор продает вексель банку до наступления срока платежа. Определить сумму первоначального долга и сумму, полученную кредитором от банка.

Прим.: воспользоваться формулами 1.6 и 1.7

Исходные данные по вариантам приведены в табл. 3.

Таблица 3

Номер варианта	Дата выдачи векселя	Дата оплаты векселя	Дата продажи векселя банку	Годовая процентная ставка, %	Годовая учетная ставка, %
	15 апреля	29 июля	1 июля
	14 января	4 мая	5 апреля
	20 марта	20 августа	20 июля
	18 февраля	8 апреля	18 марта
	10 мая	25 августа	12 июля
	15 августа	5 декабря	4 октября
	12 июня	2 августа	10 июля
	15 июля	10 октября	12 сентября
	14 сентября	14 ноября	5 ноября
	10 марта	11 августа	30 июля

Задача 5

Четыре платежа со сроком 25 апреля, 10 июня, 25 июля и 4 августа (их суммы приведены по вариантам в табл. 4) решено объединить: срок – 5 июля с процентной ставкой 15% годовых. Определить сумму консолидированного платежа.

Таблица 4

Номер варианта	Сумма платежа, тыс. руб.
1-го	2-го	3-го	4-го

Прим.: воспользоваться формулами: 1.23, 1.6 и 1.13

Задача 6-10 находится в файле с образцом решения

Часть 2.Теретическая часть.

Вопрос 1. Понятие банка и банковских операций.

Банк (от итал. banco — лавка, стол, на которых менялы раскладывали монеты) — кредитно-финансовое учреждение. Основной функцией банков является аккумуляция денег населения и фирм в виде депозитов и других счетов, в целях их размещения на возмездной основе в проекты (в виде прямого или косвенного финансирования проектов) и другие финансовые инструменты (ценные бумаги, депозиты Центрального банка и др.).

В соответствии с Федеральным законом «О банках и банковской деятельности» № 395-1 от 2 декабря 1990г., банк — кредитная организация, которая имеет исключительное право осуществлять в совокупности следующие банковские операции: привлечение во вклады денежных средств физических и юридических лиц, размещение указанных средств от своего имени и за свой счёт на условиях возвратности, платности, срочности, открытие и ведение банковских счетов физических и юридических лиц.

На 01.01.2008 в Российской Федерации действовало 1 253 кредитных организаций, в т.ч. в УФО 62.

Банковские операции – операции банков по привлечению денежных средств и их размещению, выпуску в обращение и изъятию из него денег, осуществление расчетов и т.п. Различают пассивные банковские операции, активные банковские операции и комиссионные банковские операции.

Банковские операции — закрытый перечень операций, право совершения которых принадлежит банкам на исключительной основе. Все банковские операции и другие сделки осуществляются в рублях, а при наличии соответствующей лицензии Банка России — и в иностранной валюте. Правила осуществления банковских операций, в том числе правила их материально-технического обеспечения, устанавливаются Банком России.

К банковским операциям, например, относятся:

1. привлечение денежных средств физических и юридических лиц во вклады и депозиты (до востребования и на определённый срок);

2. размещение привлечённых средств от своего имени и за свой счёт.

Кредитная организация, кроме перечисленных операций, вправе осуществлять отдельные сделки, например:

1. выдачу поручительств за третьих лиц, предусматривающих исполнение обязательств в денежной форме;

2. приобретение права требования от третьих лиц исполнения обязательств в денежной форме.

Активные банковские операции - операции, посредством которых банки размещают имеющиеся в их распоряжении ресурсы с целью получения прибыли. Наиболее распространенными формами активных операций являются: предоставление денежных средств в кредит под проценты, вложения в ценные бумаги, инвестиции в производство.

Пассивные банковские операции - операции, посредством которых банки формируют свои ресурсы для проведения кредитных и других активных операций банка.

В ходе самостоятельного изучения материала по данному вопросу студенту необходимо:

1. Дать определения и понятия: банк, кредитная организация, небанковская кредитная организация, банковская система.

2. Указать все банковские операции и сделки в соответствии с законодательством^*.

3. Охарактеризовать активные и пассивные банковские операции.

^*См. Федеральный закон №395-1 «О банках и банковской деятельности» http://base.consultant.ru/cons/cgi/online.cgi?req=doc;base=LAW;n=75346