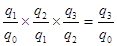Средние индексы. Индексы средних уровней качественных показателей

Если любой качественный индексируемый показатель (себестоимость, цену, производительность труда и т.д.) обозначить через x, а его веса – через f, то динамику среднего показателя (средней себестоимости, средней цены, средней производительности труда и т.д.) можно отразить как за счет изменения обоих факторов (x и f), так и за счет каждого фактора отдельно. Так, например, средняя производительность труда на предприятии может возрасти за счет ее повышения у рабочих отдельных специальностей и повышения удельного веса рабочих с более высокой производительностью труда в общей численности рабочих.

Совместное действие указанных факторов на общее изменение динамики среднего уровня явления, а также роль каждого фактора в отдельности в общей динамике средней выявляются в статистике при помощи системы взаимосвязанных индексов: индекса переменного состава, индекса постоянного состава и индекса структурных сдвигов.

Индекс переменного состава – это индекс, выражающий соотношение средних уровней изучаемого явления, относящихся к разным периодам времени. Индекс характеризует изменение среднего уровня признака за счет влияния двух факторов.

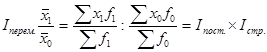
Индекс переменного состава разлагается на два индекса-сомножителя: индекс постоянного (фиксированного) состава и индекс структурных сдвигов.

Индекс постоянного состава

Характеризует изменения значений осредняемого признака (х) у отдельных единиц совокупности:

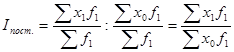
Индекс структурных сдвигов

Дает характеристику структурных изменений, под которыми понимается изменение доли отдельных единиц совокупности в общей их численности ( ).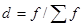

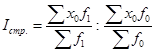
Если в индексах средних уровней в качестве весов используются удельные веса единиц совокупности в общей численности совокупности (показатели доли 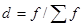), то система индексов может быть записана в следующем виде:

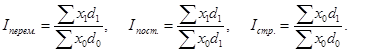
Абсолютный прирост (уменьшение) среднего уровня признака в целом по совокупности находится как разность числителя и знаменателя индекса переменного состава:

.

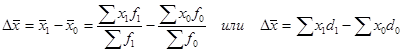Абсолютный прирост (уменьшение) среднего уровня признака в целом по совокупности за счет отдельных факторов рассчитывается как разность числителей и знаменателей индексов постоянного состава и структурных сдвигов:

- за счет изменения значений изучаемого признака у отдельных единиц совокупности:

,

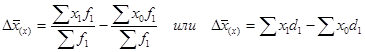- за счет структурных изменений:

.

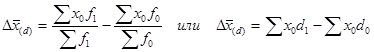В общем виде: .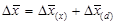

Цепные и базисные индексы

Индивидуальные индексы

Индекс физического объема

базисныецепные

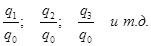
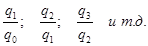
Индекс цен

базисные цепные

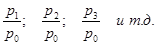
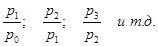
Цепные индексы получаются из базисных путем деления данного базисного индекса на предыдущий:

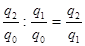
. Произведение последовательных цепных индексов дает базисный индекс последнего периода: