Годовая рента с начислением процентов по номинальной процентной ставке

В рассматриваемом случае проценты начисляются m раз в году по ставке j/m, где m- номинальная ставка.

Наращенная сумма ренты равна:

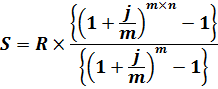
Задача 19. В фонд ежегодно в конце года поступают средства по 10 000 рублей в течение 3 лет, на которые начисляются проценты по номинальной ставке 15% годовых, причем проценты начисляются поквартально. Определите величину фонда на конец срока.

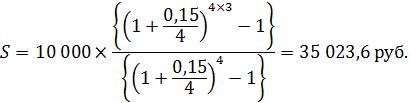
Рента с неоднократными выплатами в году

Выплаты производятся Р раз в году, поэтому рента называется р-срочной. Сумма всех ежегодных платежей в течение n лет, вычисляется по формуле:

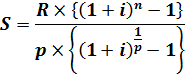
Задача 20.В фонд ежегодно поступают средства по 5000 рублей в течение 7 лет, на которые начисляются проценты по ставке 15% годовых, причем выплаты производятся поквартально. Определите величину фонда на конец срока.

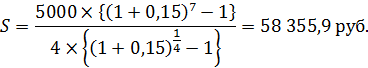
Рента с начислением процентов по номинальной процентной ставке и с неоднократными выплатами в году.

В любом году производится р выплат по R/р руб., где R – годовая рента. Количество начислений процентов в году по номинальной процентной ставке j равно m. Наращенная сумма на все выплаты к концу срока определяется формулой:

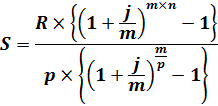
Формула для частного случая, когда количество начислений процентов в году равно количеству выплат в году:

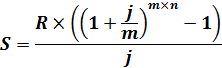
Задача 21.В фонд ежегодно поступают средства по 5000 рублей в течение 7 лет, на которые начисляются проценты по ставке 15% годовых, причем все выплаты производятся поквартально, а проценты начисляются ежемесячно. Определите величину фонда в конце срока.

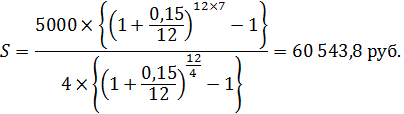
Задача 22. В фонд ежегодно поступают средствапо 10000 руб в течение 7 лет, на которые начисляются проценты по ставке 15% годовых, причем проценты начисляются и выплаты производятся ежемесячно. Определите величину фонда на конец срока.

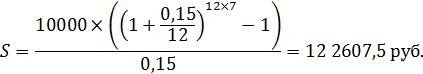
Задания для семестровой (контрольной) работы

Задача 1.

Какова должна быть продолжительность ссуды (в днях) для того, чтобы долг, равный Р тысяч рублей, вырос до S тысяч рублей, при условии, что простая ставка наращения равна i% годовых (при К=365)?

№ варианта

P

S

i

Задача 2.

В контракте предусматривается погашения обязательства в сумме S тысяч рублей через n дней. Первоначальная сумма долга составляет P тысяч рублей. Определите доходность ссудной операции в виде простой годовой ставки наращения (К=365)

№ варианта

P

S

n

Задача 3.

Какой величины достигнет долг, равный P тысяч рублей через n года при росте по сложной ставке наращения j % годовых при начислении процентов m раз в году?

№ варианта

P

n

m

j

Задача 4.

Банк выдал кредит на 6 месяцев в сумме P тыс. рублей. Ожидаемый месячный уровень инфляции 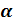%, требуемая реальная доходность операции равна i % годовых. Определите ставку процентов по кредиту с учетом инфляции, размер наращенной суммы и величину процентного платежа.

№ варианта

P

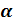i

Задача 5.

Кредит в сумме P млн. рублей выдан на n лет. Реальная эффективность должна составлять i % годовых (сложные проценты). Расчетный уровень инфляции составляет 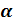% в год. Определите ставку процентов при выдаче кредита, также наращенную сумму.

№ варианта

P

n

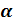i

Задача 6.

Кредит в сумме P млн. рублей выдан на n лет. На этот период прогнозируется рост цен в In раза. Определите ставку процентов при выдаче кредит и наращенную сумму долга, если реальная доходность должна составлять i % годовых по ставке сложных процентов.

№ варианта
P
n
In	1,5	1,7	2,1	1,8	1,3	1,6	1,9	1,7	1,6	2,2	1,8	1,4	1,7	2,1	2,3
i

Задача 7.

Фирма имеет ряд финансовых обязательств перед одним кредитором - 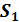млн. рублей, 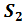млн. рублей и 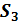млн. рублей, которые должна погасить соответственно через 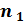, 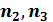дней после 01.01 текущего года. По согласованию сторон решено заменить их одним платежом, равным So млн. рублей, с продлением срока оплаты, используя процентную ставку i % годовых (простые проценты).Определите срок уплаты консолидированного платежа.

№ варианта
S1		2,4			2,4			2,4			2,4			2,4
S2		2,7	3,2		2,7	3,2		2,7	3,2		2,7	3,2		2,7	3,2
S3	2,5	3,2	2,8	2,5	3,2	2,8	2,5	3,2	2,8	2,5	3,2	2,8	2,5	3,2	2,8
n1
n2
n3
So		9,5	10,2	9,2	9,6	10,1	10,2	9,7	10,3	9,3	9,8	10,6	9,2	9,4	10,3
i

Задача 8.

Фирма получила кредит на сумму P тысяч рублей под i % годовых (простые проценты). Кредит должен быть погашен двумя платежами : первый- P₁ тысяч рублей с процентами через n₁ дней, второй – P₂ тысяч рублей с процентами через n₂ дней. Впоследствии фирма договорилась с кредитором об объединении платежей в один со сроком погашения n₀ дней. Необходимо определить размер консолидированного платежа (К=365).

№ варианта

P1

P2

P

n1

n2

n0

i

Список рекомендуемой литературы

Основная:

1. Ковалев В.В. Сборник задач по финансовому анализу. – М.: Финансы и статистика, 2007

2. Кочовович Е. Финансовая математика с решениями и задачами: учебно-метод. пособие. – М.: Финансы и статистика, 2005

3. Кузнецов Б.Т. Финансовая математика. – М.: Экзамен, 2005

4. Управление инвестициями /под ред. В.В. Шеремета. – М.: Высшая школа, 2003

5. Черкасов В.Е. Практическое руководство по финансово-экономическим расчетам. –М.: Метаинформ, 2005

6. Четыркин Е.М. Финансовая математика. - М.: Дело, 2004

Дополнительная литература:

1. Башарин Г.П. Начала финансовой математики. – М.: ИНФРА-М, 1997.

2. Белов Б.А., Самаров К.Л., Щиканов А.Ю. Математика, экономико-математические методы и модели, финансовая

математика, эконометрика. Контрольные задания и методические указания. – М.: МГУС, 2004.

3. Капитоненко В.В. Финансовая математика и ее приложения. – М.: Приор, 1998.

4. Кочович Е. Финансовая математика. Теория и практика финансово-банковских расчетов. – М.: Финансы и статистика, 1994.

5. Ковалев В.В., Уланов В.А. Курс финансовых вычислений. – М.: Финансы и статистика, 1999.

6. Кутуков В.Б. Основы финансовой и страховой математики. – М.: Дело, 1998.

7. Малыхин В.И. Финансовая математика. Учебное пособие. – М.: ЮНИТИ-ДАНА, 2000.

8. Мелкумов Я.С. Финансовые вычисления. Теория и практика. Учебно-справочное пособие. – М.: ИНФРА-М, 2002.

9. Четыркин Е.М. Методы финансовых и коммерческих расчетов. – М.: Дело, 1995.

10. Четыркин Е.М. Финансовая математика. Учебник. – М.: Дело, 2002.

Составители: Чеховская Ирина Александровна,

Харламова Екатерина Евгеньевна

Методические указания «Методы финансовых расчетов (для студентов, обучающихся по направлениям подготовки «Экономика» и «Менеджмент»)

Темплан 2014. Поз. №

Подписано в печать 2014. Формат 60×84 1/16.

Бумага газетная. Печать офсетная. Усл. печ. л. .

Тираж 100 экз. Заказ____. Бесплатно.

Волгоградский государственный технический университет.

400005 Волгоград, просп. им. В. И. Ленина, 28.

РПК «Политехник» Волгоградского государственного технического университета.

400005 Волгоград, ул. Советская, 35.