Метод внутренней нормы прибыли проекта (IRR, ВНД)
Внутренняя норма прибыли (внутренняя норма доходности) – обычно это такое положительное число R, что при норме дисконта r = R NPV проекта обращается в 0.
Таким образом, чтобы найти значение внутренней нормы прибыли проекта, необходимо решить уравнение вида 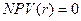 относительно r.
относительно r.
Экономический смысл показателя IRR при анализе эффективности инвестиций заключается в следующем: внутренняя норма доходности показывает максимально допустимый относительный уровень расходов, которые могут быть ассоциированы с данным проектом. Например, если проект полностью финансируется за счет кредита коммерческого банка, то значение IRR показывает верхнюю границу допустимого уровня банковской процентной ставки, превышение которого делает проект убыточным.
Для оценки эффективности проекта значение IRR необходимо сопоставить с нормой дисконта r. Проекты, у которых 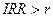 , имеют положительное NPV и поэтому эффективны. А те, которых
, имеют положительное NPV и поэтому эффективны. А те, которых 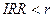 , имеют отрицательное NPV и поэтому неэффективны.
, имеют отрицательное NPV и поэтому неэффективны.
IRR может быть использована также для:
· оценки эффективности проекта, если известны приемлемые значения IRR (зависящие от области применения) у проектов различного типа;
· оценки степени устойчивости проекта (по разности 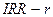 );
);
· установления участниками проекта нормы дисконта r по данным об IRR альтернативных направлений вложения ими собственных средств.
На практике расчет IRR удобнее всего вести с помощью компьютерных программ, т. е. путем перебора значений r определить R, при которой NPV обращается в 0.
Приближенное значение IRR можно получить путем расчета методом интерполяции. Для расчета необходимо два значения NPV, наиболее близко лежащие к нулю: одно – минимальное положительное значение, второе – максимальное отрицательное значение, а также соответствующие каждому из NPV нормы дисконта:
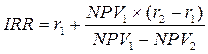 |
где 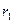 – норма дисконта, при которой NPV> 0;
– норма дисконта, при которой NPV> 0;
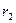 – норма дисконта, при которой NPV< 0;
– норма дисконта, при которой NPV< 0;
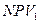 – положительное значение NPV при норме дисконта
– положительное значение NPV при норме дисконта 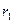 ;
;
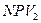 – отрицательное значение NPV при норме дисконта
– отрицательное значение NPV при норме дисконта 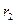 .
.
Недостатком метода IRR является то, что уравнение 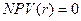 необязательно имеет один положительный корень. Оно может вообще не иметь корней (1) или иметь несколько положительных корней (2).
необязательно имеет один положительный корень. Оно может вообще не иметь корней (1) или иметь несколько положительных корней (2).
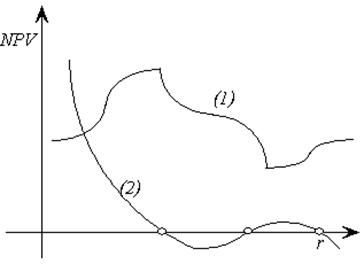
Зависимость NPV от нормы дисконта
Для того, чтобы преодолеть эти трудности, лучше определять IRR иначе:
IRR – это положительное число R такое, что NPV: · при норме дисконта 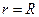 обращается в 0; · при всех обращается в 0; · при всех 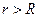 отрицательна; · при всех отрицательна; · при всех 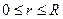 положительна. положительна. |
Другим недостатком метода IRR, является то, что различные ряды денежного потока могут создавать одинаковую IRR. Кроме того, он может противоречить результатам метода NPV.
Полезным инструментом в принятии инвестиционных решений является теория решений, то есть аналитический подход к выбору лучшей альтернативы или курса действий. Это подход может быть использован для учета риска при выборе того или иного варианта осуществления ИП.
В теории решений можно выделить три типа рассматриваемых проблем, отличающихся степенью определенности возможных результатов или последствий:
1) Принятие решений в условияхопределенности(наличия полной информации) – т. е. принимающий решение знает определенно результаты и последствия любой альтернативы или выбора.
2) Принятие решений в условиях неопределенности (отсутствие информации, полное "незнание") – принимающий решений не знает вероятности получения результатов при каждом выборе.
3) Принятие решений в условиях риска(неполной информации) – принимающий решение знает вероятность получения результатов или последствий для каждого выбора.
Принятие решений в условиях определенности – самая легкая ситуация, с которой может столкнуться менеджер. Здесь достаточно определить стоимость каждого альтернативного инвестиционного решения и выбрать проект с более высокой отдачей.
В условиях неопределенности,когда полностью неизвестно, какими будут обстоятельства, возможно использование трех методов принятия решений:
1) Максимакс (правило Вальда) – максимизация максимальных результатов для каждой альтернативы. Сначала мы ищем максимальный результат для каждой альтернативы, затем выбираем альтернативу с максимальным значением. Этот критерий решений называют оптимистическим, т.к. он ориентирован на наивысший результат и соответствует поведению удачливого игрока.
2)Максимин – максимизация минимальных результатов для каждой альтернативы. Сначала мы находим минимальные результаты внутри каждой альтернативы, а затем выбираем альтернативу с максимальным значением. Так как здесь выбирается альтернатива с наименьшими возможными убытками, критерий решения называется пессимистическим. Этот критерий подходит для ситуаций, описываемых теорией игр, т.е. при существовании рационального действующего противника, который хотел бы оказать негативное влияние на результат субъекта решений, но не подходит для безразличного, невраждебного окружения.
3) Равновероятный подход(правило Лапласа, правило недостаточной причины) – максимизация средних результатов для каждой альтернативы. Сначала мы подсчитываем средний результат для каждой альтернативы (делением суммы всех результатов на число результатов). Затем мы выбираем альтернативу с максимальным средним результатом. Равновероятный подход предполагает, что каждый вариант обстоятельств имеет одинаковую вероятность случиться.
Принятие инвестиционных решений в условиях риска полагается на принцип математического ожидания (принцип Байеса), в основе которого лежит оценка вероятностей реализации каждой из возможных ситуаций. При помощи таблицы с условными стоимостями каждого решения и оценками вероятностей каждого типа обстоятельств, мы определяем математическое ожидание каждой альтернативы. Выбор альтернативы с максимальным значением математического ожидания – один из наиболее популярных критериев решения.
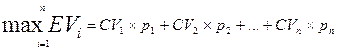 |
где 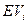 – математическое ожидание i-той альтернативы;
– математическое ожидание i-той альтернативы;
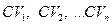 – условная стоимость i-той альтернативы при обстоятельствах 1, 2 ...n;
– условная стоимость i-той альтернативы при обстоятельствах 1, 2 ...n;
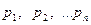 – вероятность осуществления обстоятельств 1, 2 ...n.
– вероятность осуществления обстоятельств 1, 2 ...n.
