Методика 2 расчета нетто-ставки по массовым рисковым видам страхования
Страховой компании требуется рассчитать тарифную ставку по имущественному виду страхования на 0006 год, исходя из данных, приведенных в Таблице 3.
Таблица 3 – Оценка страхового возмещения и страховых сумм за период 0001-05 годы
| Годы | Общая страховая сумма S, тыс. руб. | Страховое возмещение Sb, тыс. руб. | Фактическая убыточность 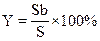 |
| 260+196=456 | 0.456 | ||
| 340+104=444 | 0.444 | ||
| 370+106=476 | 0.476 | ||
| 215+718=933 | 0.933 | ||
| 25+125=150 | 0.15 |
Необходимо найти прогнозируемый уровень убыточности страховой суммы, для чего используем модель линейного тренда, согласно которой фактические данные по убыточности страховой суммы выравниваются на основе линейного уравнения:
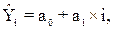 (10)
(10)
где 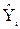 – выровненный показатель убыточности страховой суммы;
– выровненный показатель убыточности страховой суммы;
а0, а1 – параметры линейного тренда,
i – порядковый номер соответствующего года.
Найдем параметры а0 и а1 уравнения линейного тренда, для чего решим систему уравнений:
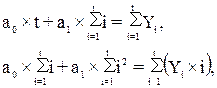 (11)
(11)
где t – число анализируемых лет,
Yi – фактическая убыточность страховой суммы по i-му риску.
Коэффициенты данной системы уравнений находятся с помощью Таблицы 4.
Таблица 4 – Расчетные показатели для нахождения уравнения тренда
| Годы | i | Фактическая убыточность Yi | Расчетные показатели | |
| Yi * i | i 2 | |||
| 0,456 | 0,456 | |||
| 0,444 | 0,888 | |||
| 0,476 | 1,428 | |||
| 0,933 | 3,732 | |||
| 0,15 | 0,75 | |||
| Сумма | 2,459 | 7,254 |
Подставив полученные в Таблице 4 данные с систему уравнений (11), получим:
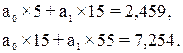
Решив систему уравнений, получаем следующие значения:
а0 = 0,5287 и а1 = -0,0123.
На основании найденных значений определим выровненную убыточность по годам, подставляя данные в уравнение (10).
Найдем ожидаемую убыточность на 0006 год с учетом тренда исходных данных:
Y0006 = 0,5287 – 0,0123*6 = 0,4549 (руб.) со 100 рублей страховой суммы, – это и есть основная часть нетто-ставки.
Для определения величины рисковой надбавки необходимо рассчитать ряд вспомогательных значений, которые представлены в Таблице 5.
Таблица 5 – Данные для расчета среднеквадратического отклонения убыточности страховых сумм
| Годы | i | Фактическая убыточность Yi | Выровненная убыточность 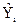 | Отклонения выровненной убыточности от фактической ( 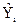 -Yi ) -Yi ) | Квадраты отклонений ( 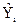 -Yi )2 -Yi )2 |
| 0,456 | 0,5164 | + 0,0604 | 0,003648 | ||
| 0,444 | 0,5041 | + 0,0601 | 0,003612 | ||
| 0,476 | 0,4918 | + 0,0158 | 0,000249 | ||
| 0,933 | 0,4795 | - 0,4535 | 0,205662 | ||
| 0,15 | 0,4672 | + 0,3172 | 0,100615 | ||
| Сумма | 0,313786 |
Для определения рисковой надбавки необходимо рассчитать среднеквадратическое отклонение σ фактических значений убыточности от выровненных значений:
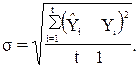 (12)
(12)
Подставив рассчитанные показатели в формулу (12), получим:
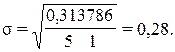
Нетто-ставка Tn рассчитывается следующим образом:
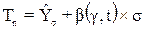 , (13)
, (13)
где 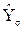 – выровненная убыточность в году, для которого рассчитывается тарифная ставка,
– выровненная убыточность в году, для которого рассчитывается тарифная ставка,
β(γ,t) – коэффициент, используемый для исчисления размера рисковой надбавки. Величина зависит от заданной гарантии безопасности γ (той вероятности, с которой собранных взносов хватит на выплаты страховых возмещений) и t – числа анализируемых лет и может быть взята из Таблицы 6.
Таблица 6 – Зависимость коэффициента β от задаваемой гарантии безопасности и числа анализируемых лет
| t | γ | ||||
| 0,8 | 0,9 | 0,95 | 0,975 | 0,99 | |
| 2,972 | 6,649 | 13,640 | 27,448 | 69,740 | |
| 1,592 | 2,829 | 4,380 | 6,455 | 10,448 | |
| 1,184 | 1,984 | 2,850 | 3,854 | 5,500 | |
| 0,980 | 1,596 | 2,219 | 2,889 | 3,900 |
γ = 0,95, t = 5, тогда β = 2,850.
Нетто-ставка со 100 рублей страховой суммы составит:
Tn = 0,4549 + 2,850 * 0,28 = 1,2529 (руб.).
Брутто-ставка Т определяется по следующей формуле (9).
Брутто-ставка страхового тарифа рассчитывается из условия, что нагрузка определена страховой организацией в размере 20% от брутто-ставки:
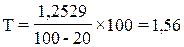 (руб.).
(руб.).
Таким образом, согласно представленной методики, страховая организация установит тарифную ставку на 0006 год в размере 1,56 руб. со 100 рублей страховой суммы.
