Анализ данных с помощью команд Подбор параметра и Поиск решения

Команда Сервис→Подбор параметра используется для получения такого значения аргумента некоторой функции, при котором функция принимает заданное значение. Так как реализацию этой команды Excel выполняет численным методом (методом последовательных приближений Ньютона), необходимо задать начальное значение аргумента (первое приближение к искомому значению). Для вызова команды следует:

§ выбрать ячейку, содержащую формулу (функцию искомого аргумента),

§ выбрать вкладку Данные, панель инструментов Работа с данными → Анализ «что если» →Подбор параметра и в диалоговом окне Подбор параметра задать

o начальное значение аргумента,

o искомое значение функции.

Метод подбора параметров используется, например, для нахождения корней уравнения.

Вкладка Данные, команда Поиск решения используется для решения системы уравнений с несколькими неизвестными или уравнения с несколькими переменными и заданными ограничениями на решения. Чаще всего эта команда используется для решения линейной и нелинейной задачи оптимизации.

Для установки предельного числа итераций и относительной погрешности вычислений следует использовать вкладку Вычисления диалогового окна команды Сервис→Параметры. По умолчанию Excel предлагает предельное число итераций – 1000 и относительную погрешность – 0,001.

Содержание работы

Задания выполняйте на отдельных листах созданной Вами книги.

Задание 1. Табулирование функций и построение графиков функций

Назовите новый рабочий лист График.

Постройте график функции1 y=Sin(x³) в интервале от -1 до 1 с шагом 0,1. Тип диаграммы выберите Точечная или График. При редактировании графика задайте заголовки, убедитесь, что подписи по оси x соответствуют табличным значениям. На том же графике отобразите функцию 2 y=cos(x³)+x (выберите график функции 1, в контекстном меню активизируйте Исходные данные и на вкладке Ряд добавьте график, указав диапазон ячеек со значениями функции 2 в поле Значения.

Задание 2. Построение трехмерных графиков

Создайте новый лист с именем Поверхность. Постройте график поверхности в соответствии с заданием. Выберите ориентацию графика, соответствующую наиболее наглядному представлению поверхности.

Задание 3. Работа с массивами. Решение системы линейных алгебраических уравнений (СЛАУ)

СЛАУ в матричной форме имеет вид Ax = b, где A – матрица коэффициентов, x – вектор неизвестных, b ‑ вектор свободных членов:

, , .

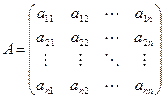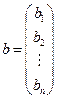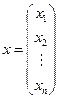Решение системы уравнений в матричном виде: x = A^-1b,

Где A^-1 –матрица,обратная к матрицеА. Для проведения вычислений следует:

§ ввести исходные матрицу и векторы,

§ построить обратную матрицу (выделить диапазон ячеек для хранения обратной матрицы (размер диапазона должен совпадать с размером массива А) и вызвать функцию МОБР. Для запуска функции следует воспользоваться комбинацией клавиш [Ctrl+Shift+Enter];

§ выделить массив для результата и вызвать функцию МУМНОЖ;

§ в диалоговом окне задать исходные массивы ‑ диапазоны ячеек с матрицей A^-1и вектором b.Для запуска функции также следует нажать [Ctrl+Shift+Enter].

Задача. Найти решение системы линейных уравнений:

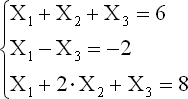Создайте новый лист с именем СЛАУ и выполните на нем вычисление заданной системы матричным методом.

Задание 5. Подбор параметра при выполнении финансовых расчетов

Методом подбора параметра рассчитать, при какой ежемесячной процентной ставке С можно за год накопить S рублей, внося каждый месяц платеж на n % больше предыдущего, начав с первого платежа P рублей.

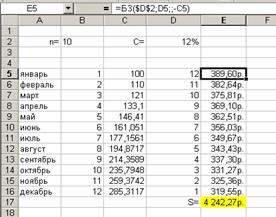Слева представлено заполнение таблицы для расчета накопления за год при процентной ставке C=12% годовых, n=10% и P=100 руб.

Применяемые формулы:

§ в ячейке C6: =C5+С5*0,1;

§ в ячейке E5: =БС($D$2;D5;;-C5);

§ в ячейке E17: =СУММ(E5:E16).

Финансовая функция БС возвращает будущее значение вклада на основе периодических постоянных платежей и постоянной процентной ставки.

Синтаксис: БС(ставка; кпер; плата; нз; тип),

где

§ ставка – процентная ставка или скидка по вложению или ссуде за период выплат,

§ кпер – общее количество платежей или периодов выплат (это значение в примере уменьшается на 1 каждый месяц),

§ плата– объем периодической выплаты по вложению или ссуде (в примере =0),

§ нз – общая сумма, которую составят будущие платежи, начиная с текущего момента (в примере это сумма, которую следует вернуть (=0), минус сумма начального вложения);

§ тип – режим выплат, с которым осуществляются выплаты (значение 0 соответствует выплатам в конце месяца, значение 1 ‑ в начале месяца).

Для расчета накопления, например 7000 рублей, вызывается команда Подбор параметра для формулы в ячейке Е17 (общая сумма выплаты) и задается изменяемая ячейка D2 (ежемесячная процентная ставка).

Выполните расчеты для заданных преподавателем значений S, n, P и C.

Задание 7. Решение оптимизационной задачи

Для решения оптимизационных задач предназначено средство Поиск решения.

Пусть необходимо найти максимум функции Z(x), где

,

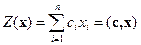с – заданный вектор, x – искомый вектор

при ограничениях A x ≤ b, где А – матрица размером m×n; b=(b₁,b₂,…,b_m).

Функция Z называется целевой функцией. Так как целевая функция и ограничения линейно зависят от переменных, оптимизационная задача в такой постановке называется задачей линейного программирования.

Пример поиска максимума функции Z=3000x₁+2000x₂ при ограничениях:

x₂+2x₁≤6,

2x₁+x₂≤8,

x₂-x₁≤1,

x₂≤2,

x₁,x₂≥0.

Ниже на рисунке а) представлено окно с вводимыми формулами. Для искомых значений x1 и x2 зарезервированы ячейки A3 и B3.

После ввода формул выделяется ячейка, содержащая целевую функцию (С4) и вызывается команда Сервис→Поиск решения. Окно команды с введенными ограничениями представлено на рисунке б).

Результат поиска решения представлен на рисунке в).

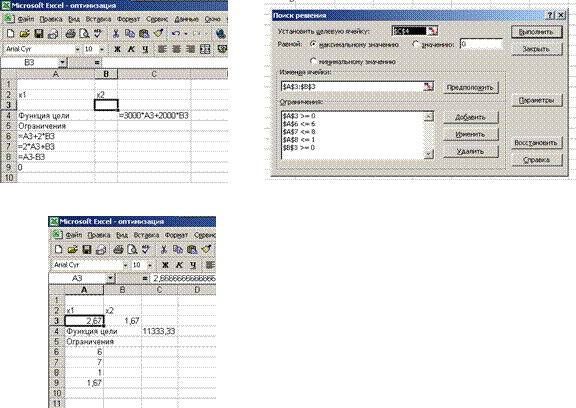
a) б)

в)

Пример решения оптимизационной задачи

Выполните решение оптимизационной задачи в соответствии с заданием преподавателя. Выделите на листе результаты расчетов. Убедитесь, что найденное решение не противоречит заданным ограничениям.

Контрольные вопросы и задания

1. Какие типы диаграмм Excel можно применять для построения графиков функций?

2. Чем различаются диаграммы типа График и Точечная?

3. Как метод работы с массивами применяется для решения системы линейных уравнений?

4. Следует ли учитывать работу с массивами при решении СЛАУ методом Крамера?

5. Какой численный метод лежит в основе выполнения команды Подбор параметра?

6. Что представляют собой оптимизационные задачи?

7. В каких случаях решается задача линейного программирования?

8. Как применить команду Поиск решения для решения задачи оптимизации?

9. Какая из команд – Поиск решения или Подбор параметра – может быть применена для решения нелинейного уравнения?

Лабораторная работа № 9