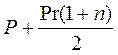Типовые задачи с решениями. Пусть заем в сумме Р выдан под r простых ссудных процентов на n периодов
Пусть заем в сумме Р выдан под r простых ссудных процентов на n периодов. К концу финансовой операции величина займа составит величину
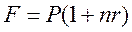 .
.
Если предполагается возвращать займ одним платежом в конце срока финансовой операции, то величина F и есть размер возвращаемого платежа.
Задача 1. Погашение займа одним платежом.
Ссуда в сумме 5 млн. руб. выдана на 5 лет под 10% годовых. Определить размер платежа, если ссуда возвращается одним платежом в конце срока финансовой операции и начисляются простые проценты.
Решение
Величину платежа находим по формуле
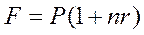 при Р=5; r = 0,1; n =5:
при Р=5; r = 0,1; n =5:
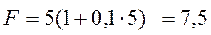
Размер платежа равен 7 500 000 руб.
Пусть заем в сумме Р выдан под r сложных ссудных процентов на n периодов. К концу финансовой операции величина займа составит величину
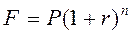 .
.
Если предполагается возвращать займ одним платежом в конце срока финансовой операции, то величина F и есть размер возвращаемого платежа.
Задача 2. Погашение займа одним платежом.
Ссуда в сумме 5 млн. руб. выдана на 5 лет под 10% годовых. Определить размер платежа, если ссуда возвращается одним платежом в конце срока финансовой операции и начисляются сложные проценты.
Решение
Величину платежа находим по формуле
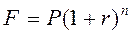 при Р=5; r = 0,1; n =5:
при Р=5; r = 0,1; n =5:
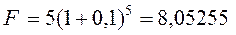
Размер платежа равен 8 052 550 руб.
Сам заем называется основным долгом, а наращиваемый добавок –процентными деньгами. Пусть заем в сумме Р выдан под r сложных ссудных процентов на n периодов. За первый год процентные деньги составят величину r×P. Если эти деньги выплатить, то останется только основной долг в размере Р. Таким же образом в конце каждого года (кроме последнего) выплачивается одна и та же величина r×P. В конце n-ного, последнего года, выплаты составят величину r×P+Р, процентные деньги и сумму основного долга.
Общая сумма выплат за n периодов составит величину Р+ r×P×n=P(1+nr), т.е. операция погашения займа способом погашения основного долга одним платежом в конце эквивалентна наращению долга по схеме простых процентов по ставке r.
Задача 3. Погашение основного долга одним платежом.
Ссуда в сумме 5 млн. руб. выдана на 5 лет под 10% годовых. Определить общую сумму выплат, если ссуда возвращается способом «погашение основного долга одним платежом в конце срока финансовой операции».
Решение
Величина процентных платежей за 8 лет составит r×P×n=0,1×5×5=2,5
Общая сумма выплат составит 2,5 млн.+ 5 млн. =7,5 млн.руб.
Пусть заем в сумме Р выдан под r сложных ссудных процентов на n периодов. При погашении основного долга равными годовыми выплатами в конце каждого года выплачивается n-ная доля основного долга и проценты, начисленные на сумму долга, которой пользовались в течение года.
В конце первого года выплачивается доля основного долга, равная величине P/n и выплачиваются проценты с суммы Р, которой пользовались в течение года, равные величине r×P. Общий платеж в конце первого года равен величине P/n+ r×P.
В конце второго года выплачивается доля основного долга, равная величине P/n и выплачиваются проценты с суммы (Р- P/n), которой пользовались в течение года, равные величине r× (Р- P/n). Общий платеж в конце второго года равен величине P/n+ r× (Р- P/n).
В общем случае в конце года k+1 общий платеж равен величине P/n+ r× (Р- k×P/n).
Платежи каждого года образуют арифметическую прогрессию с разностью
d=r×P/n, первым членом a1 =P/n+ r×P и последним членом an =P/n+ r×P/n.
Сумма n членов арифметической прогрессии равна
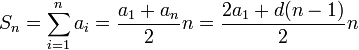
Величина выплат составит