Оценка премии за риск. Модель оценки долгосрочных активов

Предложены различные модели обоснования повышенной доходности за риск инвестирования, прежде всего в ценные бумаги (asset princing models). Наиболее успешные модели находятся посередине между двумя крайними позициями — "абсолютного" определения цены риска на основе функций полезности и "относительного" — что можно сказать о цене данного актива с учетом риска, если известна цена на другие активы (например, модель цены опциона Блэка — Шоулса).

Наибольшее признание получила разработанная в середине 1960-х гг. модель оценки долгосрочных активов (capital asset princing model – CAPM). Модель утверждает, что на конкурентных рынках капитала в состоянии равновесия (когда все ценные бумаги и активы оцениваются рынком верно) премия за риск инвестирования в актив находится в прямой зависимости от чувствительности этого актива к движению рынка (т.е. от βj):

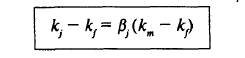
где (кт – к) — рыночная премия за риск.

Эта зависимость риска и доходности по конкретному активу j

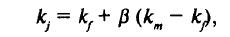
представленная графически, носит название рыночной линии ценной бумаги (security market line - SML). Зависимость показана на рис. 3.17. По оси абсцисс откладывается оценка риска (β-коэффициент), по оси ординат — требуемая доходность инвестора с учетом риска. Для безрискового актива β-коэффициент равен нулю и требуемая доходность совпадает с безрисковой доходностью.

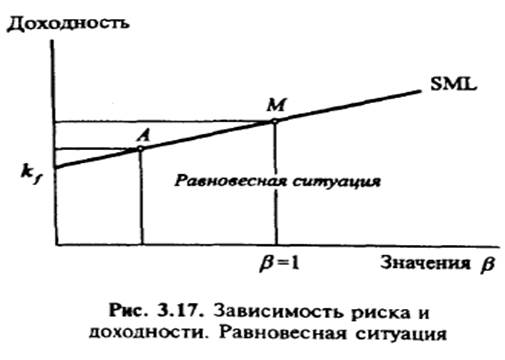
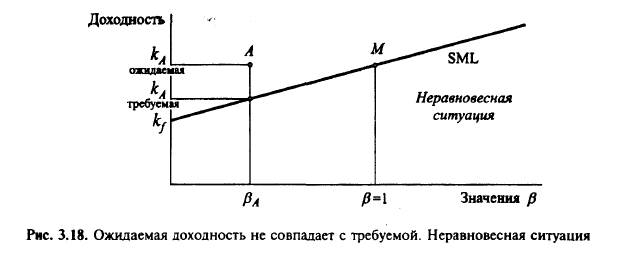
Прямая SML на рис. 3.17 отражает выбор среднего инвестора в равновесии (инвестору нет необходимости продавать или покупать данные акции), когда требуемая доходность по акции (или рисковому активу) равна ожидаемой доходности. Если для инвестора прямая SML выглядит как на рис. 3.18 и ожидаемая доходность по акции А превышает требуемую данным инвестором, то он предпочтет приобрести большее количество акций А.

Если большое число инвесторов сочтут, что акции А недооценены (цена низка, и ожидаемая доходность высока), то повышение спроса на акции А вызовет рост цены, что приведет к падению ожидаемой доходности. Покупка акций А прекратится, когда ожидаемая доходность сравняется с требуемой и установится равновесие. Это равновесие и отражает прямая SML, изображенная на рис. 3.18.

Таким образом, равновесное состояние на рынке складывается в результате корректировки инвесторами структуры индивидуальных портфелей и давления через спрос и предложение на курсы ценных бумаг. Располагая информацией о курсах ценных бумаг, инвесторы имеют возможность рассчитать ожидаемые доходности по ним и коэффициенты корреляции. Подход САРМ позволяет рассчитать требуемую доходность. До тех пор пока ожидаемая доходность не сравняется с требуемой, общий спрос на конкретную ценную бумагу не совпадет с предложением, что отразится на движении цены. Наклон прямой SML отражает отношение к риску на данном рынке (в данной экономике), так как показывает выбор среднего инвестора. Чем меньше среднерыночный инвестор склонен к риску, т.е. чем больше угол наклона прямой SML, тем:

• больше премия за риск по любому рисковому активу (в том числе по всем акциям);

• выше требуемая доходность по всем рисковым активам.

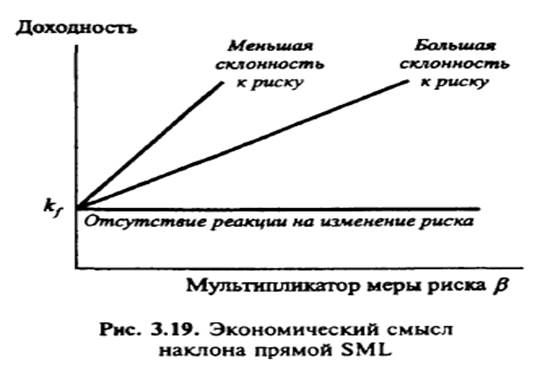
Различные отношения к риску в экономике показаны тремя прямыми SML на рис. 3.19. Чем больше риск, тем больше в общем случае премия за риск. При меньшей склонности к риску инвестор требует большую премию за фиксированный уровень риска β*(k2 > k1)

Факторы, оказывающие влияние на положение прямой SML

1. Влияние инфляции. Безрисковая доходность в САРМ является номинальной, т.е. включает две составляющие: реальную безрисковую доходность (ставку процента) и ожидаемую инфляцию. При росте ожидаемой инфляции номинальная безрисковая доходность растет, что приводит к изменению положения прямой SML как показано на рис. 3.20 (сдвиг прямой SML вверх по оси ординат).

2. Изменение склонности к риску. Фактор изменения отношения к риску меняет наклон прямой SML. Рис. 3.21 показывает изменение положения SML при возрастании неприятия риска.

Возрастает рыночная премия за риск (kт — kf), что приводит к росту требуемой рыночной доходности с kт1 до kт 2.

Требуемая доходность по другим рискованным ценным бумагам и портфелям также растет, но с учетом степени влияния систематического риска (чем меньше оценка систематического риска —значение Д-коэффициента, тем меньше будет рост требуемой доходности).

3. Изменение β-коэффициента. Корпорация может менять меру систематического риска (^-коэффициент) через:

комбинацию реальных активов;

изменение доли заемного капитала в общем капитале.

Кроме того, β-коэффициент подвержен влиянию внешних факторов, таких, как изменение конкурентного состояния отрасли, ограничения по производству со стороны государства. Все эти изменения отражаются на изменении требуемой доходности.

Модель, описываемая уравнением kj = kr + β (km – kf) для актива j, строится на следующих предположениях:

1) все инвесторы максимизируют свою ожидаемую полезность и с этой целью осуществляют инвестиции в активы;

2) не рассматривается динамика принятия решений, учитывается только один период, одинаковый для всех инвесторов;

3) выбор из альтернативных вариантов инвестирования осуществляется по соотношению ожидаемой доходности и риска (измеряемого стандартным отклонением);

4) инвесторы — противники риска;

5) все инвесторы владеют одинаковой информацией о вероятностном распределении ожидаемой доходности по активам, и вероятностное распределение является нормальным;

6) на рынке имеются неограниченные возможности инвестирования и займа денег по единой безрисковой процентной ставке;

7) отсутствуют трансакционные издержки обращения активов;

8) дивидендные выплаты и прирост капитала облагаются налогами одинаково;

9) на рынке отсутствует возможность влияния на рыночную цену актива отдельными инвесторами через большой объем сделок;

10) все активы высоколиквидны и бесконечно делимы. Инвестор может купить часть акции.

Уравнение SML по активу j : kj = kf + β (km – kf) утверждает, что требуемая (и соответственно в равновесии ожидаемая) доходность актива j включает две компоненты: доходность безрискового актива и премию за риск. Премия за риск инвестирования в активы зависит от: 1) премии за риск рыночного портфеля (по этому портфелю, состоящему из всех активов рынка, β =1 и премия равна km – kf; 2) значения β-коэффициента по рассматриваемому активу j. Если β = 1, то требуемая доходность по активу j совпадает со средней доходностью по всем активам, т.е. равна доходности рыночного портфеля. Если βj > 1, то премия за риск по активу у выше рыночной премии за риск на множитель β и соответственно выше общая требуемая доходность.

Для оценки требуемой доходности по САРМ необходима следующая информация: безрисковая доходность; премия за риск рыночного портфеля; по активу./р.

Если информация доступна, то можно по SML оценить требуемую доходность. Например, по акциям компании "Британские авиалинии" значение β на октябрь 1994 г. было 1,31, доходность по трехмесячным казначейским векселям составляла на тот момент 6,5%, доходность лондонского фондового рынка — 13,5% . Доходность по SML на октябрь 1994 г. составит 15,7% (6,5% + 1,31 х 7%) = 15,7%).

? С А Р М часто используется для оценки деятельности профессиональных участников фондового рынка. Предположим, что пенсионный фонд обеспечивал среднегодовую доходность 24%. Р портфеля = 1,5.

Фондовый индекс возрастал ежегодно за рассматриваемый период времени на 20%. Безрисковая доходность принимается на уровне 10 % в год. Управляющий фондом утверждает, что он обеспечил более высокую доходность по сравнению с рынком. Действительно ли менеджер переиграл рынок на 4 процентных пункта и пригодна ли модель САРМ для описания соотношения риска и доходности?

Рыночная модель и САРМ

Рыночная модель, описываемая уравнением kj = αj + βjkm + u, и САРМ, описываемая уравнением kj = kf + β (km – kf), являются однофакторными моделями оценки требуемой доходности по ценной бумаге. Отличие этих моделей состоит в следующем:

1) в рыночной модели фактором является рыночный (фондовый) индекс, а в САРМ — рыночный портфель, который охватывает большее количество рисковых финансовых активов, чем рыночные индексы;

2) рыночная модель в отличие от САРМ не является равновесной;

3) теоретически β-коэффициент рыночной модели не совпадает с 0-коэффициентом САРМ (в рыночной модели он отражает чувствительность к рыночному индексу, а в САРМ — к изменению рыночного портфеля). Однако из-за невозможности оценить β-коэффициент по отношению к рыночному портфелю в САРМ на практике используется β-коэффициент из рыночной модели.