Будущая стоимость единицы (накопленная сумма единицы)
Временная оценка денежных потоков
Стоимость собственности, приносящей доход, определяется текущей стоимостью денежных потоков, которые ожидается получать в различные периоды времени в будущем.
Временная теория стоимости денег исходит из предположения, что деньги, являясь товаром, со временем меняют свою стоимость и, как правило, обесцениваются. Изменения со временем стоимости денег происходят под влиянием целого ряда факторов. Важнейшими факторами можно назвать инфляцию и способность денег приносить доход при условии их разумного инвестирования в альтернативные проекты. Следует особо подчеркнуть, что денежные суммы имеют неодинаковую стоимость во времени даже в отсутствие инфляции. Например, сегодняшняя ценность 10 тысячи тенге которая лежит у вас в бумажнике, и 10 тысячи тенге, которая будет вам выплачена в виде заработной платы через 1 месяц, неодинакова, хотя номинально суммы равны. Имеющуюся тысячу вы можете сегодня поместить на срочный депозит в банк (или инвестировать в любой приносящий доход актив) и спустя месяц получить доход от процентов, скажем, 500 тенге. Отсюда важное правило: чем дальше в будущем отстоят от нас предполагаемые денежные суммы, тем меньше их сегодняшняя ценность. Для правильного и точного определения стоимости денег во времени необходимо учитывать ряд факторов: (1) номинальные денежные суммы; (2) сроки инвестирования (накопления дохода); (3) периодичность начисления процентов (дохода); (4) ставку дохода (ее могут называть ставкой или нормой процента, а также ставкой или нормой дисконтирования – это все синонимы).
Будущая стоимость единицы (накопленная сумма единицы)
Данная функция позволяет определить будущую стоимость суммы, которой располагает инвестор в настоящий момент, исходя из предполагаемой ставки дохода, срока накопления и периодичности начисления процентов. Различают технику простого и сложного процента.
Простой процент начисляется только один раз в конце срока депозитного договора.
Пример:
Вклад в 10.000 долл. внесен на счет под 12% годовых. Какая сумма будет на счете к концу второго года?
10.000*(1+0,12*2)=12,400
Сложный процент предполагает начисление процентов не только на сумму первоначального взноса, но и на сумму процентов, накопленных к концу каждого периода.
Рассмотрим процесс накопления в динамике.
| Год | Накопленная сумма (долл.) |
| 1. | 10.000*112%=11.200 |
| 2. | 11.200*112%=12.544 |
Базовая формула для расчета будущей стоимости:
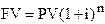
где
FV - будущая стоимость (стоимость в какой-то определенный момент времени в будущем);
PV - текущая стоимость (стоимость на сегодняшний день; в практическом смысле – на дату оценки)
i - ставка процента
n - число периодов начисления процентов
При PV=1, формула имеет вид: 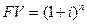
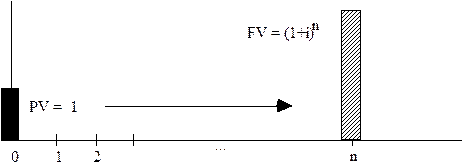
На данном рисунке показана известная нам величина текущей стоимости PV=1, горизонтальная ось изображает срок накопления денежных сумм, а на момент времени n показана неизвестная нам будущая стоимость FV, которую можно определить по указанной формуле.
Поскольку сложный процент применяется очень часто и широко, были разработаны стандартные таблицы, содержащие предварительно рассчитанные факторы сложного процента. Фактором называется число, которое, будучи перемноженным на заданное число, дает искомый результат. В таблице факторы будущей стоимости показаны в колонке 1.
Более частое начисление процента.
Нередко период накопления короче года. Начисление процентов может происходить раз в полгода, в квартал, раз в месяц и т. д. В данном случае необходима корректировка базовой формулы будущей стоимости. При корректировке число лет, на протяжении которых происходит накопление, умножается на частоту начисления процентов в течение одного года, а номинальная ставка процента делится на частоту начисления.
FV=PV*(1+i/m)n*m, где
m - частота начисления процента
Пример:
На вклад в 10.000 долл. процент начисляется раз в квартал. Годовая ставка процента равна 12. Какая сумма будет на счете в конце второго года?
10.000*(1+0,12/4)2*4=10.000*1,2668=12.668
Вопросы для контроля
1. Стоимость земельного участка, купленного за 20.000 долл., повышается на 15% в год (по сложному проценту). Сколько он будет стоить через пять лет?
Ответ:
20.000*2,011357=40.227,14
Текущая стоимость единицы
Текущая стоимость единицы – это величина, обратная накопленной сумме единицы. Это сегодняшняя стоимость единицы, которая должна быть получена в будущем.
Процесс определения текущей стоимости единицы (его также называют дисконтированием; не путать с дисконтом – скидкой!) аналогичен процессу накопления дохода от процентов, но имеет обратную направленность во времени: от будущего к настоящему. То есть мы определяем, сколько нужно сегодня вложить в приносящий периодический доход от процентов актив, чтобы в конкретный момент времени в будущем получить заранее заданную сумму. При определении текущей стоимости ставку процента, по которой начисляется периодический доход, чаще называют ставкой дисконтирования.
Функция текущей стоимости единицы дает возможность определить стоимость суммы в данный момент, если известна ее величина в будущем, число периодов и ставка процента.
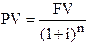
где
PV - текущая стоимость;
FV - будущая стоимость;
i - ставка процента (ставка дисконтирования)
n - число периодов начисления процентов
Фактор текущей стоимости единицы в таблице показан в колонке 4.
При FV =1, формула имеет вид
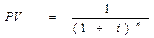 |

Данный рисунок иллюстрирует известную будущую стоимость FV=1 в момент времени n. Требуется определить неизвестную текущую стоимость PV в нулевой момент времени, то есть на сегодняшний день.
Пример:
При 10%-ой ставке процента текущая стоимость 100.000 долл., ожидаемых к получению через год, равна?
100.000*0,909091=90909,1
Проверка:
Если сегодня инвестор вкладывает 90909,1 долл. и в течение следующего года может получить чистый доход в 10%, т. е. 9090,91, то через год его капитал будет составлять 100.000 долл. (90909,1+9090,91)
Вопросы для контроля
3. Какую сумму следует сегодня депонировать в банке, начисляющем 12% годовых при ежемесячном накоплении, для того, чтобы через 4 года получить 10.000 долл.?
Ответ:
10.000*0,62026=6202,6
4. Сколько надо положить на счет в банке под 20% годовых, чтобы через десять лет купить квартиру за 120.000 долл.?
Ответ:
120.000*0,161506=19380,72
