Оценка облигаций. Купонные облигации

Облигация — это долгосрочное долговое обязательство, по которому эмитент (государство или корпорация) выплачивает держателю определенный процентный доход. Текущая оценка облигации (Р) есть сумма дисконтированных денежных потоков, обеспечиваемых этой ценной бумагой:

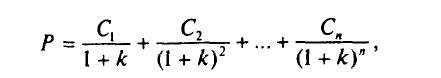
где k: — требуемая инвесторами доходность;

С — денежные потоки, прогнозируемые по облигации.

Цену Р и будущую выплату С разделяет один год.

Оценка облигаций должна учитывать периодичность получения денежных потоков, их величину и срок обращения. Так как облигации различаются по условиям получения денежного потока (срочные и бессрочные облигации, купонные и дисконтные, с плавающей и фиксированной купонной ставкой и др.), то используются различные модели определения цены и доходности.

Большинство корпоративных и часть государственных облигаций являются купонными (по ним ежегодно выплачивается фиксированный доход, а по окончании срока они погашаются по номиналу). Если купонные выплаты осуществляются раз в год, С – ежегодный купон, H — номинал, а срок обращения облигации — п лет, то цена Р купонной облигации находится как сумма текущих оценок (PV) всех платежей:

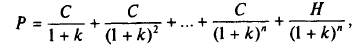
где k – требуемая инвесторами доходность.

Значение P может быть найдено тремя способами.

1. Прямое дисконтирование денежного потока каждого года, как показано на рис 4.1

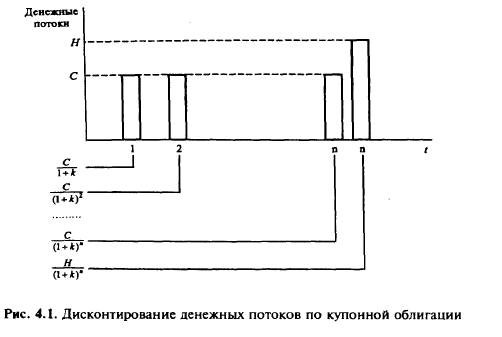
2. Табличное нахождение. Рис. 4.1 показывает, что платежи можно разделить на две части: серия из n равных периодических платежей (аннуитет), выплата номинала H в год n. Таким образом, цена Р облигации складывается из текущей оценки аннуитета с доходностью 1с и периодом получения выплат п — обозначим ее как РVанн (k, п) = РVIFA (k, п) (см. Приложение 1) — и текущей оценки номинала облигации:

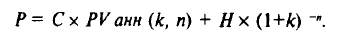
Например, для 10-летней купонной облигации с номиналом 1 тыс. долл. и ежегодной купонной выплатой 80 долл. при требуемой доходности 10% равновесная цена составит: Р= 80 х РVанн (10%, 10 лет) + 1000 (1 + 0,1)-10. Значение РVанн (k, п) находится из таблицы текущей оценки аннуитета в размере одной денежной единицы с заданными условиями k и п (табл. 2 Приложения 2).

Дисконтированное значение одной денежной единицы с условиями (k, п) также имеет табличное значение (табл. 1 Приложения 2). Отсюда Р= 80 х 6,1446 + 1000 х 0,3855 = 491,57 + 385,5 = 877,07 долл.

3. Программа Exel Мicrosoft — финансовая функция НПЗ (см. Приложение 3). В диалоговом режиме вводятся значения k %, С1, С2,..., Сл. Последнее значение отражает последний платеж (купонная выплата + номинал облигации). Итогом расчетов компьютера будет цена облигации. Например, для 3-летней облигации номиналом 1000 денежных единиц с купонной ставкой 10%, с одноразовыми выплатами в конце года и требуемой доходностью 15% НПЗ (15%, 100, 100, 1100) = 885,8387. Цена облигации на начало года равна 885,84 денежных единиц. Близкое значение дает табличное нахождение: 100 х РVIFА (3 года,15%) + 1000 х РVIFА (3 года,15%) = 100 х 2,2832 + 1000 х 0,6575 = 885,82.

По купонной облигации различают:

1) купонную ставку (coupon rate — СR) — ежегодную купонную выплату за каждую денежную единицу номинала, СR = С / Н;

2) текущую доходность, или процентную доходность (current yield — СY) — ежегодную купонную выплату на каждую денежную единицу текущей цены, СY = С/Р;

3) общую ожидаемую доходность за год (total yield — ТY) — сумму текущей доходности и доходности прироста капитала, ТY= (С + Рt + 1 - Р) / Рt = С / Р, + ( Р , + 1 – Рt) / Рt.

При равенстве купонной ставки общей ожидаемой доходности цена облигации равна номиналу. Так, в рассмотренном выше примере купонная ставка равна 8% (80 /1000 = 0,08), и если требуемая доходность на рынке также равна 8%, то текущая рыночная цена составит 1 тыс. долл.: 1000 = 80 х х РV анн (8%, 10 лет) + 1000 (1 + 0,08Г)-10 = 80 х 6,7101 + 1000 х 0,4632.

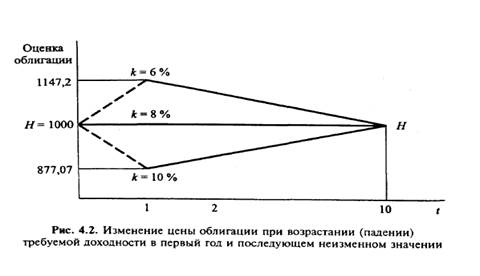
При возрастании требуемой доходности, например как в рассмотренном на рис. 4.2 случае, до 10% в течение первого года после выпуска облигации рыночная оценка облигации падает (P0 = 877,07 долл.), т.е. облигация продается u1089 с дисконтом. Дисконт равен разности номинала и цены — 123 долл. Рост k (например, из-за роста процентной ставки) означает, что если рассматривается инвестирование 1 тыс. долл., то в данный момент (при измененной процентной ставке) можно приобрести новую облигацию с аналогичным риском, по которой ежегодные выплаты составят 100 долл. (купонная ставка будет равна требуемой доходности). Так как для инвестора при сохранении уровня риска ежегодное получение 100 долл. предпочтительнее, чем 80 долл., то цена на облигацию с 8%-м купонным доходом будет падать. При неизменности процентной ставки в последующие годы до погашения цена будет расти с 877,1 долл. до 1000 долл. на момент погашения. Например, на конец первого года цена составит Р1 = С х РV анн (10%, 9 лет) + H(1,1)-9 = 884,8 долл., т.е. возрастет на 7,7 долл. Это составит для инвестора прирост капитала за год. Доходность прироста капитала равна 7,7 / 877,1 = 0,88%, текущая доходность равна 80 / 877,1 = 9,12%, общая доходность (ожидаемая) равна требуемой рыночной доходности 10%.

При падении требуемой доходности (из-за снижения риска эмитента или падения процентной ставки) цена облигации поднимется выше номинала и облигация будет продаваться с премией (например, при повышении 1с в первый год до 6 % цена достигнет 1147,2 долл.);

4) доходность к погашению, рассчитанную по правилу сложного процента, (yield to maturity —YТM). Это ставка дисконтирования, которая уравнивает РV всех будущих выплат с текущей ценой облигации. Для облигации со сроком обращения один год доходность к погашению аналогична общей доходности за год (ТY). Для среднесрочных и долгосрочных облигаций доходность к погашению можно рассматривать как ежегодную доходность, которую инвестор получит, если будет держать облигацию до погашения. На фиксированный момент времени YTM отражает сложившуюся на рынке требуемую доходность по данной облигации.

Доходность к погашению k находится путем решения уравнения степени п из данных значений номинала H, купонной выплаты С, срока погашения п и текущей цены Р:

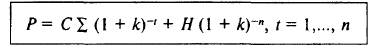
Решение осуществляется методом итераций, например по функции ВНДОХ Microsoft Exel (внутренняя норма доходности), которая требует задания следующих данных: текущая цена, денежные потоки. Так, для 3-летней облигации с одноразовыми выплатами в конце года в размере С, номиналом Я и текущей ценой Рввод данных выглядит следующим образом:

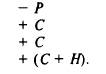
Приближенная оценка доходности к погашению (YTM) может быть получена из соотношений "цена — номинал" и текущей доходности.

Предложены различные формулы приближенной оценки доходности к погашению, например традиционная формула

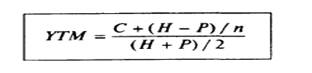
В ряде случаев лучшее приближенное значение дает формула

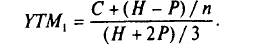
Например, при оценке доходности к погашению облигации с 5-летним сроком обращения и 10%-й купонной ставкой при номинале 1 тыс. долл., при текущей цене 1059,12 долл. точное значение, полученное из решения уравнения, составит 8,5 %, традиционная формула дает значение 8,56%, а YTM1 - 8,48%. Эта формула дает хорошее приближение при условиях: невысокое значение купонной ставки (ниже 50% годовых), близкие значения цены и номинала (если цена отличается от номинала более чем в 2 раза, то применение приближенных оценок недопустимо).

?Может ли значение доходности к погашению быть отрицательной величиной?

Бессрочные облигации— облигации без фиксированного срока погашения. Например, в Великобритании Undated gilts (термин gilts применяется для долгосрочных и среднесрочных государственных облигаций) представлены: 2,5%-ми консолями 1888 г.; 3,5%-ми военными облигациями, погашаемыми после 1952 г.; 4%-миконсолями. Под погашением понимается право правительства погасить облигацию, но так как рыночный курс ниже номинала, то нет смысла производить погашение.

Текущая цена бессрочной облигации определяется из отношения ежегодного дохода к рыночной ставке процента (требуемой доходности по облигационному выпуску):

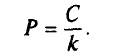
Данная формула получена из общей формулы оценки актива: Р = всех поступлений от актива. В данном случае поступления предполагаются на неограниченном временном промежутке:

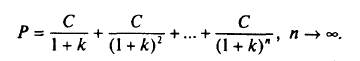
Умножив обе части уравнения на (1+k) и вычтя одно уравнение из другого, получим

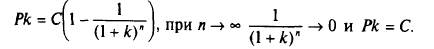
Индексируемые облигации.Для долгосрочных облигаций большое значение имеет инфляционный фактор. Защитой от возможной инфляции для инвестора будет приобретение индексируемой облигации, купонная ставка по которой меняется с изменением индекса розничных потребительских цен. Например, в Великобритании выпущенные в 1980-х гг. индексируемые облигации ориентировались на изменение цен корзины из 600 товаров:

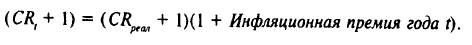
Первый выпуск индексируемых облигаций в Великобритании относится к 1981 г. (погашение — 1996 г.) с реальной купонной ставкой 2%. В те годы, когда инфляция достигала 8% годовых, номинальная купонная ставка составляла 10,16%, что гарантировало инвесторам защиту от инфляционного обесценивания капитала и колебаний процентных ставок. По последним выпускам индексируемых облигаций Великобритании реальная купонная ставка увеличена, но не превышает 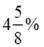годовых.

Важные соотношения для оценки облигаций

Рыночная цена облигации является индикатором изменения требуемой доходности на рынке по данному выпуску (данному эмитенту). Требуемая доходность для компании выступает как стоимость данного элемента капитала при отсутствии льгот по налогообложению при привлечении заемных средств. Когда купонная ставка процента СR равна доходности к погашению YTM (рассчитанной по правилу сложного процента), то облигация на моменты купонных выплат продается по номиналу. Исходя из этого соотношения эмитент устанавливает купонную ставку при принятии решения о размещении облигационного займа. Облигация с премией (текущая цена превышает номинал) означает, что доходность к погашению ниже купонной ставки. Если доходность к погашению больше купонной ставки, то цена облигации ниже номинала (табл. 4.1).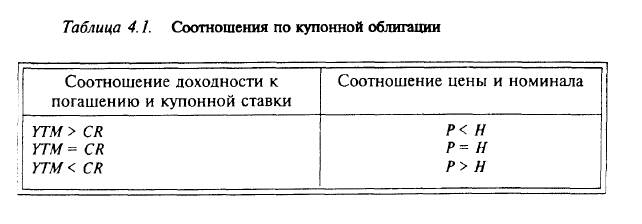

Эти соотношения работают "в обе стороны" и не требуют знания срока обращения облигации. Например, если купонная ставка по облигации равна 12%, а доходность к погашению 14%, то из соотношений табл. 4.1 видно, что облигация продается с дисконтом.

Лучшую информацию обеспечивают соотношения по текущей доходности (табл. 4.2).

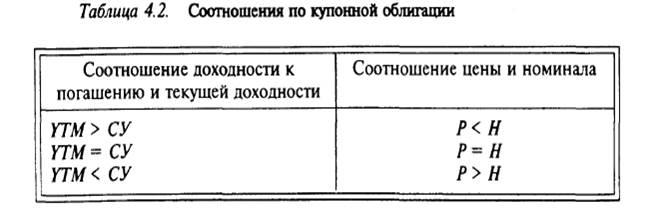
Например, облигация с номиналом 1 тыс. долл. и купонной ставкой 12% продается в настоящее время за 900 долл. Из соотношений табл. 4.1 видно, что доходность к погашению должна быть больше чем 12%. Из табл. 4.2 следует более точная оценка приближения: YTM > CY, CY = 120 / 900 = = 13,33%.