Анализ полученного оптимального решения

Итак, получен результат: определены значения объёмов производства для каждого вида продукции и соответствующее значение целевой функции, выражающее получаемую при этом прибыль.

Очень часто получения оптимального решения задачи оказывается недостаточно. Во многих случаях пользователю желательно исследовать полученное решение, чтобы ответить на целый ряд вопросов, возникающих при анализе результатов. Так, например, его может интересовать, насколько чувствительным является полученное оптимальное решение к изменению различных параметров исходной модели. Этому в известной мере могут помочь предлагаемые пользователю в окне Результаты поиска решения отчёты, составленные на основе полученного решения. Таких отчетов три типа: Результаты, Устойчивость и Пределы (см. Рис. 1.4.10).

2.2.1. Если в окне Результаты поиска решения выбрать первый тип отчёта - Результаты и нажать ОК, то на экране появится Отчет по результатам решения задачи, включающий в себя три таблицы (Рис. 2.3.1.1 и Рис.2.3.1.2).

Одновременно, внизу окна рабочей книги, где находятся ярлычки рабочих листов (Лист 1, Лист 2 и т.д.) появится ярлычок этого отчёта.

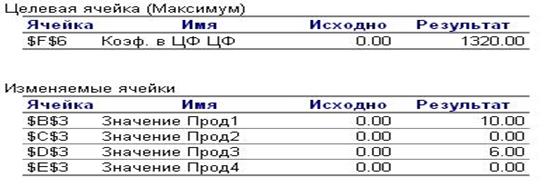
Рис. 2.2.1.1. Первые две таблицы отчёта по результатам

В первой таблице (Рис.2.2.1.1) приведено исходное (до начала вычислений) и окончательное (оптимальное) значение ячейки, в которой записана целевая функция задачи.

Во второй таблице (Рис.2.2.1.1) представлены значения искомых оптимизируемых переменных, исходные и полученные в результате решения задачи.

Последняя таблица (Рис.2.2.1.2) содержит результаты оптимального решения для ограничений и граничных условий.

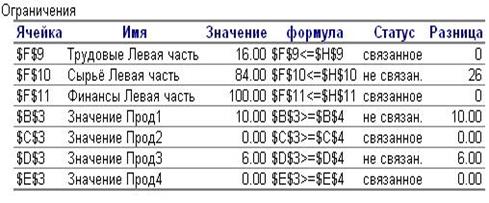
Рис. 2.2.1.2. Третья таблица отчёта по результатам

В графе Значение приведены рассчитанные оптимальные значения потребных ресурсов и оптимизируемых переменных.

В графе Формула приведены зависимости, которые были введены в диалоговое окно Поиск решения.

Графа Статус определяет связанными или несвязанными являются те или иные ограничения. Под «связанными» здесь понимаются ограничения, которые реализуются в оптимальном решении в виде жестких равенств. Так ресурсы Трудовые и Финансы в оптимальном решении используется до конца (без остатка) и поэтому является связанными, т.е. дефицитным. Последняя графа Разница определяет неиспользуемый остаток несвязанного ресурса, т.е. разность между потребным количеством ресурсов и их наличием (110-84=26 для ресурса Сырьё).

Для ограничений по объёму выпуска в этой графе указывается разность между значением выпуска данного вида продукции в полученным оптимальным решении и граничными условиями Так, как в нашем примере для всех видов продукции указана только нижняя граница равная 0, то в этой графе также приведены найденные оптимальные значения.

Хотя отчет по результатам не дает пользователю какой-либо дополнительной информации, которую он не мог бы получить из оптимального решения (см. Рис. 1.4.10), удобный формат отчёта позволяет быстро и легко оценить полученный результат.

2.2.2. Второй тип отчёта - Отчет по устойчивости – создается так же, как и предыдущий. Для данной задачи этот отчет, состоящий из двух таблиц, приведен на рис. 2.2.2.

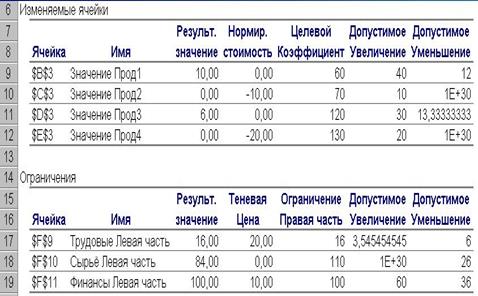
Рис. 2.2.2. Отчет по устойчивости

Отчет содержит информацию об изменяемых (оптимизируемых) переменных и ограничениях нашей модели. Он позволяет оценить, насколько чувствительным является полученное оптимальное решение к возможным изменениям параметров модели.

Первая часть отчета содержит информацию об изменяемых ячейках, содержащих значения объемов производства продукции. В графе "Результирующее значение" указываются найденные оптимальные значения оптимизируемых переменных.

В графе "Нормированная стоимость" (в некоторых версиях Excel эта графа называется "Редуцированная стоимость") приведены дополнительные двойственные переменные v_j (см. систему (2.3.4)) для каждого вида продукции. Величина этого показателя определяется как разность между единичной прибылью от производства единицы продукции данного вида и оценкой снижения общей прибыли за счет отвлечения ресурсов для производства данного вида продукции, взятой по теневым ценам этих ресурсов. Так, значения редуцированной стоимости для каждого вида продукции определяются следующим образом:

Вид Продукции	Целев. коэфф.	Теневая цена труд. рес.	Норма расхода труд.рес.	Теневая цена сырья	Норма расхода сырья	Теневая цена финанс.	Норма расхода финанс.	Нормир. стоимость
Прод.1	60 -	( 20 *	1 +	0 *	6 +	10 *	4 ) =
Прод.2	70 -	( 20 *	1 +	0 *	5 +	10 *	6 ) =	-10
Прод.3	120 -	( 20 *	1 +	0 *	4 +	10 *	10 ) =
Прод.4	130 -	( 20 *	1 +	0 *	3 +	10 *	13 ) =	-20

Если основные переменные вошли в оптимальное решение (в нашем примере х₁=10 и х₃=6), то их нормированная стоимость - дополнительные двойственные переменные v₁ и v₃ равны нулю. Если основные переменные не вошли в оптимальное решение, т.е. равны нулю (в примере х₂=0 и х₄=0), то соответствующие им дополнительные переменные v₂=-10 и v₄=-20 показывают, насколько уменьшится целевая функция при принудительном выпуске единицы данной продукции. Следовательно, если мы захотим принудительно выпустить единицу продукции Прод2, то целевая функция уменьшится на 10 единиц и будет равна 1320-10 1= 1310.

В следующей графе приведены коэффициенты целевой функции c_j. Напомним, что c_j– прибыль, получаемая в результате реализации единицы продукции j–го типа.

В последних двух графах первой таблицы даны Допустимое увеличение maxrс_j и Допустимое уменьшение minrс_j коэффициентов c_j целевой функции, при которых сохраняется структура оптимального плана, т.е. будет выгодно выпускать данную продукцию.

Так, для нашего случая для продукции П1 коэффициент оптимизируемой переменной с₁=60, может быть увеличен на величину maxrс₁=40 единиц (до значения, равного 60+40=100) или уменьшен на величину minrс₁=12 единиц (до значения 60-12=48) без изменения найденного решения (при сохранении без изменений всех остальных переменных). Таким образом, при изменении с₁ в пределах 48£с₁£100 будет по-прежнему выгодно выпускать продукцию П1. При этом значение целевой функции будет

F = 1320 + 10* rс₁

Аналогично определяются диапазоны возможного изменения коэффициентов целевой функции при остальных переменных.

Втораячасть отчета по устойчивости содержит информацию по ограничениям, накладываемым на оптимизируемые переменные. Первый столбец содержит данные о потребностях в ресурсах для оптимального решения. Во втором столбце указаны значения теневых цен на используемые виды ресурсов (мы поясним их содержание ниже). В третьем столбце мы видим имеющиеся ограничения на объем используемых ресурсов. Последние две колонки содержат данные о возможном увеличении или уменьшении объемов имеющихся ресурсов.

Как видно из отчета по результатам (Рис. 2.3.1), часть ограничений оказываются связанными. Для ограничений по ресурсам это происходит в том случае, если имеющийся объем ресурсов в процессе реализации оптимального решения используется полностью.

Для ограничений по оптимизируемым переменным это соответствует точному равенству оптимального объема выпуска значению верхней или нижней границы. Связанность ограничений заставляет нас отказаться от дальнейших поисков улучшений целевой функции. Однако на практике ограничения часто удается преодолевать. Поэтому после решения модели в некоторых случаях пользователю хотелось бы определить, как улучшится или ухудшится целевая функция в случае, если определенным образом удастся ослабить, то или иное ограничение.

Так, например, нужно определить, как увеличится прибыль, если бы имеющиеся объемы ресурсов могли быть увеличены. Столбец "Теневая цена" второй части отчета по устойчивости (Рис.2.3.2) содержит данные для ответа на этот вопрос.

Теневая цена ограничения выражает размер изменения целевой функции при увеличении имеющегося объема ресурсов данного вида на единицу (при условии, что все остальные переменные модели не изменятся).

Теневая цена связанных ресурсов положительна (в данном примере это трудовые и финансовые ресурсы) и единичное увеличение соответствующего объема ресурсов приведет к увеличению значения целевой функции -.

Так, например, из отчета по устойчивости (Рис.2.3.2) видно, что теневая цена трудового ресурса составляет 20 единиц. Следовательно, если увеличить имеющееся количество данного ресурса на некоторую величину, находящуюся в пределах от 0 и до 3.55 (допустимое увеличение), оптимальное значение целевой функции увеличится на 20 за каждую единицу увеличения имеющегося объема этого ресурса. Если же уменьшить имеющееся количество этого ресурса на некоторую величину, находящуюся в пределах от 0 до 6 (допустимое уменьшение), оптимальное значение целевой функции уменьшится на 20 за каждую единицу уменьшения имеющегося объема ресурса.

Допустим, что мы решили увеличить имеющийся объем ресурса на 3 единицы (16+3=19). Поскольку это увеличение находится в разрешенных пределах (допустимое увеличение составляет 3.55 единицу), мы вправе ожидать увеличения оптимального значения целевой функции на 20*3=60 единиц. Новое оптимальное значение целевой функции составит 1320+60=1380 (Рис. 3.2.3).

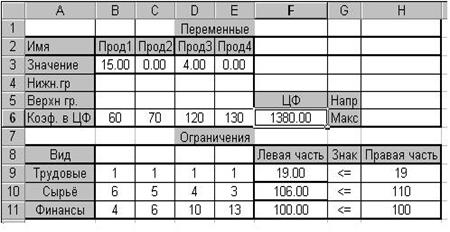
Рис. 2.2.3. Оптимальное решение при увеличении трудовых ресурсов

на 3 единицы.

Теперь рассмотрим теневые цены на несвязанные ограничения,покоторым ресурсы в оптимальном решении используются не полностью (недефицитные ресурсы). В нашем примере таким ресурсом является сырьё (см. Рис.2.2.1). Этот ресурс имеет теневую цену, равную 0, отсюда следует, что при увеличении имеющегося объема ресурса оптимальное значение целевой функции не изменится. Это и не удивительно, поскольку оптимальное решение оставляет 26 единицы этого ресурса неиспользованными. Однако, есть возможность сократить имеющийся объем этого ресурса на эту величину, не оказывая влияния на оптимальное решение.

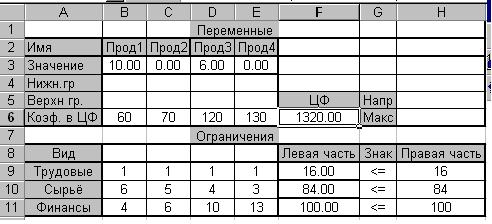
Рис. 2.2.4. Оптимальное решение при уменьшении

сырьевых ресурсов на 26 единицы.

Как мы видим на рис. 2.2.4, повторное решение задачи с новым значением ограничения по сырьевому ресурсу не только изменило оптимальное значение целевой функции,оно также определило новые значения оптимизируемых переменных, поскольку коррекция одного из ограничений изменила область существования решения.

Итак, в предыдущем примере, увеличив объем ресурса на 3 единицы, мы увеличили прибыль на 60 единиц. При этом правомерен вопрос: "Сколько мы можем платить за такое увеличение объема ресурса?" Ответ прост: "За каждую дополнительную единицу связанного (дефицитного) вида ресурсов мы можем платить надбавку, максимальная величина которой равна теневой цене 60/3=20". Даже заплатив такую максимальную надбавку (реально она должна быть меньше), мы получим ту же прибыль, что была до увеличения объема ресурсов.

Хотя теневые цены показывают, как изменится оптимальное значение целевой функции при изменении объемов имеющихся ресурсов, они не дают информации о том, как при этом изменятся значения оптимизируемых переменных. Чтобы определить новые значения оптимизируемых переменных, следует внести изменения в правые части ограничений и повторно решить модель.

Рассмотрим еще пример. Допустим, что мы решили выпустить на рынок новый вид продукции. Производство единицы такой продукции требует затрат 1 единицы трудовых ресурсов, 5 единицы сырьевых ресурсов, 8 единиц финансовых ресурсов и приносит150 единиц прибыли. Будет ли эта продукция прибыльной?

Ответ на этот вопрос можно дать на основе использования теневых цен. Прежде всего заметим, что производство новой продукции будет базироваться на тех же объемах ресурсов, что существовали до его начала. Таким образом, производство каждой единицы новой продукции отвлекает от прежнего производства вышеназванные ресурсы. Поскольку сырьевые ресурсы являются несвязанными, т. е. оптимальное решение использует их не полностью, отвлечение части этих ресурсов не вызовет изменения прибыли. Однако, отвлечение связанных (дефицитных) ресурса для производства единицы новой продукции вызовет снижение общей прибыли на величину 1*20+ 8*10=100 единиц. Это снижение, однако, будет компенсироваться повышением общей прибыли от производства единицы новой продукции, равным 120. Таким образом чистый эффект от производства единицы новой продукции составит 150-100=50, что говорит об эффективности выпуска новой продукции.

Итак, анализ отчета по устойчивости решения позволил выявить следующие взаимосвязи между теневыми ценами и нормированной стоимостью:

• теневые цены ресурсов определяют прирост (сокращение) общей прибыли при увеличении (уменьшении) на единицу имеющегося объема дефицитных ресурсов;

• недефицитные ресурсы имеют нулевую теневую цену;

• нормированная стоимость данной продукции равна разности между её единичной прибылью и суммой произведений ресурсных коэффициентов на теневые цены;

• виды продукции, имеющие отрицательную нормированную стоимость, являются неэффективными для производства.

Ранее при рассмотрении столбцов "Допустимое увеличение" и "Допустимое уменьшение" отчета по устойчивости мы определяли допустимые изменения коэффициентов целевой функции, которые возможны без изменения найденного оптимального решения при условии, что все остальные параметры модели останутся неизменными. Однако иногда может потребоваться определить возможности одновременного изменения коэффициентов целевой функции в рамках найденного решения. Выделяются следующие две ситуации.

1. Все переменные, по которым предполагается вносить изменения в показатели единичной прибыли, имеют ненулевые значения нормированной стоимости.

2. По меньшей мере одна переменная, в коэффициенты целевой функции которых предполагается вносить изменения, имеет нулевую нормированную стоимость.

Для первого случая существует следующее правило. Найденное решение сохранится, если изменения коэффициентов целевой функции будут произведены в пределах, заданных в столбцах "Допустимое увеличение" и "Допустимое уменьшение" отчета по устойчивости.

Для второго случая следует вычислить показатель r_j, по следующим формулам.

r_j = rC_j / I_j ; еслиrC_j >= 0

r_j = - rC_j / D_j ; еслиrC_j < 0

где C_j, - первоначальное значение коэффициента целевой функции для переменной П_j;

rC_j,- планируемое изменение C_j;

I_j - допустимое увеличение C_j в соответствии с отчетом по устойчивости;

D_j - допустимое уменьшение с, в соответствии с отчетом по устойчи­вости.

Заметим, что r_j измеряет отношение планируемых изменений величины C_j к максимально возможному изменению, при котором сохраняется данное оптимальное решение. Если изменяется только один из коэффициентов целевой функции, найденное оптимальное решение сохранится, при условии выполнения соотношения r_j<=1. Аналогично, если более чем один коэффициент целевой функции изменяется, найденное оптимальное решение сохранится при условии выполнения соотношения år_j<=1. (Заметим, что даже в случае невыполнения указанного соотношения оптимальное решение может сохраниться,хотя это не может гарантироваться.)

2.2.3. Последний из трех отчетов - Отчет по пределам для приведенного на Рис. 1.4.10 оптимального решения модели мы видим на Рис. 2.2.5.

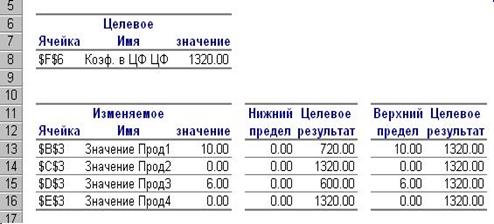
Рис. 2.2.5. Отчет по пределам.

Этот отчет содержит оптимальные значения целевой функции (прибыли) и независимых переменных (объемов производства). Кроме того, отчет по пределам дает возможностьувидеть, как изменится значение целевой функции, если независимые переменные будут принимать свои предельные (верхние или нижние) значения. Так, значения объемов производства в столбце "Нижний предел" показывают, какие минимальные значения эти переменные могут принимать, в то время как остальные независимые переменные остаются без изменений и выполняются все ограничения модели. Аналогично в столбце "Верхний предел" мы видим максимально возможные значения переменных при сохранении неизменности всех остальных переменных и соблюдении ограничений модели.

Параметрический анализ

2.3.1. Для задач распределения ресурсов наибольший интерес представляет решение двух задач вариантного анализа:

- параметрического анализа, в ходе которого решаются задачи при различных значениях одного из параметров;

- поиск решения по нескольким целевым функциям.

В данном разделе рассмотрим параметрический анализ задачи контрольного примера при различных значениях имеющихся финансов.

Составим таблицу рассматриваемых вариантов (Рис. 2.4.1).

Вариант
Финансы

Рис. 2.3.1.

2.3.2. Выведите на экран таблицу с полученным оптимальным решением (Рис. 1.4.10).

2.3.3. Удалите результат решения в В3:Е3:

- выделите блок ячеек В3:Е3;

- <Delete>.

2.3.4. В ячейку Н11 введите финансы варианта 1 - 50.

2.3.5. F6 - Сервис - Поиск решения - Выполнить. На экране результаты поиска решения контрольного примера для варианта финансы=50 и диалоговое окно Результаты поиска решения. (Рис. 2.3.2).

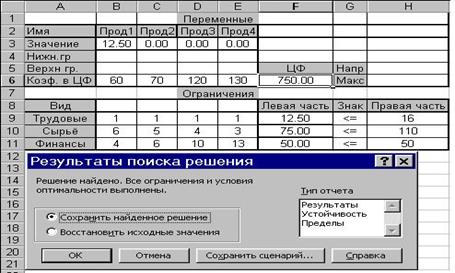
Рис. 2.3.2.

2.3.6. Посленажатия кнопки Сохранить сценарий и появления на экране диалогового окна Сохранение сценария -ввести имя сценария - Финансы=50 - ОК. (Рис. 2.3.3).

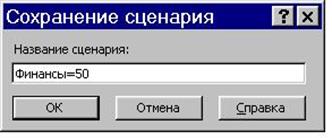
Рис. 2.3.3.

2.3.7. Аналогично пунктам 2.3.2 - 2.3.6 найти решения для всех последующих вариантов вводя соответствующие значения финансов и названия сценариев.

2.3.8. Представление результатов решения.

2.3.8.1. Сервис - Сценарии - на экране диалоговое окно Диспетчер сценариев (Рис. 2.4.4).

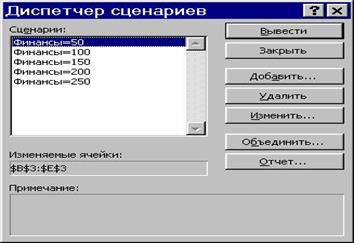
Рис. 2.3.4.

2.3.8.2. Выбрать Отчёт - на экране диалоговое окно Отчёт по сценариям (Рис. 2.3.5).

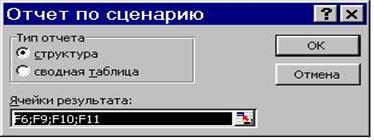
Рис. 2.3.5.

2.3.8.3. Структура - ОК - на экране отчёт Итоговый сценарий в котором приведены результаты решения контрольного примера для всех вариантов значений финансов (Рис. 2.3.6).

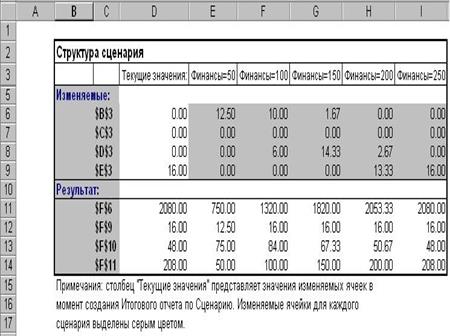
Рис. 2.3.5.

2.3.8.4. Для удобства дальнейшей работы выполним редактирование Итогового сценария:

- Удалите пустые столбцы А и В и столбец D Текущее значение;

- Выделите столбцы C - G (Финансы=50 - Финансы=250) и уменьшите их ширину - Формат - Столбец - Автоподбор ширины;

- Удалите строки 5 и 10;

- В ячейки А5:А8, где сейчас записаны адреса изменяемых ячеек $B$3 - $E$3, введите названия их содержимого - Прод1 - Прод4;

- В ячейку А9 (где сейчас $F$6) введите название Прибыль, а в ячейки А10:А12 названия видов ресурсов - Трудовые, Сырьё, Финансы;

- Увеличьте ширину столбца А - Формат - Столбец - Автоподбор ширины;

- Во вторую строку введите заголовок - Параметрический анализ оптимальных решений по финансам;

- Уберите примечание.

После этого Итоговый сценарий будет выглядеть так, как показано на рис. 2.3.7.

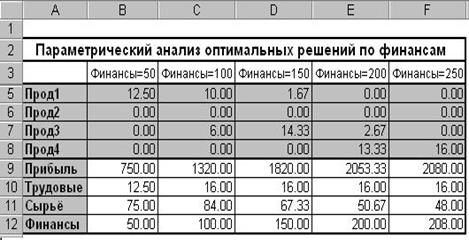
Рис. 2.3.7.

2.3.9. Для наглядности представления параметрического анализа на основании отредактированной таблицы Итогового сценария построим графики.