Переменная ставка процентов

Необходимо отметить, что основная формула сложных процентов предполагает постояннуюпроцентную ставку на протяжении всего срока начисления процентов. Однако, предоставляя долгосрочную ссуду, часто используют изменяющиеся во времени, но заранее зафиксированные для каждого периода ставки сложных процентов. В случае использования переменных процентных ставок, формула наращения имеет следующий вид:

FV = PV*(1+ r₁)ⁿ *( 1+ r₂)ⁿ *…(1+ r_k )ⁿ = 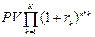( 1‑26)

гдеr_k – последовательные во времени значения процентных ставок;

n_k– длительность периодов, в течение которых используются соответствующие ставки.

Пример 1‑19

Фирма получила кредит в банке на сумму 250000долларов сроком на 5 лет. Процентная ставка по кредиту определена:

для первого года – в 10% для 1-го года,

для 2-го года предусмотрена надбавка к процентной ставке в размере 1,5%,

для последующих лет предусмотрена надбавка к процентной ставке второго года в размере 1%.

Определить сумму долга, подлежащую погашению в конце срока займа

Решение

FV = PV *(1 + r₁)ⁿ¹ * (1 + r₂)ⁿ² * … * (1 + r_k)^nk =

=250000 * (1 + 0,1) * (1 + 0,115) * (1 + 0,125)³ = 436581.3 доллара

Таким образом, сумма, подлежащая погашению в конце срока займа, составит 436581.3 доллара, из которых 250000 долларов являются непосредственно суммой долга, а 186581.3 доллара – проценты по долгу.

Определение срока ссуды и величины процентной ставки

Так же как для простых процентов, для сложных процентов необходимо иметь формулы, позволяющие определить недостающие параметры финансовой операции

ðсрок ссуды:

n = [ln (FV / PV)] / [ln (1 + r)] =

= [ln (FV / PV) ] / [ln(1 + r / m)*m] ( 1‑27)

ðставка сложных процентов:

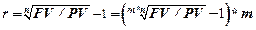( 1‑28)

Пример 1‑20

Рассчитать, через сколько лет вклад размером 1 млн. руб. достигнет 1 млрд., если годовая ставка процента по вкладу 16,79% и на­числение процентов производится ежеквартально.

Решение

n = ln (FV / PV) ] / [ln(1 + r / m)*m]

= (ln(1000000/1000)/(ln(1+r/4)*4) = 42.2 года

Пример 1‑21

Сумма 10000 руб. была положена на депозит на 2 года с полугодовым начислением процентов. По окончании была получена сумма 12000.

Определите величину банковского процента.

Решение.

=

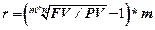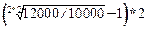= 9.32%

Пример 1‑22

В контракте предусматривается погашение обязательств через 120 дней в сумме 1200 долларов, при первоначальной сумме долга 1150 долларов. Определить доходность операции для кредитора в виде процентной ставки.

Решение

Рассчитываем годовую процентную ставку, используя формулу "обыкновенного процента", поскольку в условиях сделки нет ссылки на "точный процент":

r = [(FV - PV) /(PV * t)] * T =

= [(1200 - 1150) /(1150 * 120)] * 360 = 0,13

Таким образом, доходность финансовой операции составит 13% годовых, что соответствует весьма высокодоходной финансовой операции, т.к. обычно доходность подобных операций колеблется от 2% до 8%.