Абораторная работа №4. Влияние фактора неопределенности на экономические расчеты. Оптимальный портфель.

ариант 1

Вопрос 1. Снижение риска портфеля на основе диверсификации.

Вопрос 2.Методы снижения риска. Опционы.

Вопрос 3.Диверсификация. Достоинства и недостатки этого метода.

Вопрос 4.Статистически анализ финансового рынка. Однофакторная модель.

Задача 1. С помощью компьютера найден оптимальный портфель Марковица для трех ценных бумаг с эффективностями и рисками: (4,13); (15,40); (40,70); нижняя граница доходности задана равной 12. Доли бумаг оказались равными: 50%, 20% ,30%. Определите риск и доходность для данного портфеля.

Задача 2. Запишем вариацию доходности портфеля в форме: и назовем величину портфельной ковариацией доходности 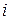-й ценной бумаги. Доказать, что в оптимальном портфеле эти ковариации пропорциональны превышению эффективности ценных бумаг над безрисковыми вложениями (подразумевается, что последние на рынке имеются).

Задача 3. Найдите детерминированный вариант процентной ставки, если ее начисление происходит дважды: первая половина в момент 0,8; вторая половина — в момент 1,1.

Задача 4. Начальный капитал «челнока» равен 170 000 рублей. Опытные люди сказали ему, что в результате по­ездки за товаром и его последующей реализации капитал может с равной вероятностью возрасти в два раза, не измениться или уменьшиться в три раза (с вычетом со­путствующих издержек). Найти среднюю ожидаемую до­ходность планируемой операции.

ариант 2

Вопрос 1. Снижение риска портфеля на основе диверсификации.

Вопрос 2. Статистически анализ финансового рынка. Многофакторная модель.

Вопрос 3. Снижение риска портфеля с помощью опционов на покупку.

Вопрос 4. Страхование. Достоинство и недостатки метода.

Задача 1. Найти детерминированный вариант процентной ставки, если с вероятностью 4/6 ее начисление происходит в момент 0,9, и с вероятностью 2/6— в момент 1,1.

Задача 2. С помощью компьютера найден оптимальный портфель Марковица для трех ценных бумаг с эффективностями и рисками: (4,10); (10,40); (40,80); нижняя граница доходности задана равной 15. Доли бумаг оказались равными: 60%, 10% ,30%. Определите риск и доходность для данного портфеля.

Задача 3. Запишем вариацию доходности портфеля в форме: и назовем величину портфельной ковариацией доходности 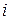-й ценной бумаги. Доказать, что в оптимальном портфеле эти ковариации пропорциональны превышению эффективности ценных бумаг над безрисковыми вложениями (подразумевается, что последние на рынке имеются).

Задача 4. Запас золота в месторождении известен, как и начальные инвестиции в его разработку. Фактиче­ски полная отдача месторождения тоже фиксирована, следовательно, доходность (в процентах годовых) будет
зависеть от длительности выработки месторождения: чем дольше будет вырабатываться месторождение, тем больше доходность.

ариант 3

Вопрос 1.От каких факторов зависит эффективность рискованных ценных бумаг?

Вопрос 2. Кредитный риск и способы его уменьшения.

Вопрос 3. Что означает отрицательная (положительная) корреляционная связь.

Вопрос 4. Какой портфель называют безрисковым?

Задача 1. По договору в течение 6 лет в конце каждого квартала издательство переводит на счет автора случайную сумму денег (зависит от числа проданных книг). Предположим, что эта сумма равномерно распределена от 21 000 до 24 000 руб. Как найти современную величину этой ренты?

Задача 2. Найти детерминированный вариант процентной ставки, если с вероятностью 1/5 ее начисление происходит в момент 0,9, и с вероятностью 4/5 — в момент 1,3

Задача 3. С помощью компьютера найден оптимальный портфель максимальной эффективности для трех ценных бумаг с доходностью и риском: (4,10); (10,40); (40,80); верхняя граница риска задана равной 50. Доли бумаг оказались равными: 6%, 34% ,60%. Определите риск и доходность для данного портфеля.

Задача 4. Пусть операции и некоррелированы, найдем риск операции (например, денег не хватит на проведение обеих операций в полном объеме):

	-5
0,2	0,8	0,7	0,3

Рассчитайте риск операции

ариант 4

Вопрос 1. Что характеризует ковариация двух видов ценных бумаг?

Вопрос 2. Страхование. Достоинство и недостатки метода.

Вопрос 3. Основные предположения, принимаемые при построении модели оптимизации портфеля.

Вопрос 4. Кредитный риск и методы его уменьшения.

Задача 1. Сегодня днем цена акции равна 140 руб. За сутки цена может вырасти на 20% с вероятностью 1/3, с такой же вероятностью уменьшится в 1,1 раза и с такой же вероятностью 1/3 остаться равной 140 руб. Найдите распределение цены акции завтра и послезавтра.

Задача 2. С помощью компьютера найден оптимальный портфель Марковица для трех ценных бумаг с эффективностями и рисками: (4,10); (10,40); (40,80); нижняя граница доходности задана равной 17. Доли бумаг оказались равными: 46%, 20% ,34%. Определите минимальный риск для данного портфеля.

Задача 3. Начальный капитал «челнока» равен 170 000 рублей. Опытные люди сказали ему, что в результате поездки за товаром и его последующей реализации капитал может с равной вероятностью возрасти в три раза, не измениться или уменьшиться в два раза (с вычетом со­путствующих издержек). Найти среднюю ожидаемую до­ходность планируемой операции.

Задача 4. Найти детерминированный вариант процентной ставки, если с вероятностью 3/5 ее начисление происходит в момент 0,9, и с вероятностью 2/5 — в момент 1,3

ариант 5

Вопрос 1. Оптимизация портфеля при возможности безрисковых вложений

Вопрос 2. Диверсификация. Достоинства и недостатки этого метода.

Вопрос 3. Форвардная торговля. Примеры.

Вопрос 4. Финансовые фьючерсы. Примеры.

Задача 1. С помощью компьютера найден оптимальный портфель Марковица для трех ценных бумаг с эффективностями и рисками: (4,10); (10,40); (40,80); нижняя граница доходности задана равной 15. Доли бумаг оказались равными: 6%, 62% ,32%. Определите ожидаемую доходность для данного портфеля.

Задача 2. Статистика запросов кредитов в банке такова: 30% — государственные органы, 40% — другие банки и 50% — физические лица. Вероятности невозврата взятого кредита соответственно таковы: 0,01; 0,05 и 0,2. Найти вероятность невозврата очередного запроса на кредит.(ответ округлить до тысячных)

Задача 3. Запишем вариацию доходности портфеля в форме: и назовем величину портфельной ковариацией доходности 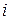-й ценной бумаги. Доказать, что в оптимальном портфеле эти ковариации пропорциональны превышению эффективности ценных бумаг над безрисковыми вложениями (подразумевается, что последние на рынке имеются).

Задача 4. Осуществляется одновременно множество инвестиционных проектов. Инвестиции в каждый проект равны 1 500 000, а будущий годовой доход случаен по проектам — равномерно распределен от 50 000 до 170 000 руб. Какая часть проектов окупится в течение 7 лет? (Процентная ставка 11% в год)

ариант 6

Вопрос 1. Страхование. Достоинство и недостатки метода.

Вопрос 2. Основные предположения, принимаемые при построении модели оптимизации портфеля.

Вопрос 3. Чем отличается форвардный контракт от фьючерсного контракта?

Вопрос 4. Финансовый риск в деятельности страховой компании.

Задача 1. Начальный капитал «челнока» равен 220 000 рублей. Опытные люди сказали ему, что в результате поездки за товаром и его последующей реализации капитал может с равной вероятностью возрасти в пять раз, не измениться или уменьшиться в два раза (с вычетом со­путствующих издержек). Найти среднюю ожидаемую до­ходность планируемой операции.

Задача 2. Рассчитайте среднюю ожидаемую доходность и среднеквадратическое отклонение операции Q, если

	0,2	0,18	0,32	0,1	0,2

Задача 3. В начале года страховая компания кладет в банк 100 000 д.е. под 12 % годовых. В любой момент года возможен страховой случай, когда компании придется выплатить 100 000 д.е. страхового возмещения. Найдите математическое ожидание суммы на счете компании к концу года.

Задача 4. С помощью компьютера найден оптимальный портфель Марковица для трех ценных бумаг с эффективностями и рисками: (6,10); (30,40); (30,80); нижняя граница доходности задана равной 19. Доли бумаг оказались равными: 40%, 40% ,20%. Определите риск и доходность для данного портфеля.

ариант 7

Вопрос 1. Оценка вклада ценной бумаги в общую ожидаемую эффективность портфеля.

Вопрос 2. Финансовые фьючерсы. Примеры.

Вопрос 3. Финансовый риск в деятельности страховой компании.

Вопрос 4. Модель CAMP.

Задача 1. Проанализируйте инвестиционный проект, начальные инвестиции в который равны 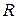в момент 0, а поток будущих доходов есть пуассоновский поток 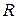платежей с плотностью платеж в ед. времени. Ставка процента равна .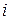

Задача 2. Пусть операции и некоррелированы, найдем риск операции (например, денег не хватит на проведение обеих операций в полном объеме):

	-5
0,2	0,8	0,7	0,3

Рассчитайте риск операции .

Задача 3. Сегодня днем цена акции равна 520 руб. За сутки цена может вырасти на 27% с вероятностью 1/6, с вероятностью 2/6 уменьшится в 1,9 раза и с вероятностью 3/6 остаться равной 520 руб. Найдите распределение цены акции завтра и послезавтра.

Задача 4. С помощью компьютера найден оптимальный портфель Марковица для трех ценных бумаг с эффективностями и рисками: (40,50); (10,20); (100,90); нижняя граница доходности задана равной 14. Доли бумаг оказались равными: 46%, 28% ,26%. Определите риск и доходность для данного портфеля.

ариант 8

Вопрос 1. Кредитный риск и методы его уменьшения.

Вопрос 2. Статистически анализ финансового рынка. Многофакторная модель.

Вопрос 3. Плавающая ставка процента.

Вопрос 4. Случайные потоки платежей.

Задача 1. По договору в течение 7 лет в конце каждого квартала издательство переводит на счет автора случайную сумму денег (зависит от числа проданных книг). Предположим, что эта сумма равномерно распределена от 15 000 до 34 000 руб. Как найти современную величину этой ренты?

Задача 2. Начальный капитал «челнока» равен 220 000 рублей. Опытные люди сказали ему, что в результате поездки за товаром и его последующей реализации капитал может с равной вероятностью возрасти в три раза, не измениться или уменьшиться в два раза (с вычетом со­путствующих издержек). Найти среднюю ожидаемую до­ходность планируемой операции.

Задача 3. Запишем вариацию доходности портфеля в форме: и назовем величину портфельной ковариацией доходности 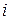-й ценной бумаги. Доказать, что в оптимальном портфеле эти ковариации пропорциональны превышению эффективности ценных бумаг над безрисковыми вложениями (подразумевается, что последние на рынке имеются).

Задача 4. Рассчитайте среднюю ожидаемую доходность и среднеквадратическое отклонение операции Q, если

						-70
	0,25	0,18	0,12	0,05	0,03	0,02	0,2	0,15

ариант 9

Вопрос 1. Общее понятие детерминированного эквивалента финансового показателя

Вопрос 2. Статистически анализ финансового рынка. Многофакторная модель.

Вопрос 3. Плавающая ставка процента.

Вопрос 4. Хеджирование, приведите примеры.

Задача 1. Запишем вариацию доходности портфеля в форме: и назовем величину портфельной ковариацией доходности 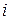-й ценной бумаги. Доказать, что в оптимальном портфеле эти ковариации пропорциональны превышению эффективности ценных бумаг над безрисковыми вложениями (подразумевается, что последние на рынке имеются).

Задача 2. Найдите математическое ожидание современной величины случайной ренты: платежи R осуществляются раз в год с равной вероятностью либо 1 октября, либо 1 декабря. Ставка равна i

Задача 3. С помощью компьютера найден оптимальный портфель Марковица для трех ценных бумаг с эффективностями и рисками: (4,10); (10,40); (40,80); нижняя граница доходности задана равной 15. Доли бумаг оказались равными: 46%, 28% ,26%. Определите риск и доходность для данного портфеля.

Задача 4. По договору в течение 3 лет в конце каждого квартала издательство переводит на счет автора случайную сумму денег (зависит от числа проданных книг). Предположим, что эта сумма равномерно распределена от 30 000 до 65 000 руб. Как найти современную величину этой ренты?

ариант 10

Вопрос 1. Диверсификация. Достоинства и недостатки этого метода.

Вопрос 2. Чем отличается форвардный контракт от фьючерсного контракта?

Вопрос 3. Рисковые инвестиционные процессы

Вопрос 4. Подсчет доходности вероятностных операций в условиях неопределенности.

Задача 1. Рассчитайте среднюю ожидаемую доходность и среднеквадратическое отклонение операции Q, если

	0,2	0,18	0,32	0,1	0,2

Задача 2. Найти детерминированный вариант процентной ставки, если с вероятностью 4/5 ее начисление происходит в момент 0,9, и с вероятностью 1/5 — в момент 1,3

Задача 3. Статистика запросов кредитов в банке такова: 10% — государственные органы, 20% — другие банки и 70% — физические лица. Вероятности невозврата взятого кредита соответственно таковы: 0,01; 0,05 и 0,32. Найти вероятность невозврата очередного запроса на кредит.(ответ округлить до тысячных)

Задача 4. С помощью компьютера найден оптимальный портфель Марковица для трех ценных бумаг с эффективностями и рисками: (42,10); (10,30); (40,50); нижняя граница доходности задана равной 10. Доли бумаг оказались равными: 16%, 52% ,32%. Определите ожидаемую доходность для данного портфеля.

ариант 11

Вопрос 1. Статистически анализ финансового рынка. Многофакторная модель.

Вопрос 2. Финансовые фьючерсы. Примеры.

Вопрос 3. Оценка вклада ценной бумаги в общую ожидаемую эффективность портфеля.

Вопрос 4. Случайные потоки платежей.

Задача 1. Начальный капитал «челнока» равен 50 000 рублей. Опытные люди сказали ему, что в результате поездки за товаром и его последующей реализации капитал может с равной вероятностью возрасти в семь раз, не измениться или уменьшиться в два раза (с вычетом со­путствующих издержек). Найти среднюю ожидаемую доходность планируемой операции.

Задача 2. Найдите математическое ожидание современной величины случайной ренты: платежи R осуществляются раз в год с равной вероятностью либо 1 сентября, либо 1 декабря. Ставка равна i

Задача 3. По договору в течение 5 лет в конце каждого квартала издательство переводит на счет автора случайную сумму денег (зависит от числа проданных книг). Предположим, что эта сумма равномерно распределена от 75 000 до 150 000 руб. Как найти современную величину этой ренты?

Задача 4. Осуществляется одновременно множество инвестиционных проектов. Инвестиции в каждый проект равны 150 000, а будущий годовой доход случаен по проектам — равномерно распределен от 70 000 до 90 000 руб. Какая часть проектов окупится в течение 4 лет? (Процентная ставка 11.5% в год)

ариант 12

Вопрос 1. Модель CAMP.

Вопрос 2. Методы снижения риска. Опционы.

Вопрос 3. Диверсификация. Достоинства и недостатки этого метода.

Вопрос 4. Финансовые фьючерсы. Примеры.

Задача 1. С помощью компьютера найден оптимальный портфель Марковица для трех ценных бумаг с эффективностями и рисками: (9,9); (10,20); (40,80); нижняя граница доходности задана равной 13. Доли бумаг оказались равными: 46%, 20%,34%. Определите минимальный риск для данного портфеля.

Задача 2. Запишем вариацию доходности портфеля в форме: и назовем величину портфельной ковариацией доходности 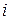-й ценной бумаги. Доказать, что в оптимальном портфеле эти ковариации пропорциональны превышению эффективности ценных бумаг над безрисковыми вложениями (подразумевается, что последние на рынке имеются).

Задача 3. Осуществляется одновременно множество инвестиционных проектов. Инвестиции в каждый проект равны 250 000, а будущий годовой доход случаен по проектам — равномерно распределен от 30 000 до 80 000 руб. Какая часть проектов окупится в течение 5 лет? (Процентная ставка 9% в год)

Задача 4. Рассчитайте среднюю ожидаемую доходность и среднеквадратическое отклонение операции Q, если

	0,5	0,18	0,12	0,1	0,1

ариант 13

Вопрос 1. Что характеризует ковариация двух видов ценных бумаг?

Вопрос 2. Основные предположения, принимаемые при построении модели оптимизации портфеля.

Вопрос 3. Чем отличается форвардный контракт от фьючерсного контракта?

Вопрос 4. Основной принцип хеджирования. Примеры.

Задача 1. Запишем вариацию доходности портфеля в форме: и назовем величину портфельной ковариацией доходности 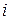-й ценной бумаги. Доказать, что в оптимальном портфеле эти ковариации пропорциональны превышению эффективности ценных бумаг над безрисковыми вложениями (подразумевается, что последние на рынке имеются).

Задача 2. Найдите детерминированный вариант процентной ставки, если момент ее начисления равномерно, распределен на временном отрезке [0,1; 1,1].

Задача 3. Сегодня днем цена акции равна 520 руб. За сутки цена может вырасти на 17% с вероятностью 1/2, с вероятностью1/3 уменьшится в 1,9 раза и с вероятностью 1/6 остаться равной 520 руб. Найдите распределение цены акции завтра и послезавтра.

Задача 4. С помощью компьютера найден оптимальный портфель Марковица для трех ценных бумаг с эффективностями и рисками: (4,10); (10,40); (40,80); нижняя граница доходности задана равной 15. Доли бумаг оказались равными: 46%, 20% ,34%. Определите минимальный риск для данного портфеля.

ариант 14

Вопрос 1. Диверсификация. Достоинства и недостатки этого метода.

Вопрос 2. Рисковые инвестиционные процессы

Вопрос 3. Подсчет доходности вероятностных операций в условиях неопределенности.

Вопрос 4. Общее понятие детерминированного эквивалента финансового показателя.

Задача 1. По договору в течение 9 лет в конце каждого квартала издательство переводит на счет автора случайную сумму денег (зависит от числа проданных книг). Предположим, что эта сумма равномерно распределена от 30 000 до 190 000 руб. Как найти современную величину этой ренты?

Задача 2. Найдите математическое ожидание современной величины случайной ренты: платежи R осуществляются раз в год с равной вероятностью либо 1 октября, либо 1 ноября. Ставка равна i

Задача 3. Запишем вариацию доходности портфеля в форме: и назовем величину портфельной ковариацией доходности 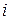-й ценной бумаги. Доказать, что в оптимальном портфеле эти ковариации пропорциональны превышению эффективности ценных бумаг над безрисковыми вложениями (подразумевается, что последние на рынке имеются).

Задача 4. Найдите математическое ожидание современной величины случайной ренты: платежи R осуществляются раз в год с равной вероятностью либо 1 октября, либо 1 декабря. Ставка равна i

ариант 15

Вопрос 1. Методы снижения риска. Опционы.

Вопрос 2. Форвардная торговля. Примеры.

Вопрос 3. Оценка вклада ценной бумаги в общую ожидаемую эффективность портфеля.

Вопрос 4. Случайные потоки платежей.

Задача 1. С помощью компьютера найден оптимальный портфель Марковица для трех ценных бумаг с эффективностями и рисками: (7,10); (15,40); (45,80); нижняя граница доходности задана равной 16. Доли бумаг оказались равными: 46%, 20% ,34%. Определите минимальный риск для данного портфеля.

Задача 2. Пусть операции и некоррелированы, найдем риск операции (например, денег не хватит на проведение обеих операций в полном объеме):

	-90
0,25	0,75	0,45	0,55

Рассчитайте риск операции .

Задача 3. Запас золота в месторождении известен, как и начальные инвестиции в его разработку. Фактиче­ски полная отдача месторождения тоже фиксирована, следовательно, доходность (в процентах годовых) будет
зависеть от длительности выработки месторождения: чем дольше будет вырабатываться месторождение, тем больше доходность.

Задача 4. Найдите математическое ожидание современной величины случайной ренты: платежи R осуществляются раз в год с равной вероятностью либо 15 сентября, либо 1 ноября. Ставка равна i

ариант 16

Вопрос 1. Страхование. Достоинство и недостатки метода.

Вопрос 2. Финансовые фьючерсы. Примеры.

Вопрос 3. Финансовый риск в деятельности страховой компании.

Вопрос 4. Подсчет доходности вероятностных операций в условиях неопределенности.

Задача 1. Начальный капитал «челнока» равен 220 000 рублей. Опытные люди сказали ему, что в результате поездки за товаром и его последующей реализации капитал может с равной вероятностью возрасти в три раза, не измениться или уменьшиться в два раза (с вычетом со­путствующих издержек). Найти среднюю ожидаемую до­ходность планируемой операции.

Задача 2. В начале года страховая компания кладет в банк 100 000 д.е. под 12 % годовых. В любой момент года возможен страховой случай, когда компании придется выплатить 100 000 д.е. страхового возмещения. Найдите математическое ожидание суммы на счете компании к концу года.

Задача 3. Сегодня днем цена акции равна 1220 руб. За сутки цена может вырасти на 17% с вероятностью 1/7, с вероятностью 4/7 уменьшится в 1,9 раза и с вероятностью 2/7 остаться равной 1220 руб. Найдите распределение цены акции завтра и послезавтра.

Задача 4. Рассчитайте среднюю ожидаемую доходность и среднеквадратическое отклонение операции Q, если

	0,2	0,18	0,32	0,1	0,2

ариант 17

Вопрос 1. Статистически анализ финансового рынка. Многофакторная модель.

Вопрос 2. Чем отличается форвардный контракт от фьючерсного контракта?

Вопрос 3. Модель CAMP

Вопрос 4. Общее понятие детерминированного эквивалента финансового показателя.

Задача 1. Пусть операции и некоррелированы, найдем риск операции (например, денег не хватит на проведение обеих операций в полном объеме):

	-50
0,3	0,7	0,7	0,3

Рассчитайте риск операции .

Задача 2. Найдите математическое ожидание современной величины случайной ренты: платежи R осуществляются раз в год с равной вероятностью либо 1 сентября, либо 1 ноября. Ставка равна i

Задача 3. Запишем вариацию доходности портфеля в форме: и назовем величину портфельной ковариацией доходности 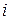-й ценной бумаги. Доказать, что в оптимальном портфеле эти ковариации пропорциональны превышению эффективности ценных бумаг над безрисковыми вложениями (подразумевается, что последние на рынке имеются).

Задача 4. С помощью компьютера найден оптимальный портфель Марковица для трех ценных бумаг с эффективностями и рисками: (14,10); (20,40); (57,80); нижняя граница доходности задана равной 25. Доли бумаг оказались равными: 46%, 10% ,24%. Определите минимальный риск для данного портфеля.

ариант 18

Вопрос 1. Оптимизация портфеля при возможности безрисковых вложений

Вопрос 2. Финансовые фьючерсы. Примеры.

Вопрос 3. Основной принцип хеджирования. Примеры.

Вопрос 4. Рисковые инвестиционные процессы

Задача 1. По договору в течение 10 лет в конце каждого квартала издательство переводит на счет автора случайную сумму денег (зависит от числа проданных книг). Предположим, что эта сумма равномерно распределена от 10 000 до 50 000 руб. Как найти современную величину этой ренты?

Задача 2. Запишем вариацию доходности портфеля в форме: и назовем величину портфельной ковариацией доходности 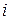-й ценной бумаги. Доказать, что в оптимальном портфеле эти ковариации пропорциональны превышению эффективности ценных бумаг над безрисковыми вложениями (подразумевается, что последние на рынке имеются).

Задача 3. Рассчитайте среднюю ожидаемую доходность и среднеквадратическое отклонение операции Q, если

						-17
	0,25	0,18	0,12	0,05	0,03	0,02	0,2	0,15

Задача 4. Найдите детерминированный вариант процентной ставки, если момент ее начисления равномерно, распределен на временном отрезке [0,9; 1,8].

ариант 19

Вопрос 1. Оценка вклада ценной бумаги в общую ожидаемую эффективность портфеля.

Вопрос 2. Основной принцип хеджирования. Примеры.

Вопрос 3. Чем отличается форвардный контракт от фьючерсного контракта?

Вопрос 4. Основные предположения, принимаемые при построении модели оптимизации портфеля.

Задача 1. Рассчитайте среднюю ожидаемую доходность и среднеквадратическое отклонение операции Q, если

	0,2	0,18	0,32	0,1	0,2

Задача 2. Найдите математическое ожидание современной величины случайной ренты: платежи R осуществляются раз в год с равной вероятностью либо 1 октября, либо 1 декабря. Ставка равна i

Задача 3. С помощью компьютера найден оптимальный портфель Марковица для трех ценных бумаг с эффективностями и рисками: (5,9); (19,40); (40,80); нижняя граница доходности задана равной 26. Доли бумаг оказались равными: 36%, 28% ,36%. Определите риск и доходность для данного портфеля.

Задача 4. В начале года страховая компания кладет в банк 100 000 д.е. под 14 % годовых. В любой момент года возможен страховой случай, когда компании придется выплатить 50 000 д.е. страхового возмещения. Найдите математическое ожидание суммы на счете компании к концу года.

ариант 20

Вопрос 1. Методы снижения риска. Опционы.

Вопрос 2. Модель CAMP

Вопрос 3. Подсчет доходности вероятностных операций в условиях неопределенности.

Вопрос 4. Общее понятие детерминированного эквивалента финансового показателя

Задача 1. В начале года страховая компания кладет в банк 100 000 д.е. под 12 % годовых. В любой момент года возможен страховой случай, когда компании придется выплатить 100 000 д.е. страхового возмещения. Найдите математическое ожидание суммы на счете компании к концу года.

Задача 2. Найдите детерминированный вариант процентной ставки, если момент ее начисления равномерно, распределен на временном отрезке [0,8; 1,2].

Задача 3. Осуществляется одновременно множество инвестиционных проектов. Инвестиции в каждый проект равны 400 000, а будущий годовой доход случаен по проектам — равномерно распределен от 90 000 до 190 000 руб. Какая часть проектов окупится в течение 5 лет? (Процентная ставка 11% в год).

Задача 4. Статистика запросов кредитов в банке такова: 10% — государственные органы, 20% — другие банки и 70% — физические лица. Вероятности невозврата взятого кредита соответственно таковы: 0,01; 0,39 и 0,6. Найти вероятность невозврата очередного запроса на кредит (ответ округлить до тысячных).

ариант 21

Вопрос 1. Модель CAMP

Вопрос 2. Оценка вклада ценной бумаги в общую ожидаемую эффективность портфеля.

Вопрос 3. Плавающая ставка процента.

Вопрос 4. Диверсификация. Достоинства и недостатки этого метода.

Задача 1. Начальный капитал «челнока» равен 220 000 рублей. Опытные люди сказали ему, что в результате поездки за товаром и его последующей реализации капитал может с равной вероятностью возрасти в три раза, не измениться или уменьшиться в два раза (с вычетом со­путствующих издержек). Найти среднюю ожидаемую до­ходность планируемой операции.

Задача 2. Найдите детерминированный вариант процентной ставки, если момент ее начисления равномерно, распределен на временном отрезке [0,8; 1,5].

Задача 3. С помощью компьютера найден оптимальный портфель Марковица для трех ценных бумаг с эффективностями и рисками: (4,10); (10,40); (40,80); нижняя граница доходности задана равной 15. Доли бумаг оказались равными: 6%, 62% ,32%. Определите ожидаемую доходность для данного портфеля.

Задача 4. Статистика запросов кредитов в банке такова: 50% — государственные органы, 10% — другие банки и 40% — физические лица. Вероятности невозврата взятого кредита соответственно таковы: 0,01; 0,05 и 0,5. Найти вероятность невозврата очередного запроса на кредит.(ответ округлить до тысячных)

ариант 22

Вопрос 1. Статистически анализ финансового рынка. Однофакторная модель.

Вопрос 2. Подсчет доходности вероятностных операций в условиях неопределенности.

Вопрос 3. Кредитный риск и способы его уменьшения.

Вопрос4. Что означает отрицательная (положительная) корреляционная связь.

Задача 1. Запишем вариацию доходности портфеля в форме: и назовем величину портфельной ковариацией доходности 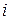-й ценной бумаги. Доказать, что в оптимальном портфеле эти ковариации пропорциональны превышению эффективности ценных бумаг над безрисковыми вложениями (подразумевается, что последние на рынке имеются).

Задача 2. Осуществляется одновременно множество инвестиционных проектов. Инвестиции в каждый проект равны 900 000, а будущий годовой доход случаен по проектам — равномерно распределен от 100 000 до 400 000 руб. Какая часть проектов окупится в течение 5 лет? (Процентная ставка 12% в год)

Задача 3. Пусть операции и некоррелированы, найдем риск операции (например, денег не хватит на проведение обеих операций в полном объеме):

	-50
0,2	0,8	0,7	0,3

Рассчитайте риск операции .

Задача 4. Запас золота в месторождении известен, как и начальные инвестиции в его разработку. Фактиче­ски полная отдача месторождения тоже фиксирована, следовательно, доходность (в процентах годовых) будет
зависеть от длительности выработки месторождения: чем дольше будет вырабатываться месторождение, тем больше доходность.

ариант 23

Вопрос 1. Модель CAMP

Вопрос 2. Основные предположения, принимаемые при построении модели оптимизации портфеля.

Вопрос 3. Диверсификация. Достоинства и недостатки этого метода.

Вопрос 4 Форвардная торговля. Примеры.

Задача 1. По договору в течение 15 лет в конце каждого квартала издательство переводит на счет автора случайную сумму денег (зависит от числа проданных книг). Предположим, что эта сумма равномерно распределена от 10 000 до 34 000 руб. Как найти современную величину этой ренты?

Задача 2. Сегодня днем цена акции равна 3 400 руб. За сутки цена может вырасти на 17% с вероятностью 3/6, с вероятностью 2/6 уменьшится в 3 раза и с вероятностью 1/6 остаться равной 3 400 руб. Найдите распределение цены акции завтра и послезавтра.

Задача 3. С помощью компьютера найден оптимальный портфель Марковица для трех ценных бумаг с эффективностями и рисками: (10,10); (20,40); (40,80); нижняя граница доходности задана равной 19. Доли бумаг оказались равными: 46%, 20% ,34%. Определите минимальный риск для данного портфеля.

Задача 4. Найдите детерминированный вариант процентной ставки, если момент ее начисления равномерно, распределен на временном отрезке [0,8; 1,3].

ариант 24

Вопрос 1. Статистически анализ финансового рынка. Однофакторная модель.

Вопрос 2. Общее понятие детерминированного эквивалента финансового показателя.

Вопрос 3. Плавающая ставка процента.

Вопрос 4. Рисковые инвестиционные процессы.

Задача 1. С помощью компьютера найден оптимальный портфель Марковица для трех ценных бумаг с эффективностями и рисками: (12,10); (34,40); (50,80); нижняя граница доходности задана равной 23. Доли бумаг оказались равными: 35%, 30% ,35%. Определите минимальный риск для данного портфеля.

Задача 2. Осуществляется одновременно множество инвестиционных проектов. Инвестиции в каждый проект равны 500 000, а будущий годовой доход случаен по проектам — равномерно распределен от 80 000 до 190 000 руб. Какая часть проектов окупится в течение 5 лет? (Процентная ставка 12,5% в год)

Задача 3. Найдите математическое ожидание современной величины случайной ренты: платежи R осуществляются раз в год с равной вероятностью либо 10 октября, либо 10 декабря. Ставка равна i

Задача 4. Пусть операции и некоррелированы, найдем риск операции (например, денег не хватит на проведение обеих операций в полном объеме):

	-5
0,3	0,7	0,65	0,35

Рассчитайте риск операции

ариант 25

Вопрос 1. Статистически анализ финансового рынка. Многофакторная модель.

Вопрос 2. Диверсификация. Достоинства и недостатки этого метода.

Вопрос 3. Подсчет доходности вероятностных операций в условиях неопределенности.

Вопрос 4. Общее понятие детерминированного эквивалента финансового показателя.

Задача 1. Рассчитайте среднюю ожидаемую доходность и среднеквадратическое отклонение операции Q, если

						-17
	0,25	0,18	0,12	0,05	0,03	0,02	0,2	0,15

Задача 2. Сегодня днем цена акции равна 33 000 руб. За сутки цена может вырасти на 17% с вероятностью 1/10, с вероятностью 4/10 уменьшится в 2,9 раза и с вероятностью 5/10 остаться равной 33 000 руб. Найдите распределение цены акции завтра и послезавтра.

Задача 3. С помощью компьютера найден оптимальный портфель Марковица для трех ценных бумаг с эффективностями и рисками: (9,4); (17,20); (30,60); нижняя граница доходности задана равной 25. Доли бумаг оказались равными: 25%, 30% ,45%. Определите риск и доходность для данного портфеля.

Задача 4. Найдите детерминированный вариант процентной ставки, если момент ее начисления равномерно, распределен на временном отрезке [0,7; 1,1].

ариант 26

Вопрос 1. Страхование. Достоинство и недостатки метода.

Вопрос 2. Финансовый риск в деятельности страховой компании.

Вопрос 3. Плавающая ставка процента.

Вопрос 4. Подсчет доходности вероятностных операций в условиях неопределенности.

Задача 1. Начальный капитал «челнока» равен 70 000 рублей. Опытные люди сказали ему, что в результате поездки за товаром и его последующей реализации капитал может с равной вероятностью возрасти в 2,5 раза, не измениться или уменьшиться в 1,9 раза (с вычетом со­путствующих издержек). Найти среднюю ожидаемую до­ходность планируемой операции.

Задача 2. Осуществляется одновременно множество инвестиционных проектов. Инвестиции в каждый проект равны 15 000, а будущий годовой доход случаен по проектам — равномерно распределен от 1500 до 90 000 руб. Какая часть проектов окупится в течение 7 лет? (Процентная ставка 9% в год)

Задача 3. В начале года страховая компания кладет в банк 100 000 д.е. под 12 % годовых. В любой момент года возможен страховой случай, когда компании придется выплатить 100 000 д.е. страхового возмещения. Найдите математическое ожидание суммы на счете компании к концу года.

Задача 4. С помощью компьютера найден оптимальный портфель Марковица для трех ценных бумаг с эффективностями и рисками: (9,7); (19,30); (35,50); нижняя граница доходности задана равной 18. Доли бумаг оказались равными: 46%, 20% ,34%. Определите минимальный риск для данного портфеля.

ариант 27

Вопрос 1. Оптимизация портфеля при возможности безрисковых вложений

Вопрос 2. Форвардная торговля. Примеры.

Вопрос 3. Основной принцип хеджирования. Примеры.

Вопрос 4. Общее понятие детерминированного эквивалента финансового показателя

Задача 1. По договору в течение 11 лет в конце каждого квартала издательство переводит на счет автора случайную сумму денег (зависит от числа проданных книг). Предположим, что эта сумма равномерно распределена от 10 000 до 24 000 руб. Как найти современную величину этой ренты?

Задача 2. Пусть операции и некоррелированы, найдем риск операции (например, денег не хватит на проведение обеих операций в полном объеме):

	-90
0,25	0,75	0,45	0,55

Рассчитайте риск операции .

Задача 3. С помощью компьютера найден оптимальный портфель Марковица для трех ценных бумаг с эффективностями и рисками: (19,10); (30,40); (70,80); нижняя граница доходности задана равной 45. Доли бумаг оказались равными: 16%, 40% ,44%. Определите минимальный риск для данного портфеля.

Задача 4. Запас золота в месторождении известен, как и начальные инвестиции в его разработку. Фактиче­ски полная отдача месторождения тоже фиксирована, следовательно, доходность (в процентах годовых) будет
зависеть от длительности выработки месторождения: чем дольше будет вырабатываться месторождение, тем больше доходность.

ариант 28

Вопрос 1. Статистически анализ финансового рынка. Однофакторная модель.

Вопрос 2. Чем отличается форвардный контракт от фьючерсного контракта?

Вопрос 3. Плавающая ставка процента.

Вопрос 4. Общее понятие детерминированного эквивалента финансового показателя.

Задача 1. Запишем вариацию доходности портфеля в форме: и назовем величину портфельной ковариацией доходности 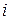-й ценной бумаги. Доказать, что в оптимальном портфеле эти ковариации пропорциональны превышению эффективности ценных бумаг над безрисковыми вложениями (подразумевается, что последние на рынке имеются).

Задача 2. Рассчитайте среднюю ожидаемую доходность и среднеквадратическое отклонение операции Q, если

	0,3	0,18	0,22	0,2	0,1

Задача 3. Найдите детерминированный вариант процентной ставки, если момент ее начисления равномерно, распределен на временном отрезке [0,6; 0,9].

Задача 4. Найдите математическое ожидание современной величины случайной ренты: платежи R осуществляются раз в год с равной вероятностью либо 11 октября, либо 11 декабря. Ставка равна i

ариант 29

Вопрос 1. Модель CAMP.

Вопрос 2. Диверсификация. Достоинства и недостатки этого метода.

Вопрос 3. Страхование. Достоинство и недостатки метода.

Вопрос 4. Финансовый риск в деятельности страховой компании.

Задача 1. По договору в течение 13 лет в конце каждого квартала издательство переводит на счет автора случайную сумму денег (зависит от числа проданных книг). Предположим, что эта сумма равномерно распределена от 30 000 до 120 000 руб. Как найти современную величину этой ренты?

Задача 2. Запишем вариацию доходности портфеля в форме: и назовем величину портфельной ковариацией доходности 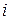-й ценной бумаги. Доказать, что в оптимальном портфеле эти ковариации пропорциональны превышению эффективности ценных бумаг над безрисковыми вложениями (подразумевается, что последние на рынке имеются).

Задача 3. Осуществляется одновременно множество инвестиционных проектов. Инвестиции в каждый проект равны 50 000, а будущий годовой доход случаен по проектам — равномерно распределен от 10 000 до 30 000 руб. Какая часть проектов окупится в течение 3 лет? (Процентная ставка 9% в год)

Задача 4. Рассчитайте среднюю ожидаемую доходность и среднеквадратическое отклонение операции Q, если

	0,4	0,18	0,32	0,1	0,1

ариант 30

Вопрос 1. Оценка вклада ценной бумаги в общую ожидаемую эффективность портфеля.

Вопрос 2. Основные предположения, принимаемые при построении модели оптимизации портфеля.

Вопрос 3. Форвардная торговля. Примеры.

Вопрос 4. Основной принцип хеджирования. Примеры.

Задача 1. Начальный капитал «челнока» равен 220 000 рублей. Опытные люди сказали ему, что в результате поездки за товаром и его последующей реализации капитал может с равной вероятностью возрасти в три раза, не измениться или уменьшиться в два раза (с вычетом со­путствующих издержек). Найти среднюю ожидаемую до­ходность планируемой операции.

Задача 2. Рассчитайте среднюю ожидаемую доходность и среднеквадратическое отклонение операции Q, если

	0,2	0,18	0,32	0,1	0,2

Задача 3. Найдите детерминированный вариант процентной ставки, если момент ее начисления равномерно, распределен на временном отрезке [0,8; 1,2].

Задача 4. С помощью компьютера найден оптимальный портфель Марковица для трех ценных бумаг с эффективностями и рисками: (14,10); (50,20); (70,50); нижняя граница доходности задана равной 35. Доли бумаг оказались равными:45%, 35% ,20%. Определите риск и доходность для данного портфеля.