Список литературных источников

ЛАБОРАТОРНАЯ РАБОТА № 3

Инстар и aутстар Гроссберга

Дисциплина: Информационные технологии

Номер группы: 3751

Выполнил: Гюлмамедов Турал Орхан оглы

Номер варианта: 2

Проверила: Павлова А.И

Дата регистрации на кафедре: «__»___________2015 г.

Новосибирск – 2015

Содержание:

1. Инстар и аутстар Гроссберга. Правило обучения нейрона по правилу Гроссберга.

2. Программный код обучения нейрона Matlab,C#

3. Результаты обучения (таблицы 1 и 2, рисунки работы консольного приложения)

Нейрон инстар и оутстар был введен С. Гроссбергом. Это взаимодополняющие элементы.

Нейрон типа инстар адаптирует веса сигналов, поступающих на сумматор нейрона к входным сигналам.

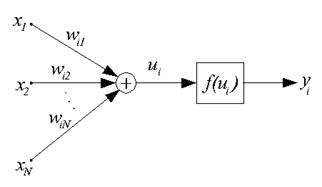
Рисунок 1 – Структура нейрона типа инстар

Входные сигналы, подаваемые с весовыми коэффициентами W_ij на вход i-го инстара, суммируются по формуле:

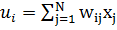, (1)

При обучении нейрона типа инстар часто используют линейную форму функции активации, при которойy_i = u_i.

Процесс обучения инстара производится по правилу, предложенному С. Гроссбергом, в соответствии с которым подбор весовых коэффициентов:

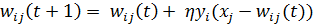, (2)

Входные данные в виде вектора xвыражаются в сети часто в нормализованном виде:

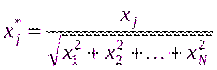, (3)

Результаты обучения по методу Гроссберга сильно зависят от коэффициента обучения сети η. При η =l веса w_ij становятся равными значениям Х_j уже после первой итерации. Ввод очередного входного вектора x вызовет адаптацию весов к новому вектору и полное «забывание» предыдущих значений.

При η <l в результате обучения w_ij весовые коэффициенты принимают усредненные значения вектораx.

Инстар может обучаться как с учителем, так и без него. При обучение без учителя в качестве значения принимается фактически значение выходного сигнала.

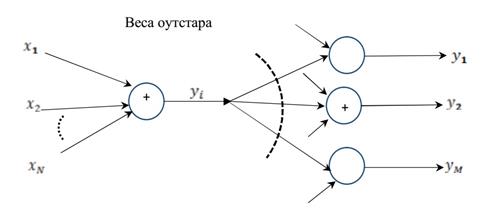
Рисунок 2 – Структура нейрона типа aутстар

Нейрон типа aутстар Гроссберга представляет собой комплементарное дополнение инстара. Если инстар обучается с целью распознать вектор, подаваемый на вход, то оутстар должен генерировать вектор, необходимый связанным с ним нейронам.

Оутстар является линейным нейроном. Процесс обучения заключается в таком подборе весовых коэффициентов W_ij, так чтобы выходные сигналы оутстара были равны ожидаемым значениям увзаимодействующих с ним нейронов.

Обучение aутстара производится по правилу Гроссберга:

W_ij (t+1) =W_ij (t) +η*Y_i*(Y_i-W_ij(t)),

где y_i – выходной сигнал i-го нейрона, выступающего в качестве источника.

При обучении инстара и оутстара Гроссберга весовые коэффициенты подстраиваются под входные или выходные векторы. Обучение может осуществляться как с учителем, так и без него.

Таблица 1– Результаты обучения нейрона модели инстар Гроссберга при коэффициенте обучения koeff= 0.5+0.01*2=0.52 и числе итераций iteration= 200+2=202

Входные данные	Весовые коэффициенты	Выходные данные
X	W=W+0.006 *2	Y
0 0 1 0 0 0 1 0 0 1 0 0 0 1 0 1 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1	0.312 0.212 0.312 0.612 0.512 0.312 0.312 0.412 0.112 0.212 0.612 0.312 0.412 0.312 0.112 0.512

Таблица 2– Результаты обучения нейрона модели инстар Гроссберга при коэффициенте обучения koeff= 0.8+0.01*2=0.82 и числе итераций iteration= 1000+4=1002

Входные данные	Весовые коэффициенты	Выходные данные
X	W=W+0.008*2	Y
0 0 1 0 0 0 1 0 0 1 0 0 0 1 0 1 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1	0.316 0.216 0.316 0.616 0.516 0.316 0.316 0.416 0.116 0.216 0.616 0.316 0.416 0.316 0.116 0.516

Программный код на Matlab

X=[0 0 1 0; 0 0 1 0; 0 1 0 0; 0 1 0 1; 1 0 0 0; 1 0 0 1; 1 0 1 0;1 0 1 1; 1 1 0 0; 1 1 0 1] % вектор входных данных

weight =[0.316 0.216 0.316 0.616; 0.516 0.316 0.316 0.416; 0.116 0.216 0.616 0.316; 0.416 0.316 0.116 0.516] % матрица синаптических весов

koeff= 0.82 % коэффициент скорости обучения сети от 0 до 1

itteration=1002 % количество итераций

for t=1:itteration

fori=1:10

forj=1:4

w(j)=X(i,:)* weight (j,:)' % результат суммирования, сумматор

end

[vc]=max(w) % отобразить значение максимального элемента и номера строки в матрице

% ' знак апострофа применяется для транспонирования матрицы

% правило Гроссбергадля инстара

weight (c,:)= weight (c,:)+koeff*(X(i,:)- weight (c,:))

% правилоГроссбергадляаутстара

% weight (c,:)= weight (c,:)+koeff*(Y(i,:)- weight (c,:))

% правило Гроссберга для аутстараcучителем

% weight (c,:)= weight (c,:)+koeff*Y*(Y(i,:)- weight (c,:))

%display(weight)% вывести результаты на экран

% нормализуем веса от 0 до 1 по формуле (3)

k=power(weight (c,:), 2); % возвести в квадрат

f=sqrt(sum(k)); % извлечь корень из суммы

weight (c,:)= weight (c,:)/f;

end

end

display(weight)

Реализация программы на С#

using System;

using System.Collections.Generic;

using System.Linq;

using System.Text;

using System.Threading.Tasks;

namespace InstarGrossbera

{

class Program

{

static void Main(string[] args)

{

double[,] X = new double[10, 4] { {0, 0, 1, 0}, //строки, столбцы

{0, 0, 1, 1},

{0, 1, 0, 0},

{0, 1, 0, 1},

{1, 0, 0, 0},

{1, 0, 0, 1},

{1, 0, 1, 0},

{1, 0, 1, 1},

{1, 1, 0, 0},

{1, 1, 0, 1}};

double[,] W = new double[4, 4] { {0.312, 0.212, 0.312, 0.612},

{0.512, 0.312, 0.312, 0.412},

{0.112, 0.212, 0.612, 0.312},

{0.412, 0.312, 0.112, 0.512}};

double koeff = 0.5+0.01*2;

double[] w = new double[4];

for (int k = 0; k < 202; k++)

{

for (int i = 0; i< 10; i++)

{

for (int j = 0; j < 4; j++)

{

w[j] = allRowValue(X, W, i, j);

}

int index = GetIndexMaxElement(w, w.Max());

redefinitionW(W, X, index, i, koeff);

}

}

Console.WriteLine("Weight = {");

for (int i = 0; i< 4; i++)

{

for (int j = 0; j < 4; j++)

{

Console.Write("\t" + Math.Round(W[i, j], 3, MidpointRounding.ToEven).ToString());

}

Console.Write("\n");

}

Console.WriteLine("\t}");

Console.ReadKey();

}

static double allRowValue(double[,] matrixA, double[,] matrixB,

int numberRowA, int numberRowB)

{

double a = 0;

for (int i = 0; i< 4; i++)

{

a += matrixA[numberRowA, i] * matrixB[numberRowB, i];

}

return a;

}

static int GetIndexMaxElement(double[] array, double maxElement)

{

for (int i = 0; i<array.Length; i++)

{

if (array[i] == maxElement)

return i;

}

return 0;

}

static void redefinitionW(double[,] W, double[,] X, int indexRow,

int indexRowX, double koeff)

{

double a = 0;

for (int i = 0; i< 4; i++)

{

W[indexRow, i] = W[indexRow, i] + koeff * (X[indexRowX, i] - W[indexRow, i]);

a += Math.Pow(W[indexRow, i], 2);

}

a = Math.Sqrt(a);

for (int i = 0; i< 4; i++)

{

W[indexRow, i] = W[indexRow, i] / a;

}

}

}

}

Рисунок 1 – Работа консольного приложения при коэффициенте обучения η =0.52 и числе итераций iteration=202

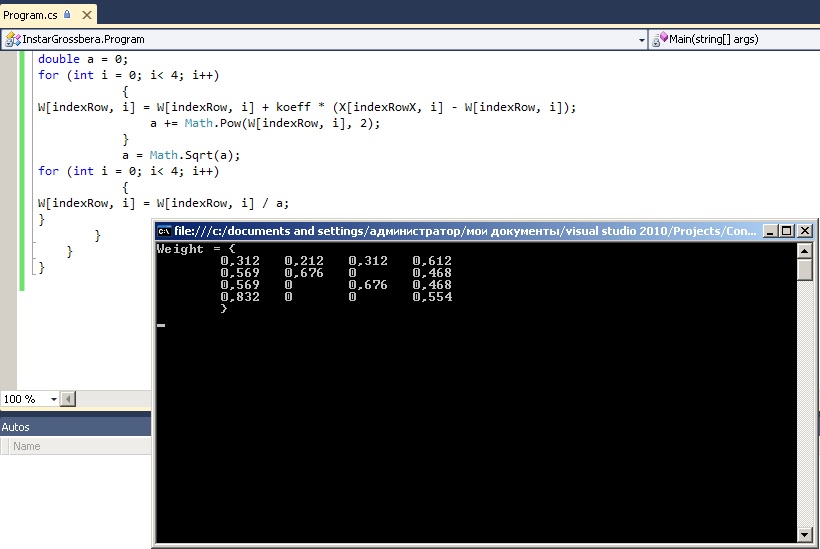
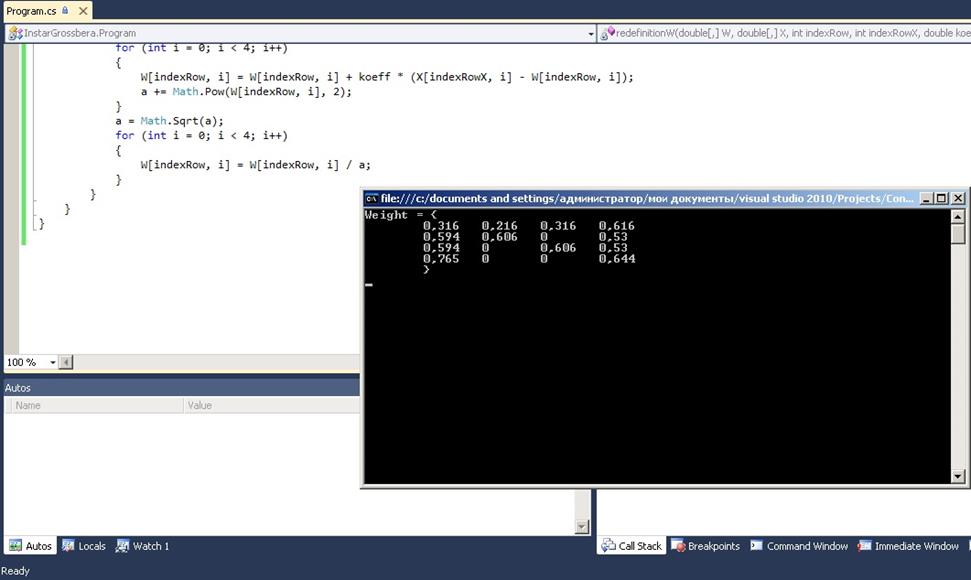
Рисунок 2 - Работа консольного приложения при коэффициенте обучения η =0.82 и числе итераций iteration=1002

Выводы

Был изученнейрон модели инстар Гроссберга. Результаты обучения по методу Гроссберга сильно зависят от коэффициента обучения сети η. При η =l веса w_ij становятся равными значениям Х_j уже после первой итерации. Ввод очередного входного вектора x вызовет адаптацию весов к новому вектору и полное «забывание» предыдущих значений. При η <l в результате обучения w_ij весовые коэффициенты принимают усредненные значения вектораx.

Список литературных источников

1. Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы: пер. с польского, И.Д. Рудинского. – М.: Горячая линия-Телеком, 2013. – 384 с.

2. ЛюгерДжорж Ф.Искусственный интеллект: стратегия и методы решения сложных проблем.- М.: Издательский дом Вильямс, 2003. – 864 с.

3. Осовский С. Нейронные сети для обработки информации / Пер. с польского. – М.: Финансы и статистика, 2002. – 342с.

4. Круглов В. В. Дли М. И. Голунов Р. Ю. Нечёткая логика и искусственные нейронные сети. – М.: Физматлит, 2001. – 221 с.

5. Уоссермен Ф. Нейрокомпьютерная техника. – М.: Мир, 1992. – 240 c.