Погашение задолженности по частям

Пусть ссуда в размере P, выданная на срок t, со ставкой начисления i с периодом начисления T, в течение срока ссуды t предусматривает два промежуточных платежа q₁ и q₂ в погашение задолженности. При этом возникают вопросы: Как определять при этом базу начисления процентов? Как определять остаток задолженности в конце срока?

Существуют два подхода к решению данных вопросов:

1. Актуарный метод.

2. Правило торговца.

Первый из них – актуарный метод – применяется при сроках больше года. Число дней в календарном году и сроки операции определяются по схеме 365/365. При поступлении платежей q₁ в погашение долга S = P + I₁, в первую очередь гасятся проценты

I₁ = P ´ i ´ t₁/T,

начисленные за период от начала срока ссуды до момента осуществления платежа t₁, а затем, если средств достаточно на погашение всех начисленных за этот период процентов

(q₁ – I₁) > 0,

погашается «тело» основной задолженности по ссуде

R₁ = P – (q₁ – I₁).

Фактическая задолженность R₁ служит в качестве базы для начисления процентов в следующем периоде (t₂ – t₁) до очередного платежа q₂ в погашение ссуды.

Контур операции по ссуде с двумя промежуточными платежами имеет вид:

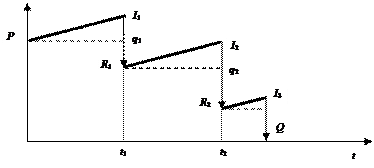Рис. 1.2

На рис. 1.2 по осям откладывается соответственно величина задолженности по ссуде (вертикальная ось) и время (горизонтальная ось).

В том случае, когда платеж q₁ не превосходит сумму процентов I₁, начисленных к моменту t₁ поступления платежа q₁, т.е.

(q₁ – I₁) < 0,

сумма поступившего платежа q₁ не идет в погашение начисленных процентов I₁ и не идет в погашение «тела» основной задолженности P, она учитывается при поступлении следующего платежа q₂, увеличивая его на величину q₁. Базой начисления процентов по ссуде до срока поступления платежа q₂ по-прежнему (до момента очередного платежа q₂) является исходная задолженность (в данном случае P).

Контур операции по ссуде с двумя промежуточными платежами q₁ и q₂ для случая, когда первый платеж q₁ не превышает величины процентов I₁, начисленных к дате t₁имеет вид рис. 1.3):

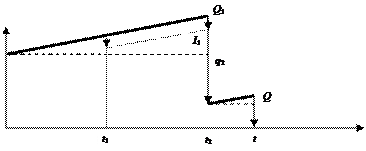Рис. 1.3

Окончательный платеж Q, осуществляемый в конце срока ссуды, должен погасить задолженность, т.е. «замкнуть» график контура операции (см. рис. 1.2, 1.3).

ПРИМЕР: Ссуда в размере 300 руб., выдана 10.02.2005 г. до конца года по ставке 18%. Задолженность по ссуде в течение срока ссуды погашалась четырьмя платежами 15.02.05 г. – 26 руб., 11.06.05 г. – 45 руб. , 01.09.06 г. – 60 руб. Определить сумму последнего платежа по ссуде:

Исходные данные	Дата	Число дней	Сумма поступления, руб.	База начисления, руб.	Начисленные проценты, руб.	Задолженность до поступления, руб.	Задолженность после поступления, руб.
Ссуда 300 руб.	10.02.00
365/360	15.02.00			300,00	0,75	300,75	274,75
Ставка 0,18	11.06.00			274,75	16,07	290,82.	245,82
01.09.00			245,82	10,08	255,90	195,90
31.12.00			195,90	11,85	207,75	207,75

Правило торговца обычно применяется на сроки задолженности меньше года. Начисления процентов по правилу торговца состоит в том, что база начисления процентов P (первоначальная сумма долга) остается неизменной в течение всего срока задолженности и проценты на нее начисляются за весь срок t по простой ставке i. Частичные платежи q в погашение ссуды учитываются в конце срока ссуды, причем учитываются с учетом начисления на суммы частичных платежей простых процентов по ставке ссуды i. Правило начисления простых процентов на частичные платежи q₁, q₂, q₃ в погашение ссуды такое же, как и начисление простых процентов на изменяющийся по величине депозит (см. (1.9)).

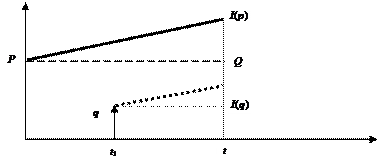Рис. 1.4

На рис. 1.4 приведен контур операции по ссуде P с одним промежуточным платежом q.

Окончательный платеж Q, осуществляемый в конце срока ссуды («замыкающий» график контура операции на рис. 1.4) определяется выражением

Q = (P + I(p)) – (q + I(q)).

ПРИМЕР: Ссуда в размере 500 руб., выдана на год (360/360) по ставке 15% с двумя промежуточными платежами в погашение 125 и 80 руб. в конце 4-го и 9-го месяцев. Определить сумму последнего платежа по ссуде.

Данные	Месяцы погашения	Срок в днях	Сумма процента, руб.	Сумма в погашение, руб.	Проценты по ссуде, руб.	Задолженность в конце срока ссуды, руб.
Ставка – 0,15
1-й платеж – 125 руб.			7,81	132,81
2-й платеж – 80 руб.			2,67	215,48		359,52
Ссуда – 500 руб.

ПРИМЕР 1. Определить коэффициент наращения по депозиту, размещенному по простой ставке 12% годовых на срок пять лет.

Решение: Коэффициент наращения – отношение наращенной суммы к исходной, т.е. депозиту. Наращенная сумма равна сумме депозита и начисленных процентов, начисленные проценты находятся как произведение депозита на значение ставки наращения, умноженные на отношение срока операции к периоду, на котором определена ставка наращения, т.е. k = (P + I)/P = (P + P ´ i ´ (t/T))/P = (1 + i ´ t/T) = 1 + 0,12*5 = 1,6.

ПРИМЕР 2. Коэффициент наращения по операции составил за два с половиной года 1,7. Какова ставка простых процентов по данной операции?

Решение: Коэффициент наращения равен k = (1 + i ´ t/T) откуда i = (k – 1) ´ T/t = 0,7/2,5 = 0,28, или 28%.

ПРИМЕР 3. Сколько времени потребуется для наращения 3 120 руб. до 4 630 руб. по простой ставке 5,6% годовых, схема (365/365).

Решение: Процентные деньги по данной операции равны S – P = 4 630 – 3 120 = 1 510 руб., с другой стороны I = i ´ P ´ t/T, откуда t = I ´ T/i ´ P = 1 510 ´ 365/0,056 ´ 3 120 = 3154 дня.

ПРИМЕР 4. Определить сумму долга, выданного под простую ставку 6,7% годовых, если в конце 4-го года кредитор получил 6 450 руб.

Решение: Сумма S, полученная кредитором, возросла по сравнению с займом на величину процентных денег S = P + I. Процентные деньги по данному займу составляют I = P ´ i ´ n. Таким образом, из выражения S = P + P ´ i ´ n можно найти исходную сумму займа P = S/(1 + i ´ n) = 6450/(1 + 0,067 ´ 4) = 1 752,71 руб.

Упражнения

1. Клиент разместил на депозите 1 450 руб. на срок 3 года с начислением процентов по простой ставке 15% годовых. Определить расходы банка по привлечению депозита.Ответ: 652,5 руб.

2. Определить величину ссуды, выданной под ставку 12,5% простых процентов, если по прошествии 2,5 лет заемщик уплатил 3 750 руб. Ответ: 2857,14 руб.

3. За какой период времени исходная величина долга возрастет в два раза при простой ставке обыкновенного процента 23% годовых. Ответ: 1565 дней.

4. Определить величину простой процентной ставки, если за 27 месяцев коэффициент наращения по операции равен 1,36. Ответ: 16%.

5. Чему равен коэффициент наращения по ссуде величиной 3750 руб., выданной на 6 лет, если ставка по ссуде 14,5% в конце 2-го года увеличилась на 2,5 процентных пункта. Ответ: 1,97.

6.Определить доходы банка по депозитной операции сроком 8 лет и простой ставке 13%, если в середине срока величина депозита в 2 560 руб. возросла в полтора раза.Ответ: 3328 руб.

7. Сравните выгодность для заёмщика двух финансовых операции: займ сроком 4,5 года при простой ставке в 17% годовых и ссуда с простой ставкой в 432 дня с общим коэффициентом наращения по операции 1,35. Ответ: цена средств по займу меньше на 12,57 процентных пунктов.

8. Чему равен окончательный платеж в погашение задолженности размером 9 405 руб., выданной на срок 49 месяцев под простую ставку 13,5% годовых, если через полтора года был осуществлен промежуточный платеж в размере 220 руб. Ответ 14490,17 руб.

9. На какую величину снизится завершающий платеж по годовой задолженности в 7 805 руб. выданный под простую ставку 23,5%, если в начале третьего квартала заемщик выплатил кредитору 500 руб. Ответ: 29,37 руб.

10. На сколько окончательный платеж рассчитанный по правилу торговца больше окончательного платежа, рассчитанного по актуарному методу для задолженности размером 6 500 руб. со сроком 6 месяцев с промежуточным платежом 1 700 руб. в конце первого месяца и простой ставкой по задолженности 16% годовых. Ответ:59,37 руб.

ВОПРОСЫ:

1. Наращение, процентные деньги, процентная ставка, коэффициент наращения.

2. Временная база процентной ставки. Различия в определении годовой базы. Правила исчисления дней в году и времени операции.

3. Наращение по правилу простых процентов. База начисления простых процентов. Коэффициент наращения при наращении по правилу начисления простых процентов.

4. Начисление простых процентов за произвольный период времени.

5. Начисление простых процентов m раз на периоде временного основания простой ставки наращения.

6. Начисление простых процентов при изменяющейся ставке. Коэффициент наращения.

7. Начисление простых процентов при изменении базы начисления, процентное число, процентный делитель.

8. Погашение задолженности по частям. Методы погашения задолженности с промежуточными платежами.

9. Актуарный метод погашения задолженности с промежуточными платежами.

10. Правило торговца при погашении задолженности.

11. Отличие актуарного способа погашения задолженности частями от правила торговца.

Лекция 2