Развитие результатов Г. Марковица в трудах Д. Тобина
Влияние теории Марковица значительно усилилось после появления в конце 50-х годов работ Тобина по аналогичной тематике, но имеющих другой подход. В работах Тобина основной темой становится анализ факторов, побуждающих инвесторов формировать портфели активов вместо держания капитала в какой-то одной форме (например, налично-денежной). Поэтому Тобин включил в анализ безрисковые активы и главной задачей и в теории, и на практике считал оптимальное распределение капитала между безрисковыми и рисковыми вложениями.
Если инвестор распределил капитал между безрисковыми и рисковыми активами в пропорциях: 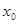 - в безрисковые,
- в безрисковые, 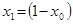 - в рисковые, то ожидаемая доходность его капитала (портфеля) определяется:
- в рисковые, то ожидаемая доходность его капитала (портфеля) определяется:
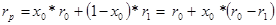 , (2.9)
, (2.9)
где 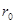 - доходность безрисковой, а
- доходность безрисковой, а 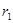 - ожидаемая доходность рисковой части портфеля.
- ожидаемая доходность рисковой части портфеля.
Риск такого портфеля определяется только его рисковой частью:
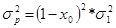 , (2.10)
, (2.10)
где 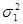 - дисперсия доходности рисковой части портфеля.
- дисперсия доходности рисковой части портфеля.
Используя (2.9) и (2.10) , после исключения 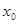 получаем:
получаем:
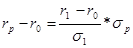 . (2.11)
. (2.11)
(2.11) показывает линейную зависимость доходности портфеля сверх гарантированного значения и риска портфеля.
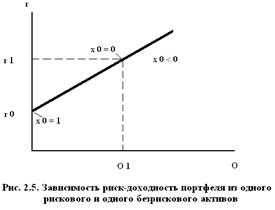
Поведение инвестора, формирующего оптимальный портфель из рисковой и безрисковой частей, удобно представить графически на плоскости 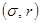 - рис.2.5.
- рис.2.5.
Если инвестору даны только один рисковый и один безрисковый актив, то все варианты распределения капитала в соответствии с (2.11) отображаются отрезком прямой линии (рис.2.5). Точка 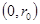 соответствует вложению всего капитала в безрисковый актив при
соответствует вложению всего капитала в безрисковый актив при 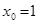 , точка
, точка 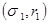 - вложению только в рисковый актив при
- вложению только в рисковый актив при 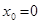 . Все промежуточные варианты соответствуют внутренним точкам отрезка, а возможность заимствования средств ( по безрисковой ставке) с их вложением в рисковый актив соответствует продолжению прямой вправо при
. Все промежуточные варианты соответствуют внутренним точкам отрезка, а возможность заимствования средств ( по безрисковой ставке) с их вложением в рисковый актив соответствует продолжению прямой вправо при 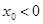 .
.
Характер зависимости не изменится , если считать, что рисковым активом является какой-то портфель рисковых ценных бумаг. На рис.2.6 представлен эффективный фронт некоторой совокупности рисковых ценных бумаг, из точек которого инвестор выбирает оптимальный портфель в соответствии со своей склонностью к риску и без учета возможности безрискового инвестирования. Рассмотрим две точки А и Сна этом эффективном фронте по Марковицу, но с учетом возможности безрискового вложения. Пусть оптимальному портфелю инвестора, составленному только из рисковых активов, соответствовала точка А. Перераспределение средств в пользу безрискового актива, но с сохранением структуры рисковой части вызовет, как и ранее, перемещение местоположения портфеля влево по отрезку АR. Но очевидно, что ни сама точка А, ни отрезок АR не представляют более эффективные портфели, поскольку можно составить портфель с тем же уровнем риска, но более доходный, используя комбинацию безрискового актива и рисковой части, имеющей структуру портфеля С (на рис. 2.6 портфель A'предпочтительнее А, поскольку 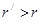 при одинаковом
при одинаковом 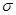 ).
).
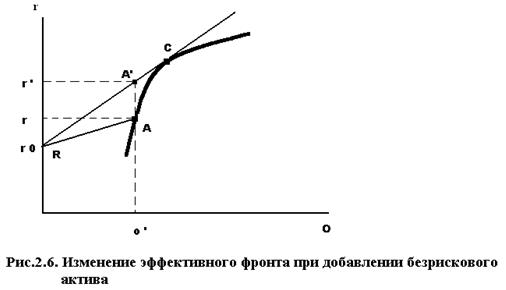
Сказанное относится ко всем портфелям, представленным на эффективном фронте по Марковицу ниже и левее точки С, и таким образом, эта часть эффективного фронта заменяется отрезком RC. А при возможности заимствования инвестор по тем же причинам предпочтет продолжение отрезка RCвправо от точкиС.В результате эффективный фронт будет представлен прямой, включающей единственную точку С из эффективного фронта Марковица.
Точка С представляет так называемый касательный портфельи имеет очень важное значение в построениях Тобина. Во-первых, это точка касания эффективного фронта Марковица с прямой, проведенной из точки безрисковой доходности R. Во-вторых, эта касательная имеет самый большой угол наклона к оси абсцисс среди всех прямых, проведенных из точки R к эффективному фронту Марковица. Последнее на содержательном уровне интерпретируется так: инвесторы, более "осторожные" чем выбравшие точку Св качестве оптимальной по Марковицу, будут формировать свой оптимальный портфель из безрискового актива и рисковой части, причем структура рисковой составляющей будет аналогична структуре касательного портфеля. Это положение существенно отличается от вывода Марковица, поскольку инвесторы с разной склонностью к риску (в указанных пределах) формируют рисковую часть портфеля одинаково по структуре. Но тогда инвестор при составлении оптимального портфеля будет действовать в два этапа:
1. Нахождение структуры касательного портфеля .
2. Распределение капитала между касательным портфелем и безрисковым активом в соответствии с индивидуальной склонностью к риску.
Возможность раздельного решения задач оптимизации рисковой части портфеля и портфеля в целом известно как теорема о разделении .
К тем же выводам приводит и формальное математическое решение задачи Тобина, приведенное, например в [3, стр.109-113] (рассмотрены случаи привлечения займов и без них). Кроме классических формальных методов решения задачи Тобина существуют "специализированные", основанные на использовании теоремы о разделении, т.е. на первоначальном нахождении касательного портфеля. Например, можно использовать уже упоминавшийся метод критических линий или описанный в [4, стр.253-256 ] метод EGP, названный по именам создателей Элтона, Грубера и Падберга (метод использует свойство касательного портфеля иметь максимальный угол наклона прямой, соединяющей соответствующую ему точку с точкой безрисковой доходности).
Макроэкономическое значение результатов Тобина состоит в моделировании спроса на деньги при изменении доходности рисковых активов.
Хотя предположение Тобина о возможности чисто безрисковых вложений на практике строго не выполнимо, решение задачи Тобина с использованием слаборисковых активов оказывается близким к расчетному и поэтому имеет практическое значение [3, стр.112] .
