Метода группировок и метода средних 8 страница
| hi | ||||||||||||
| Hhi |
где i – номер промежутка от i-го часа до (i +1)-го, i = 0,1,…,11, а hi – число часов, показания которых принадлежат i-му промежутку.
ВЫЧИСЛИТЕ выборочные среднюю и дисперсию, а также выборочные доли отдельных значений признаков. ПОСТРОЙТЕ гистограмму и полигон относительных частот данного интервального ряда распределения.
ЗАДАЧА 260
Для определения точности измерительного прибора, систематическая ошибка которого практически равна нулю, было проведено пять независимых измерений. Их результаты представлены таблицей:
| i | |||||
| xi |
где i – номер измерения, а xi – соответствующий результат измерения в метрах.
ОПРЕДЕЛИТЕ несмещённую оценку дисперсии ошибок измерительного прибора, если значение измеряемой величины: а) известно и равно 2800 м; б) неизвестно.
ЗАДАЧА 261
Даны две выборки объёмом n1 и n2. Для них найдены средние арифметические (` х1 и `х2 ) и две выборочные дисперсии ( S12 и S22 ). Указанные выборки были объединены и для вновь получившейся выборки найдены общая средняя `х и дисперсия S2. ВЫРАЗИТЕ `х и S2 через характеристики двух выборок.
ЗАДАЧА 262
НАЗОВИТЕ основные теоремы теории вероятностей, которые обеспечивают несмещённость выборочной средней и выборочной доли.
ЗАДАЧА 263
ЗАПИШИТЕ доверительные интервалы для генеральной средней и доли с вероятностями 0,95 и 0,99. ДАЙТЕ статистическую интерпретацию доверительных интервалов. От чего зависит точность оценки параметров генеральной совокупности – генеральной средней и генеральной доли?
ЗАДАЧА 264
Методом повторной случайной выборки в районе определяется доля коров с суточным удоем, превышающим 12 кг молока. Из обследованных 800 коров суточный удой 320 коров составил более 12 кг.
ОПРЕДЕЛИТЕ:
1) среднюю ошибку выборочной доли этих коров в целом по району;
2) с вероятностью 0,954 – предельную ошибку доли коров с суточным удоем, превышающим 12 кг, во всём районе;
3) с вероятностью 0,954 – доверительный интервал доли этих коров в целом по району.
ЗАДАЧА 265
Для определения средней продолжительности горения электроламп из партии в 100 тысяч шт. в порядке случайной бесповторной выборки обследовано 200 шт.
С вероятностью 0,997 ВЫЧИСЛИТЕ:
1) предельную ошибку средней продолжительности горения всех электроламп, если среднеквадратическое отклонение продолжительности горения обследованных электроламп составило 100 часов;
2) доверительный интервал для средней продолжительности горения всех электроламп, если средняя продолжительность горения 200 обследованных электроламп составила 980 часов.
ЗАДАЧА 266
ЧЕМ отличается величина средней квадратической ошибки простой случайной выборки при повторном и бесповторном отборе. КАКАЯ из этих ошибок больше? ПРИ КАКИХ условиях различиями между этими двумя формами выборки можно пренебречь?
ЗАДАЧА 267
В корпорации работает 1000 рабочих. Было проведено выборочное обследование рабочих по возрасту. Методом случайного бесповторного отбора обследовались 50 человек. Получены следующие результаты обследования:
| Возраст рабочих, лет | до 30 | 30-40 | 40-50 | 50-60 | 60 и выше |
| Число рабочих |
С вероятностью 0,997 ОПРЕДЕЛИТЕ пределы, в которых находится средний возраст рабочих корпорации.
ЗАДАЧА 268
В порядке механической выборки было подвергнуто испытанию на разрыв 100 нитей из партии пряжи. В результате обследования установлено, что средняя крепость пряжи составила 320 г при среднем квадратическом отклонении 20 г. С вероятностью 0,954 ОПРЕДЕЛИТЕ пределы, в которых находится средняя крепость пряжи в партии.
ЗАДАЧА 269
По результатам 1%-ного выборочного обследования вкладчиков Сбербанка микрорайона методом бесповторного отбора получено следующее распределение вкладчиков по размеру вклада (в усл. ден. ед.):
| Размер вклада | До 300 | 300-600 | 600-900 | 900-1200 | 1200-1500 | Выше 1500 |
| Число вкладчиков |
ОПРЕДЕЛИТЕ пределы среднего размера вкладов в Сбербанк микрорайона: а) с вероятностью 0,954; б) с вероятностью 0,997.
ЗАДАЧА 270
С целью характеристики среднего размера вкладов населения города проведена бесповторная случайная 10%-ная выборка вкладчиков банков, в результате которой получено следующее распределение вкладчиков по размеру вкладов:
| Размер вклада ден. ед. | До 500 | 500-1000 | 1000-1500 | 1500-2000 | и выше | Итого |
| Число вкладчиков |
ОПРЕДЕЛИТЕ:
1) с вероятностью 0,997 пределы, в которых можно ожидать средний размер вклада всех вкладчиков города;
2) с вероятностью 0,954 возможные пределы доли вкладчиков с размером вклада более 2000 ден. ед. среди всех вкладчиков города?
ЗАДАЧА 271
Для зоотехнического обследования живой массы коров, среднего годового удоя и процента жирности молока в порядке бесповторной случайной выборки обследуется 100 коров из 1000 коров. Средние квадратические отклонения указанных признаков для обследованных 100 коров (попавших в выборку) соответственно оказались равными 110 кг, 600 кг и 0,2%. ОПРЕДЕЛИТЕ с вероятностью 0,954 предельные ошибки среднего значения каждого из этих трёх признаков.
ЗАДАЧА 272
По результатам решения предыдущей задачи ОПРЕДЕЛИТЕ пределы, в которых будут находиться средние значения рассматриваемых признаков для всей совокупности коров, если для 100 обследованных коров средняя масса равна 400 кг, средний годовой удой 2800 кг, а средний процент жирности молока 3,9.
ЗАДАЧА 273
Производится выборочная 5%-ная разработка данных об успеваемости студентов дневной формы обучения вуза по результатам зимней экзаменационной сессии. Получены следующие данные об успеваемости:
| Баллы | Всего | ||||
| Число студентов |
Принимая во внимание, что отбор был случайным и бесповторным, ОПРЕДЕЛИТЕ с вероятностью 0,954 по вузу в целом: а) предельную ошибку выборки среднего выборочного балла успеваемости; б) пределы, в которых находится средний балл успеваемости.
ЗАДАЧА 274
Каков должен быть объём выборки (число обследованных студентов) в условиях предыдущей задачи, чтобы предельная ошибка при определении доли студентов, имеющих неудовлетворительную оценку, не превысила 2%?
ЗАДАЧА 275
Для определения средней продолжительности телефонных разговоров по городской сети в порядке случайной повторной выборки обследовано 100 телефонных разговоров. При этом было установлено, что среднее квадратическое отклонение по длительности разговора равно 1,4 мин. Какова вероятность того, что предельная ошибка при определении средней продолжительности телефонных разговоров не превышает 25 с.?
ЗАДАЧА 276
Для определения средней влажности пшеницы проводится случайная бесповторная выборка. Сколько проб весом 200 г необходимо взять для того, чтобы с вероятностью 0,997 гарантировать ошибку средней влажности всего зерна, не превышающую 0.1%? Среднее квадратическое отклонение по данным прошлого обследования равно 0,6%.
ЗАДАЧА 277
Методом случайного бесповторного отбора из населения города А, насчитывающего 2 тысячи семей, выбраны 80 семей. В результате их обследования установлено, что 24 семьи состоят из четырёх и более человек. ОПРЕДЕЛИТЕ пределы, в которых находится доля семей, состоящих из четырёх и более человек, с вероятностью 0,954.
ЗАДАЧА 278
Из пяти тысяч человек, совершивших правонарушения в течение года, методом механического отбора были выделены 500 правонарушителей. В результате их обследования установлено, что 300 человек выросли в нормальных семейных условиях. С вероятностью 0,997 ОПРЕДЕЛИТЕ долю правонарушителей, выросших в неблагополучных семьях.
ЗАДАЧА 279
При обследовании 500 образцов изделий, отобранных из партии готовой продукции предприятия в случайном порядке, оказалось 40 нестандартных. С вероятностью 0,954 ОПРЕДЕЛИТЕ пределы, в которых находится доля нестандартной продукции, выпускаемой предприятием.
ЗАДАЧА 280
В порядке случайной повторной выборки было обследовано 80 предприятий одной отрасли промышленности, из которых 20 предприятий имели долю бракованной продукции свыше 0,5%. С вероятностью 0,997 ОПРЕДЕЛИТЕ пределы, в которых находится доля предприятий, выпускающих более 0,5% бракованной продукции данной отрасли.
ЗАДАЧА 281
В порядке случайной повторной выборки было отобрано 400 единиц готовой продукции предприятия, из которых 20 единиц было забраковано. С вероятностью 0,954 ОПРЕДЕЛИТЕ пределы, в которых находится доля бракованной продукции предприятия.
ЗАДАЧА 282
Для решения каких вопросов организации выборочного наблюдения и оценки его результатов может использоваться формула средней квадратической ошибки выборки?
ЗАДАЧА 283
В районе проживает 100 тысяч семей. Из них 50 тысяч семей рабочих, 40 тысяч семей сельских жителей и 10 тысяч семей служащих. При обследовании числа детей в семье были получены следующие данные:
| Типы семей | Число семей в генеральной совокупности | Среднее число детей в семье | Среднее квадратическое отклонение |
| Рабочие | 50 000 | 2,2 | 2,4 |
| Сельские жители | 40 000 | 2,9 | 3,1 |
| Служащие | 10 000 | 1,6 | 0,9 |
Для выборки объема n=50 ВЫЧИСЛИТЕ объемы выборок nj в каждом слое при:
1) равномерном размещении единиц;
2) пропорциональном размещении единиц;
3) оптимальном размещении единиц.
СРАВНИТЕ эффективность выборок при оценивании среднего числа детей в семье.
ЗАДАЧА 284
В таблице приведены данные о средней удойности коров некоторой области по районам:
| Район | Число коров, тыс. голов | Средний удой коров, л | Среднее квадратическое отклонение |
| I | |||
| II | |||
| III | |||
| IV |
Для выборки объема n=300 ВЫЧИСЛИТЕ объемы выборок в каждом слое при:
1) пропорциональном размещении единиц;
2) оптимальном размещении единиц.
СРАВНИТЕ эффективность этих методов.
ЗАДАЧА 285
С целью определения доли брака во всей парии изготовленных деталей была проведена 10%-ная расслоенная выборка с отбором единиц пропорционально численности единиц однородных групп. Внутри групп применялся метод бесповторного отбора. Результаты выборки представлены в таблице:
| Типы станков | Выработка одного станка, шт. | Процент брака по данным выборки |
| 2,0 | ||
| 3,0 | ||
| 1,5 | ||
| 1,0 | ||
| 1,8 |
С вероятностью 0,997 ОПРЕДЕЛИТЕ предел, в котором находится доля брака во всей партии деталей, изготовленных на всех станках.
ЗАДАЧА 286
Для определения затрат времени на обработку деталей рабочими разных квалификаций на заводе была произведена 10%-ная расслоенная выборка пропорционально численности выделенных групп по методу случайного бесповторного отбора данных о затратах времени на обработку одной детали. Результаты представлены в таблице:
| Группы рабочих по квалификации | Число рабочих в выборке | Средние затраты времени на обработку одной детали, мин. | Среднее квадратическое отклонение |
| I | |||
| II | |||
| III | |||
| IV |
С вероятностью 0,954 ОПРЕДЕЛИТЕ пределы, в которых находятся средние затраты времени на обработку деталей рабочими завода.
ЗАДАЧА 287
С целью проверки качества электроламп проведена 5%-ная серийная случайная бесповторная выборка из партии изделий в 10000 шт. Электролампы упакованы в коробки по 50 шт. в каждом. Средняя продолжительность горения электроламп составила 1030 ч, а межгрупповая дисперсия – 170 ч. С вероятностью 0,954 ОПРЕДЕЛИТЕ: а) предельную ошибку средней продолжительности горения электроламп; б) доверительный интервал для средней продолжительности горения электроламп во всей партии.
ЗАДАЧА 288
С целью проверки веса пачек макаронных изделий с помощью серийной бесповторной выборки обследовано 10 ящиков из партии в 300 ящиков. Результаты наблюдения представлены в таблице:
| N ящика | ||||||||||
| Средний вес пачки в ящике, г |
С вероятностью 0,954 ОПРЕДЕЛИТЕ: а) в каких пределах колеблется средний вес пачек с макаронными изделиями во всей партии; б) сколько ящиков должно быть обследовано, чтобы ошибка не превышала 20 г, на основе приведенных выше данных.
ЗАДАЧА 289
Для определения средней длины детали необходимо провести выборочное обследование методом случайного повторного отбора. КАКОЕ количество деталей необходимо отобрать, чтобы ошибка выборки не превышала 2 мм с вероятностью 0,954 при среднем квадратическом отклонении 8 мм?
ЗАДАЧА 290
Для установления среднего возраста 50 тыс. читателей библиотеки необходимо провести выборку из читательских карточек методом механического отбора. Предварительно установлено, что среднее квадратическое отклонение возраста читателей равно 10 годам. ОПРЕДЕЛИТЕ необходимую численность выборки при условии, что с вероятностью 0,954 ошибка выборки будет не более двух лет.
ЗАДАЧА 291
Необходимо установить средний стаж работы 10 тыс. заводских рабочих, используя метод механической выборки. Предварительное обследование показало, что среднее квадратическое отклонение по стажу работы равно 5 годам. ОПРЕДЕЛИТЕ минимально возможный объём выборки.
ЗАДАЧА 292
В городе А предполагается определить среднее число детей на семью методом случайного повторного отбора. КАКОВ должен быть объём выборки, чтобы с вероятностью 0,997 ошибка выборки не превышала 1 человека, если на основе предыдущ их обследований известно, что дисперсия равна 9?
ЗАДАЧА 293
На заводе с числом рабочих 15 тысяч человек методом механической выборки предполагается определить долю рабочих со стажем работы до 20 лет и более. КАКОВА должна быть численность выборки, чтобы с вероятностью 0,954 ошибка выборки не превышала 0,03, если на основе предыдущих обследований установлено, что дисперсия равна 0,2?
ЗАДАЧА 294
В городе N, где проживает 10 тысяч семей, методом случайного бесповторного отбора предполагается определить долю семей с детьми до трёх лет. КАКОВ должен быть объём выборки, чтобы с вероятностью 0,954 ошибка выборки не превышала 0,04, если на основе предыдущих обследований известно, что дисперсия равна 0,24? Изменится ли объём выборки при условии, что метод отбора повторный?
ЗАДАЧА 295
На заводе с числом рабочих 15 тысяч методом механического отбора необходимо установить долю рабочих, обучающихся в высших учебных заведениях. КАКОВ должен быть объём выборки, чтобы с вероятностью 0,997 ошибка выборки не превышала 0,08, если на основе предыдущих обследований известно, что дисперсия равна 0,16?
ЗАДАЧА 296
НАЙДИТЕ формулы для вычисления объема выборки n, если оцениваются доля и число единиц с определенным значением признака в случае:
4) равномерного размещения единиц выборки;
5) пропорционального размещения единиц выборки по слоям;
6) оптимального размещения единиц выборки.
ЗАДАЧА 297
Результаты сплошного учёта скота в различных видах хозяйств района на 1 января 2001 г. и результаты 10%-ного контрольного обхода в этом районе характеризуются данными, представленными в таблице. Скорректируйте данные сплошного наблюдения по результатам контрольного обхода и установите поголовье скота по видам на 1 января 2001 года.
| Виды скота | Общая численность скота в районе по данным сплошного учёта, гол. | Численность скота в хозяйствах, охваченных контрольным обходом, гол. | |
| по данным сплошного учёта | по данным контрольного учёта | ||
| Крупный рогатый скот Овцы Свиньи |
Тема 10. ИЗУЧЕНИЕ ЗАВИСИМОСТИ НА ОСНОВЕ СОЧЕТАНИЯ
МЕТОДА ГРУППИРОВОК И МЕТОДА СРЕДНИХ
Один из наиболее распространенных методов изучения связей - метод группировок в сочетании с методом средних. Этот метод позволяет установить наличие связи, определить направление связи, приближенно измерить тесноту связи.
Методика применения группировок в сочетании со средними при изучении связей заключается в следующем:
1) проводят группировку изучаемой совокупности по величине факторного признака;
2) рассчитывают среднее значение результативного признака для каждой группы;
3) сопоставляют направление изменения среднего значения результативного признака с направлением изменения факторного признака.
Если значения факторного и результативного признаков изменяются в одном направлении, то связь прямая. Если они изменяются в противоположных направлениях, то связь обратная. Если с увеличением факторного признака среднее значение результативного то уменьшается, то увеличивается, то связь между признаками отсутствует.
Например, если группировать рабочих по тарифному разряду и рассчитывать среднюю выработку для каждой группы, то можно установить наличие прямой связи между этими признаками: с ростом квалификации рабочих увеличивается и средняя выработка.
Рассматриваемый метод позволяет измерить тесноту связи. Для этого используют показатели вариации результативного признака: общую дисперсию (s2) и межгрупповую дисперсию (d2). Методика расчета этих показателей рассматривается в теме 5 «Показатели вариации».
Общая дисперсия показывает вариацию результативного признака, вызванную всеми действующими на нее факторами:
s2 = 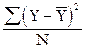 ,
,
где Y - отдельное значение результативного признака; 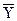 - среднее значение
- среднее значение
результативного признака; N - число единиц в совокупности.
Межгрупповая дисперсия характеризует вариацию результативного признака, вызванную признаком-фактором, положенным в основание группировки:
d2 = 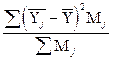 ,
,
где 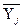 - среднее значение результативного признака в j-й группе;
- среднее значение результативного признака в j-й группе; 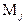 - число
- число
единиц в j-й группе.
Разделив межгрупповую дисперсию на общую, получим эмпирический коэффициент детерминации:
hэ2= 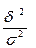 .
.
Его значения находятся в пределах: 0≤hэ2≤1.
Эмпирический коэффициент детерминации показывает, какая доля вариации результативного признака вызвана признаком, положенным в основание группировки. Так, если hэ2 = 0,685 или 68,5%, то это значит, что вариация результативного признака на 68,5% обусловлена влиянием признака, положенного в основание группировки, и на 31,5% - влиянием всех прочих факторов. Чем больше эта доля, тем сильнее влияние факторного признака на результативный. Поэтому коэффициент детерминации используется как показатель тесноты связи между факторным и результативным признаком. При hэ2 = 0 связь между признаками отсутствует. При hэ2 = 1 связь функциональная, вся вариация вызвана группировочным признаком.
В качестве показателя тесноты связи используют также эмпирическое корреляционное отношение, представляющее собой квадратный корень из коэффициента детерминации:
hэ = 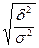 .
.
Его значения также находятся в пределах: 0≤hэ≤1.
Чем ближе корреляционное отношение к 0, тем связь слабее; чем ближе оно к 1, тем связь теснее.
Принято считать, что если hэ>0,5, то связь заметная, если hэ>0,7, - то высокая, если hэ>0,9, - то весьма высокая.
Когда установлено, что связь высокая, можно продолжать исследование зависимости признаков нахождением линии регрессии.
Рассмотрим решение задачи на исследование зависимости производительности труда от энерговооруженности труда.
Задача.
Имеем информацию по 25 промышленным предприятиям региона:
| № п/п | Энерговооруженность труда, кВт.ч (Х) | Производительность труда, шт. (Y) |
| 7,1 7,2 7,9 8,3 8,5 9,0 9,3 9,6 9,7 10,2 10,5 11,0 11,6 12,3 12,4 12,6 12,8 13,2 13,4 13,7 13,8 14,0 14,1 14,3 14,4 |
ОПРЕДЕЛИТЕ:
1) наличие и направление связи между производительностью труда и его энерговооруженностью;
2) тесноту связи между исходными признаками.
сделайте выводы.
РЕШЕНИЕ:
1. Установим наличие и направление зависимости производительности труда от энерговооруженности труда с помощью аналитической группировки изучаемой совокупности: 25 предприятий разобьем на 5 групп с равным интервалом по величине факторного признака (Х).
1.1. Находим размер интервала (i) следующим образом:
i = R/n,
где R - размах вариации, который определяется как разность между максимальным и минимальным значениями признака; n - установленное число групп (определяется либо по формуле Стерджесса, либо устанавливается исследователем).
В нашем случае
i = 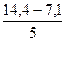 =1,46»1,5(кВт.ч).
=1,46»1,5(кВт.ч).
1.2. Далее установим полную шкалу интервалов по методологии, изложенной в теме 1 «Сводка и группировка статистических материалов».
1.3. Подсчитаем число предприятий, входящих в каждую группу.
1.4. Рассчитаем средние уровни производительности труда в каждой группе и в целом по совокупности:
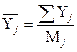 ,
,
где 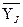 - среднее значение результативного признака для каждой j-й группы;
- среднее значение результативного признака для каждой j-й группы; 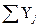 -сумма значений результативного признака; Mj – число предприятий в каждой группе.
-сумма значений результативного признака; Mj – число предприятий в каждой группе.
Аналогичным образом по всей совокупности получим:
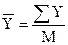 =
= 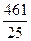 =18,44(шт.) .
=18,44(шт.) .
1.5.Построим расчетно-аналитическую групповую таблицу.
Зависимость производительности труда от энерговооруженности
| Группы предприятий по энерговооруженности, кВт.ч (Х) | Число предприятий в группе (Мj) | Средняя производительность труда, шт. ( 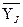 ) ) | ( 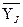 - - 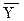 )2Мj )2Мj |
| 7,1-8,6 8,6-10,1 10,1-11,6 11,6-13,1 13,1-14,6 | 15,4 16,5 18,8 20,0 20,4 | 46,208 15,054 0,389 12,168 30,733 | |
| Итого | 18,4 | 104,552 |
2. Оценим тесноту связи между изучаемыми признаками с помощью эмпирического корреляционного отношения (методика расчета которого рассмотрена выше):
hэ = 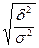 .
.
2.1. Предварительно рассчитываем общую дисперсию (s2), характеризующую вариацию результативного признака вследствие влияния всех действующих на него факторов,
d2 = 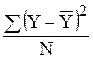 =
= 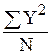 -
- 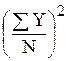 =
= 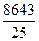 -18,442=345,720-340,034=5,684.
-18,442=345,720-340,034=5,684.
2.2. Рассчитаем межгрупповую дисперсию (d2) в соответствии с вышеизложенной методикой:
d2 = 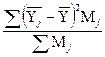 =
= 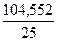 =4,18.
=4,18.
