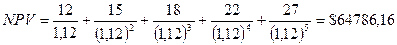Дисконтированная сумма не постоянной ренты

Однако, в международной практике эффективность инвестиционного проекта оценивается обычно не по будущей сумме, а по текущей сумме, пересчитанной к началу сделки, к моменту инвестиции.

Очевидно, что взнос в конце первого года С₁ дисконтируется к началу сделки как 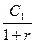; взнос в конце второго года С₂ дисконтируется к началу сделки как 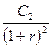и т.д. Взнос в конце k–ого года С_k дисконтируется как .

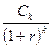Общая сумма дохода (или выплаченного долга), приведенная к началу сделки (к моменту инвестиции) определится как

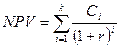. (3.2)

NPV (nеt present value – сеть текущих значений)

Эту величину называют чистым приведенным доходом финансовой сделки или чистым текущим объемом вклада. Ее сравнивают с первоначальной инвестицией PV. Если NPV>PV, то инвестиционный проект принесет прибыль на начальный момент больше затраченных денег, его принимают. В противном случае инвестиционный проект отвергается. В некоторых источниках [1] за чистый приведенный доход принимается разность D:

D=NPV – PV.

Если D>0 – проект приносит доход, он принимается. В противном случае – отвергается.

В Excel имеется функция НПЗ, высчитывающая чистый текущий объем вклада. Ее синтаксис:

НПЗ(ставка; 1-е знач.; 2-е знач.;…; 29-е знач.).

Здесь ставка – годовая процентная ставка;

1-е знач. 2-е знач. ··············

от 1 до 29 аргументов – выплаты, равномерно распределенные во времени и осуществляемые в конце периодов (выплаты могут быть не равны между собой и иметь разные знаки).

Если в начале первого года существует взнос C₀, то он не включается в число аргументов функции НПЗ, а прибавляется потом к функции.

В принятых здесь обозначениях

NPV=НПЗ(r; C₁; C₂;…; C_k) (k £ 29) (3.3)

Отметим еще раз, что эту формулу можно применять даже, если C_i имеют разные знаки, т.е. в какой–то год инвестиционный проект приносит убыток.

Пример 3.1

Вы решили заняться ресторанным бизнесом и оценили первоначальный взнос за аренду помещения, его ремонт и закупку оборудования в 50 тыс. долларов. Вы ожидаете получить доход:

В конце 1-ого года 12 тыс. долларов;

" 2-ого года 15 тыс. долларов;

" 3-его года 18 тыс. долларов;

" 4-ого года 22 тыс. долларов;

" 5-ого года 27 тыс. долларов.

Годовая процентная ставка банка r=12%. Оценим, “стоит ли игра свеч”, или выгоднее просто положить деньги в банк.

1) По формуле (3.1) будущий доход инвестиционного проекта   FVи=12´1,124+15´1,123+18´1,122+22´1,12+27 = $114 175,4 Если 50 тыс. долларов положить в банк, то через 5 лет накопится сумма FVБ=50´(1+0,12)5=$88 117,08 С точки зрения будущей суммы проект ресторанного бизнеса выгоден. 2) Оценим инвестиционный проект по сумме дохода, приведенной к началу инвестиции. По формуле (3.2)

Проверим этот инвестиционный проект с точки зрения будущего дохода и с точки зрения чистого приведенного дохода.

Решение.

PV = $ 50 тыс.

k = 5 лет.

r = 0,12

C₁ = $ 12 тыс.

C₂ = $ 15 тыс.

C₃ = $ 18 тыс.

C₄ = $ 22 тыс.

C₅ = $ 27 тыс.

FV_И = ? FV_Б =?

NPV = ?

Проверим этот расчет по формуле

НПЗ (0,12; 12; 15; 18; 22; 27) = $ 64786,16 – тот же результат.

Как видим, принесенный проектом доход, пересчитанный к моменту инвестиции, больше капитальных первоначальных вложений (PV=$ 50 тыс.). Ресторанный бизнес выгоднее вложения денег в банк.