Смешанная система счисления

КУРСОВАЯ РАБОТА

по дисциплине «Информационные технологии»

тема: Системы счисления.

Выполнил:

рядовой внутренней службы курсант 13 учебной группы Байкеев Макс Галимжанович

Руководитель курсовой работы

Подполковник внутренней службы Паринов А.В.

Защищена _________________ Оценка _________________

Воронеж - 2014 г.

Содержание

1. Системы счисления. Основные понятия. 2

1.2. Двоичная система счисления. 3

3. Смешанная система счисления. 5

3.1. Применение теоремы о смешанных системах счисления. 6

3.2 Перевод из одной системы счисления в другую и простейшие арифметические операции. Перевод целых чисел. 8

3.3. Перевод дробных чисел. 9

3.4. Перевод смешанных чисел. 10

4. Основные арифметические операции. 11

4.1. Сложение. 11

4.2. Вычитание. 13

4.3 Умножение. 14

4.4 Деление. 15

Список использованной литературы.. 15

Системы счисления

Система счисления - символический метод записи чисел, представление чисел с помощью письменных знаков.

Позиционные с/с – с/с, в которых величина, обозначаемая цифрой, зависит от позиции, в которой находится эта цифра.

Непозиционные с/с - с/с, в которых вес цифры не зависит от позиции, которую она занимает в числе.

Числа с фиксированной запятой (точкой) – естественная форма представления. Все числа представляются в виде последовательности с постоянным для всех чисел положением запятой, отделяющей целую часть от дробной.

Нормальная форма – числа с плавающей запятой (точкой).

Основание с/с - количество знаков или символов, используемых для изображения числа в данной системе счисления.

1.2. Двоичная система счисления Двоичная система счисления — это позиционная система счисления с основанием В этой систем запись числа в некоторой системе счисления называется кодом числа. Общий вид числа:

A = anan-1...a2a1a0 е счисления числа записываются с помощью двух символов (1 и 0).

Отдельную позицию в изображении числа принято называть разрядом, а номер позиции - номером разряда. Число разрядов в записи числа называется разрядностью и совпадает с его длиной.

Двоичная система счисления (Бинарная система счисления, binary) -- позиционная система счисления с основанием 2. Для представления чисел используются символы 0 и 1.

Пример:

100100112=1 × 27 + 0 × 26 + 0 × 25 + 1 × 24 + 0 × 23 + 0 × 22 + 1 × 21 + 1 × 20 = 14710

Соответствие первых двух десятков двоичной и десятичной систем счисления

Десятичная 0 1 2 3 4 5 6 7 8 9

Двоичная 0 1 10 11 100 101 110 111 1000 1001

Десятичная 10 11 12 13 14 15 16 17 18 19

Двоичная 1010 1011 1100 1101 1110 1111 10000 10001 10010 10011

Практическое применение двоичной системы затрудняется, во-первых, привычкой нашей к десятичной системе, приобретаемой с детства и, вероятно, отчасти унаследованной, и тем обстоятельством, что в двоичной системе для обозначения даже небольших чисел требуется гораздо большее число цифр, чем в десятичной. Так, например, 100 в десятичной системе будет изображаться 1100100 в двоичной, 1000 десятичной системы есть 1111101000 в двоичной и т. д.

Чтобы написать какое-нибудь число в двоичной системе, должно делить его последовательно на 2 и писать подряд, справа налево, остатки от деления. Например, чтобы написать 400 в двоичной системе, делим это число на 2, первое частное 200, остаток 0, второе частное 100, остаток 0, третье частное 5 0, остаток 0, четвертое частное 25, остаток 0, пятое частное 12, остаток 1, шестое частное 6, остаток 0, седьмое частное 3, остаток 0, восьмое частное 1, остаток 1, девятое и последнее частное 0, остаток 1, и так 400 десятичной системы пишется 110010000 в бинарной.

Переход от числа, написанного в двоичной системе, к десятичной, совершается простым сложением степеней числа 2, означенных в числе. Так, напр., число 110010000 в двоичной системе есть сумма 8-й, 7-й и 4-й степени двух, т. е. 256, 128 и 16, т. е. 400, ибо, как сказано выше, единицы на различных местах в написанном числе означают разные степени 2-х, которые вместе составляют данное число.

Смешанная система счисления

Смешанная система счисления является обобщением -ичной системы счисления и также зачастую относится к позиционным системам счисления. Основанием смешанной системы счисления является возрастающая последовательность чисел 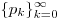и каждое число x представляется как линейная комбинация:

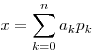
где на коэффициенты ak накладываются некоторые ограничения.

Записью числа z в смешанной системе счисления называется перечисление его цифр в порядке уменьшения индекса k, начиная с первого ненулевого.

Если 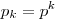для некоторого p, то смешанная система счисления совпадает с p-ичной системой счисления.

Наиболее известным примером смешанной системы счисления являются представление времени в виде количества суток, часов, минут и секунд. При этом величина d дней h часов m минут s секунд соответствует значению 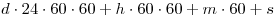секунд.