Построение непрерывного (интервального) вариационного ряда и его графическое изображение

При построении интервальных рядов распределения, прежде всего, устанавливают число групп (интервалов), на которые разбиваются все единицы изучаемой совокупности (см. тему сводка и группировка).

Величина интервала должна определяться в соответствии с точностью данных наблюдения.

Пример 2. Имеются данные о содержании дубильных веществ в 50 образцах черного байхового чая:

6,5	7,5	7,4	6,8	8,4
8,1	7,8	8,3	7,9	7,6
7,1	8,4	6,8	7,8	7,2
8,1	7,8	8,5
7,2	7,6	7,4	7,4	7,5
7,6	7,7	8,7	8,4	6,8
7,3	7,6	7,8	8,6	7,2
	7,9	7,8	8,6	7,8
7,6	6,5	8,9	8,5	8,2
	7,5	7,8	8,8	8,9

1. Постройте ряд распределения, разбив все данные на 6 групп с равными интервалами.

2. По данным ряда распределения вычислите среднее содержание дубильных веществ, среднее квадратическое отклонение и коэффициент вариации.

3. Укажите модальный интервал ряда распределения и моду.

4. Данные о содержании дубильных веществ в чае представьте на графике и сделать выводы.

Решение: Исходя, из заданного количества групп находим длину интервала.

Длина интервала (L) определяется по формуле:

L = R / n,

где R = X max – X min – размах вариации, при этом

X max – максимальное значение группировочного признака,

X min – минимальное значение группировочного признака.

L =(8,9-6,5)/6=0,4

Ряд распределения содержания дубильных веществ будет иметь следующий вид:

Содежание дубильных	6,5-6,9	6,9-7,3	7,3-7,7	7,7-8,1	8,1-8,5	8,5-8,9	Всего
веществ в %
Количество образцов
( ¦i ) - частоты

Среднее содержание дубильных веществ, среднее квадратическое отклонение и коэффициент вариации определяются соответственно по формулам:

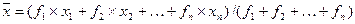, где

`х – средняя арифметическая взвешенная;

х₁, х₂, …, х_n – среднее содержание дубильных веществ в каждом из интервалов;

f₁, f₂, …, f_n – частоты, веса варьирующего признака.

`х =(6×6,7+7×7,1+12×7,5+13×7,9+6×8,3+6×8,7)/(6+7+12+13+6+6)=7,9(%)

Средняя квадратическая:

- Простая средняя квадратическая s=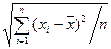

- Взвешенная средняя квадратическая s=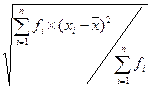

s – средняя квадратическая;

х_i – значение (варианты) некоторой совокупности, где i принимает значение от 1 до 6;

f_i - частота (вес) варьирующего признака (i = );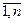

`х – средняя арифметическая (простая взвешенная);

s=(6×(6,7-7,9)²+7×(7,1-7,9)²+12×(7,5-7,9)²+13×(7,9-7,9)²+6×(8,3-7,9)²+6×(8,7-7,9)²)/ (6+7+12+13+6+6)=0,59(%)

Коэффициент вариации: V=(s/`х )×100%=(0,59/7,9)×100%=7,5(%)

Модальным интервалом будет интервал (7,7 – 8,1) как наиболее часто встречающийся в общем количестве образцов.

Для графического изображения интервальных вариационных рядов используется гистограмма. Она строится так: на оси абсцисс откладываются равные отрезки, которые в принятом масштабе соответствуют величине интервалов вариационного ряда. На отрезках строят прямоугольники, площади которых пропорциональны частотам (или частостям) интервала.

Гистограмма ряда распределения содержания дубильных веществ в нашем частном случае будет иметь следующий вид:

количество

образцов (¦i)

Гистограмма может быть преобразована в полигон распределения, если середина верхних сторон прямоугольников соединить отрезками прямых. Две крайние точки прямоугольников замыкаются на оси абсцисс, на середине интервалов, в которых частоты (частности) равны нулю.

Мода определяется по гистограмме распределения. Для этого правую вершину модального прямоугольника соединяем с правым верхним углом предыдущего прямоугольника, а левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Абсцисс точки пересечения этих прямых и будет модой распределения.

Коэффициент вариации V=7,5(%) показывает, что средняя величина является характерной характеристикой исследуемого ряда. Модальная величина, полученная графически, отличается от средней арифметической взвешенной величины.